こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
インプット(計画)よりもアウトプット(行動)が大事だ、とはよく言われますが、これは公務員試験の勉強にも当てはまる考え方だと思うんです。
参考書を一冊仕上げたら、すぐに過去問を見たほうがいいと思います。
過去問を見てみると、意外と出題分野に偏りがあるので、力の入れどころが分かってきます。
あなたが今、参考書で苦労している分野も、実は出題率が低くてあまり対策が必要ないところかもしれません。
過去問は早めに見ておくことをおすすめします。
前回は、新幹線の座席の位置関係を確定させる問題をやりましたね。
国家総合職で頻出の、位置関係をテーマにした問題なので、解いてない方はぜひ挑戦してみてください。
すでに解いた方は、大まかにでいいので解法の手順を脳内で再現してみましょう。
思い出せない方は、早めに解説を見返しておくことをおすすめします。
思い出すたびに、記憶が強固になっていきます。
そうした記憶の積み重ねが、数的処理の得点アップにつながるので、問題を解いたら復習も忘れずに行いましょう!
復習がバッチリな方は、本日の問題へ参ります。
本日の演習問題
高さの異なる4本のビルが、図のように一直線上に等間隔で並んで建っている。このうち、両端の2本には地上から屋上まで通じるエレベーターがあり、昇降しながら外を見渡せる造りになっている。ビルの高さとエレベーターから見た景色について、次のことが分かっている。
- エレベーターはそれぞれ一定の速さで地上と屋上の間を止まることなく行き来している。
- ビルiとビルivのエレベーターの速さの比は9:4である。
- ビルivの高さはビルiiiの高さの2倍である。
- ビルivにおいて地上からエレベーターで上昇すると、地上からビルivの高さの\(\frac{1}{3}\)の地点を通過するときに、ビルiの屋上が見え始める。
- ビルivの屋上からビルiを見ると、地上から高さ6の階層まで見える。
いま、ビルiの屋上にいるAとビルivの1階にいるBが、同時にエレベーターに乗り昇降を繰り返すことを考える。このとき、AとBが初めて同じ高さにいる互いの姿を見るのは、Aの乗るエレベーターがビルiの高さの何倍の地点を通過するときか。
ただし、ビルの幅やAとBの身長、およびエレベーターの大きさは考慮しないものとする。

- \(\frac{1}{2}\)
- \(\frac{3}{5}\)
- \(\frac{7}{10}\)
- \(\frac{4}{5}\)
- \(\frac{9}{10}\)
4
ビルの昇降と高さの問題です。
分かっていることの項目でビルivが頻繁に登場するので、ビルivを主軸に考えるのがよさそうですね。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
分かっていることの3つ目、「ビルivの高さはビルiiiの高さの2倍」より、ビルiiiの高さを\(h\)とすれば、ビルivの高さは\(2h\)と表せます。
すると、分かっていることの4つ目、「ビルivにおいて地上からエレベーターで上昇すると、地上からビルivの高さの(\frac{1}{3})の地点を通過するときに、ビルiの屋上が見え始めた」より、ビルivにおける高さ\(\frac{2}{3}h\)の地点とビルiの屋上を結んだ一直線上には、ビルiiおよびビルiiiの屋上が並ぶことになります。
言語化すると分かりづらいですが、図で表すと次のようになります。
百聞は一見にしかずですね。
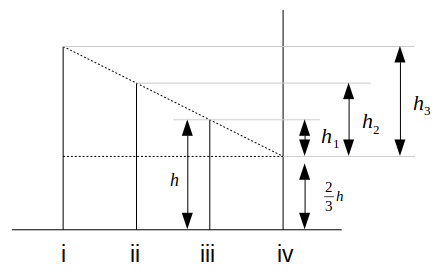
この図のように\(h_1, h_2, h_3\)を設定すると、まず\(h_1=\frac{h}{3}\)です。
次に\(h_2\)について、ビルが等間隔に建っていることと三角形の相似より、\(h_1:h_2=1:2\)
これより、\(h_2=\frac{2}{3}h\)
同様に、\(h_1:h_3=1:3\)より、\(h_3=h\)
以上から、ビルi〜ivの高さを\(h\)で表すと次のようになります。
| i | ii | iii | iv | |
| 高さ | \(\frac{5}{3}h\) | \(\frac{4}{3}h\) | \(h\) | \(2h\) |
次に、分かっていることの5つ目「ビルivの屋上からビルiを見ると、地上から高さ6の階層まで見える」を使いましょう。
図で表すと次のようになります。
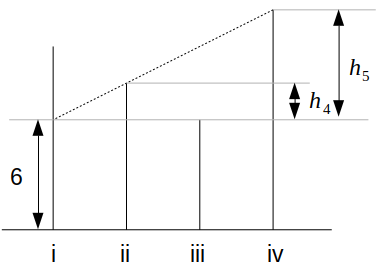
先ほどの表によると、\(h_4=\frac{4}{3}h-6\)、\(h_5=2h-6\)
また、三角形の相似より、\(h_4:h_5=1:3\)なので、\(h=6\)と求められます。
これにより、各ビルの高さが具体的な数値として次のように決まります。
| i | ii | iii | iv | |
| 高さ | 10 | 8 | 6 | 12 |
これをもとに、AとBが同じ高さを通過する瞬間について考察します。
まず、AとBの高さが最初に一致するのはいつでしょう?
Aは屋上から、Bは1階から互いに逆向きに進むことを考えると、2人の高さが一致するのは、2人の昇った(降りた)距離の合計がビルiの高さに等しいときですね。
AとBの進む速さは、比例定数\(k\)を用いると、それぞれ\(9k\)、\(4k\)と表せます。
さらに、最初に同じ高さを通過するまでの時間を\(t_1\)とすると、
\[
9kt_1+4kt_1=10 ∴kt_1=\frac{10}{13}
\]
このとき、Bの高さは\(4kt_1=\frac{40}{13}<4\)
よって、この瞬間にBからはビルiが全く見えない状態で、当然Aの姿も見えません。
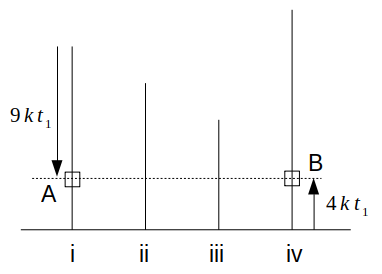
ここから次にAとBが同じ高さを通過する場合は、もっと簡単に考えることができます。
AとBの進む速さが9:4であることより、例えばBが4だけ上昇したとき、Aは屋上から9だけ下降した位置にいます(\(t_1\)の少しあと)。
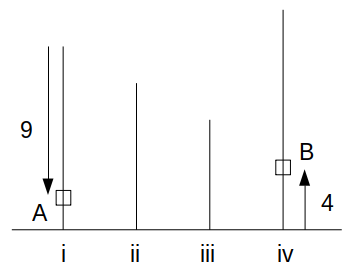
同様に、Bが8だけ上昇したときは、Aの移動量は18で、Aはビルiの1階で折り返して8だけ上昇することになります。
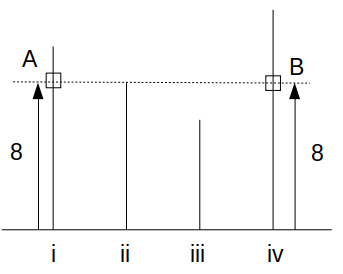
このとき、AとBは初めて同じ高さにいる互いの姿を見ることになります。
ビルiの高さは10なので、このときのAの位置はビルiの高さの\(\frac{8}{10}=\frac{4}{5}\)倍ですね。
したがって、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
平面図形に速さの要素が混ざったような問題でした。
前半は、相似の関係を利用してビルの高さを求めていくことになります。
始めにビルiiiの高さを\(3h\)とおけば、分数が出てこなくなるのでちょっと楽かもしれません。
ただ、初見でそこまで見越して文字を導入できる人は少ないだろうと思ったので、解説では単純に\(h\)とおいて進めました。
市販の問題集では、そうやって分数が出ないように文字を設定しているのをよく見かけますが、正直そんなに要領良く立ち回れる人なんてそうはいないと思います。
少なくとも私はできませんでした。
多少泥臭くなったとしても、正解にたどり着ければOKなので、解説はあくまで参考程度に見ておきましょう。
後半は速さの考え方を応用し、AとBが同じ高さになるときのAの位置を求めます。
「出会う」や「追いつく」といった出来事を数式にするとどうなるのか、きちんと整理して頭に入れておきましょう。
平面図形と速さは、どちらも国家総合職では出題されやすいテーマになっています。
今回のように複合的な問題の場合でも、基本にある考え方は同じなので、簡単な問題もおろそかにせず、道具として使いこなせるまで練習しましょう。
本サイトで過去に紹介した速さの問題も参考になると思うので、まだの方は挑戦してみてください↓
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
「ビルivの高さはビルiiiの高さの2倍」より、ビルiiiの高さを\(h\)とすると、ビルivの高さは\(2h\)である。
「ビルivにおいて地上からエレベーターで上昇すると、地上からビルivの高さの\(\frac{1}{3}\)の地点を通過するときに、ビルiの屋上が見え始めた」を図示すると、次のようになる。
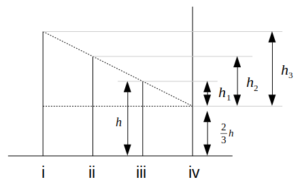
hをもとにビルの高さを求める
この図のように\(h_1, h_2, h_3\)を設定すると、まず、\(h_1=\frac{h}{3}\)
次に\(h_2\)について、ビルが等間隔に建っていることと三角形の相似より、\(h_1:h_2=1:2\)
これより、\(h_2=\frac{2}{3}h\)
同様に、\(h_1:h_3=1:3\)より、\(h_3=h\)
以上から、ビルi〜ivの高さを\(h\)で表したものをまとめると以下のようになる。
| i | ii | iii | iv | |
| 高さ | \(\frac{5}{3}h\) | \(\frac{4}{3}h\) | \(h\) | \(2h\) |
次に、「ビルivの屋上からビルiを見ると、地上から高さ6の階層まで見える」を図で表すと次のようになる。
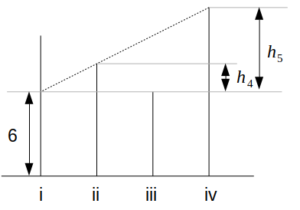
ivの屋上から見える高さ
ここで、\(h_4=\frac{4}{3}h-6\)、\(h_5=2h-6\)
また、三角形の相似より、\(h_4:h_5=1:3\)であるから、\(h=6\)。
これにより、各ビルの高さを数値化したものは以下のようになる。
| i | ii | iii | iv | |
| 高さ | 10 | 8 | 6 | 12 |
これをもとに、AとBが同じ高さを通過する瞬間について考察する。
まず、AとBの高さが最初に一致する瞬間を考える。
Aは屋上から、Bは1階から互いに逆向きに進むので、2人の高さが一致するのは、2人の昇った(降りた)距離の合計がビルiの高さに等しいときである。
AとBの進む速さは、比例定数\(k\)を用いてそれぞれ\(9k\)、\(4k\)と表せる。
さらに、最初に同じ高さを通過するまでの時間を\(t_1\)とすると、
\[
9kt_1+4kt_1=10 ∴kt_1=\frac{10}{13}
\]
このとき、Bの高さは\(4kt_1=\frac{40}{13}<4\)であるから、BはAの姿を見ることはできない。
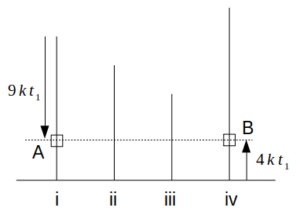
AとBの高さが初めて一致するとき
続いて、2回目にAとBの高さが一致するのは、AとBの速さの比が9:4であることから、Bが8だけ上昇したときである。
このとき、Aも高さ8の位置におり、両者は初めて同じ高さにいる互いの姿を見ることになる。
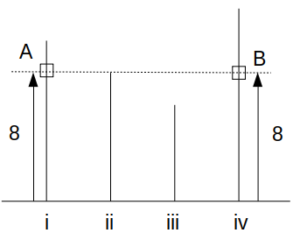
AとBの高さが2回目に一致するとき
ビルiの高さは10なので、このときのAの位置はビルiの高さの\(\frac{8}{10}=\frac{4}{5}\)倍である。
したがって、正解は4である。

コメント