こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「??」
箸休め的なゆるい回です。
よって、今回は「解法のポイント」はありません。
…というのはウソ。

ウソなんかい
既知の解き方と結びつけて理解する
解法、というよりは勉強のコツです。
ぜひ普段の学習に活かしてください。
演習問題:彗星の周期性
彗星の中には、楕円形の公転軌道を持ち、特定の周期で観測されるものがある。彗星の周期をXとしたとき、[X]※=15なる彗星(\(C_{15}\)とする)、および[X]※=19なる彗星(\(C_{19}\)とする)はそれぞれ9種類、4種類存在することが分かっている。これらの彗星は必ず一定の周期で現れ、かつ同年内に消滅するものとする。また、1年のうちに現れる彗星は、\(C_{15}\)および\(C_{19}\)でそれぞれ1種類ずつのみであるとする。すなわち、同じ年に2種類以上の\(C_{15}\)(または\(C_{19}\))が現れることはないが、\(C_{15}\)および\(C_{19}\)が1種類ずつ現れることはあり得る。
いま、2024年以降に初めて\(C_{15}\)および\(C_{19}\)が現れる年は次の通りであるとする。
\(C_{15}\):2024年、2027年、2028年、2032年〜2037年の各年
\(C_{19}\):2027年、2030年、2031年、2033年
2024年〜2323年の300年間に、\(C_{19}\)のみが現れる年はいくつあるかを次のように考えたとき、空欄に当てはまるものの組み合わせとして正しいのはどれか。
「\(C_{19}\)は各種それぞれ19年に1回ずつ現れるから、2024年〜2323年の300年間に\(C_{19}\)のいずれかが現れる年は『 A 』回ある。一方、\(C_{15}\)のある種類と\(C_{19}\)のある種類がともに現れる年は種類ごとに285(=15×19)年に1回であるから、2024年〜2323年の間に\(C_{15}\)と\(C_{19}\)がともに現れる年は全部で『 B 』回ある。よって、\(C_{19}\)のみが現れる年は『 C 』回である。」
※[X]は、Xを超えない最大の整数を表す。
例:[15.8]=15
| A | B | C | |
| 1. | 60 | 36 | 24 |
| 2. | 60 | 38 | 22 |
| 3. | 64 | 38 | 22 |
| 4. | 64 | 38 | 18 |
| 5. | 64 | 40 | 18 |
3
彗星の周期性をテーマにした問題。
空欄を一つずつ埋めていきます。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:割り算で数えて共通部分を引く
問題文の空欄を一つずつ埋めていきます。
「\(C_{19}\)から『\(C_{15}\)かつ\(C_{19}\)』を引くことで、\(C_{19}\)のみの年を数える」
というのが全体の流れです。

ベン図にするとこんな感じ↓
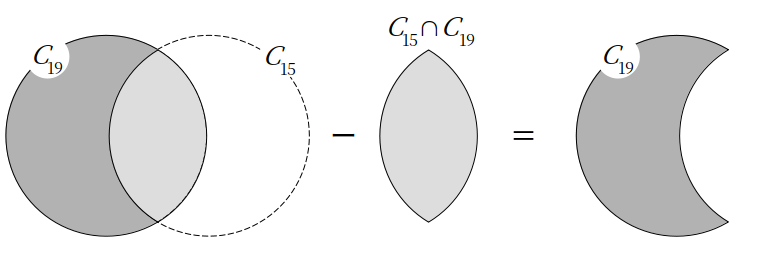
A:19年周期の回数×種類
\(C_{19}\)は19年周期で現れるので、300年の中に19年のカタマリがいくつ入るかを数えます。
つまり、割り算です。
300÷19=15…15
これより、\(C_{19}\)は種類ごとに15回現れます。
\(C_{19}\)は4種類あるので、いずれかが現れる年は
15×4=60より、300年間に60回
…とするのは【誤り】です。
結論から言うと、正しくは
(15+1)×4=64(回)……A
次の図を見てください。
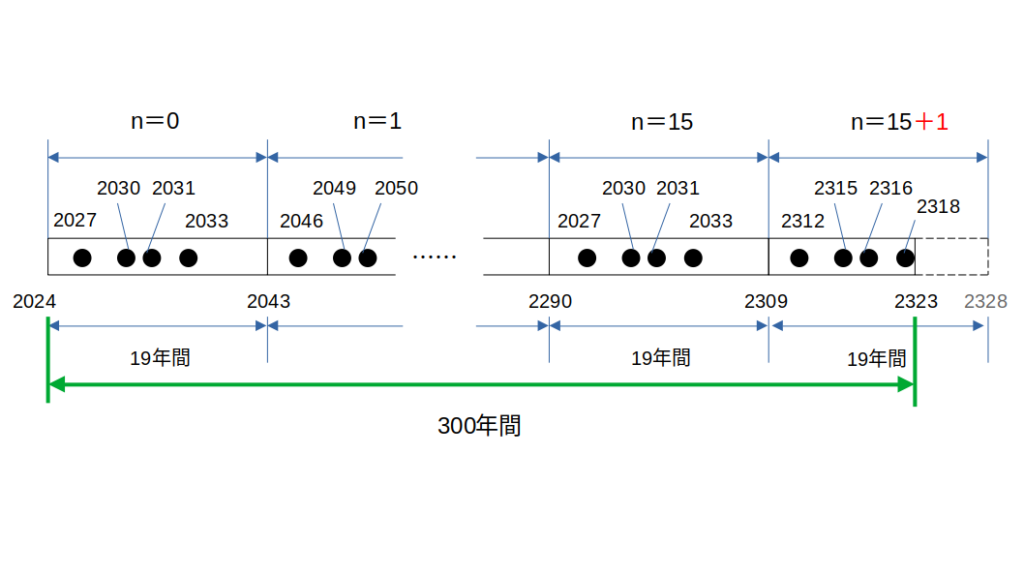
この図では、\(C_19\)が現れる年を、次のように整数\(n\)を使って表しています。
\[
2027+19n \\
2030+19n \\
2031+19n \\
2033+19n
\]
余りの扱いがミソ。
実は、300÷19の商「15(回)」にはこの「余り」がカウントされていません。
なので、\(C_{19}\)が現れる回数は、余りの1ブロックを追加した16回(1種類あたり)となります。
これは4種類全てに当てはまるので、(15+1)を4倍して64回です。
小学校で習う「ベンチの問題」を思い出してください。

「10人がけのベンチに32人が座るとき、ベンチはいくつ必要か?」ってやつね
この場合、3脚(=32÷10の商)だと2人が座れません。
あぶれた2人のためのベンチが必要なので、(3+1)脚が答えになりますね。
本問も、考え方はこれと同じ。
前に見た簡単な問題に結びつけて理解する、というのをやってくと、初見の問題に対処する力が付いてきます。
どこかの記事でも触れましたが、めっちゃ大事なことなので「解法のポイント」としておきます。
既知の解き方と結びつけて理解する
B:300年→(15+285)年と考える
次に、
“\(C_{15}\)のある種類と\(C_{19}\)のある種類がともに現れる年は種類ごとに285(=15×19)年に1回”
について。
これは、\(C_{15}\)と\(C_{19}\)のある一組が285年周期で現れることを述べてます。
もう少し詳しくいうと、\(C_{15}\)と\(C_{19}\)の特定の組み合わせが同時に現れるのは、285年のうちに1回のみである、ということです。
このことを利用し、2024年〜2323年の300年間を次のような2区間に分割して考えます。
(i)2024年〜2038年
(ii)2039年〜2323年
(15+285)年という分け方がミソ。
285年の区間では、\(C_{15}\)と\(C_{19}\)のペアは1回ずつしか現れない(=285年周期)ため、組み合わせのパターン数がそのまま回数となります。
こうすると、組み合わせの考え方で機械的にカウントできるわけです。

(i)の15年間は直接数えればいい
(i)2024年〜2038年:直接数える
「2024年以降に初めて〜」の箇所を見ればOK。
\(C_{15}\):2024年、2027年、2028年、2032年〜2037年の各年
\(C_{19}\):2027年、2030年、2031年、2033年
これによると、この区間で\(C_{15}\)と\(C_{19}\)が同時に現れる年は2回。

2027年と2033年ね
(ii)2039年〜2323年:組み合わせを数える
すでに述べた通り、この区間では\(C_{15}\)と\(C_{19}\)の組み合わせの数を数えればOK。
それぞれ9種類、4種類あるので、9×4=36回
2024年〜2323年では、2+36=38(回)……B
C:全体から共通部分を引く
冒頭で述べた通り、\(C_{19}\)全体から「\(C_{15}\)と\(C_{19}\)の年」を引きます。
つまり、AーB=60ー38=22(回)……C
以上より、3が正解です。
おわりに:過去に見た解き方と関連付ける
お疲れ様でした!
問題演習で解説を読むときは、
「過去に見た解き方と関連付けられないか?」
という点に注意を向けてみてください。
偉そうに言ってるけど、途中で思いついて後付けしただけです。

正直でよろしい
今回は彗星が現れる回数を、誘導にしたがって数える問題でした。
集合論的な考え方をベースに、個々の空欄は周期性に基づいて考える必要があります。
誘導にしたがえばOK。
問題文が近年まれに見るほど長ったらしいのは仕様です。

これでも元ネタよりは少ないのよ
悲しいときー懇親会で持ち帰ったビンゴの紙を家で捨てるときー

昨日会社の懇親会がありました
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
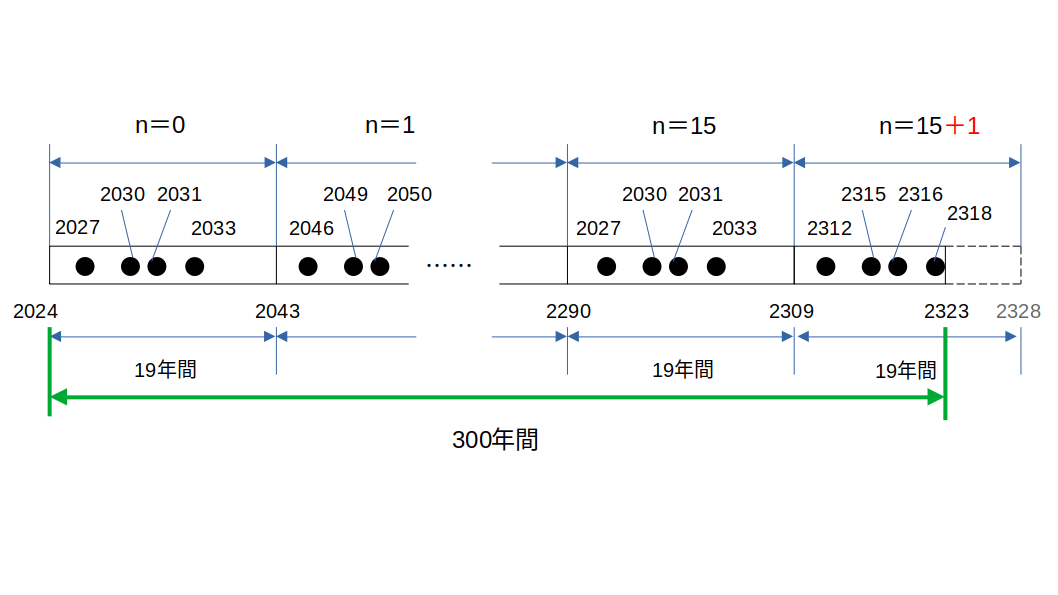
C19が現れる回数は商+1
図では、\(C_19\)が現れる年を、次のように整数\(n\)を使って表している。
\[
2027+19n \\
2030+19n \\
2031+19n \\
2033+19n
\]
図のように、\(C_{19}\)は種類ごとに15+1回現れる。
\(C_{19}\)は4種類あるから、いずれかが現れる年は
(15+1)×4=64(回)……A
次に、\(C_{15}\)と\(C_{19}\)の特定の組み合わせが同時に現れるのは、285年のうちに1回のみである。
よって、2039年〜2323年の285年間に\(C_{15}\)と\(C_{19}\)が同時に現れる回数は、\(C_{15}\)と\(C_{19}\)のペアの総数に等しく、9種類×4種類=36回
さらに、2024年〜2038年では\(C_{15}\)と\(C_{19}\)が同時に現れる年は2027年と2033年の2回ある。
よって、2024年〜2323年では、2+36=38(回)……B
\(C_{19}\)のみの年の回数は、\(C_{19}\)から「\(C_{15}\)かつ\(C_{19}\)」を引けばよい。
つまり、AーB=60ー38=22(回)……C
よって、3が正解である。



コメント
Aの値を考える場合は 300÷15=15…15 ←の余り(15)の部分に注意する必要があります。
2027年のC19が現れる年は 2027+19n (nは0以上の整数)と表記でき
nに15を入れると 2027+19×15=2312 となり 2024年~2323年までに16回現れます
2033のC19も 2033+19×15=2318 となり16回現れます
よってAの値は 4×15+4=64になります
要するに余りの15年間の間にもう一回現れる事があると言うことです
2024年~2038年までに現れるC19が余りの年数の間にもう一回現れます
上の
「Aの値を考える場合は 300÷15=15…15」 は
「Aの値を考える場合は 300÷19=15…15」 の間違いです
今回もご指摘ありがとうございます!
余りの扱いは盲点でした。
昔習った「ベンチの問題」と同じですね。
おかげさまで中身のある記事ができました。
大変勉強になり、感謝いたします。