こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
今回のテーマは「確率」です。
確率(&場合の数)の解き方は、以前紹介しました。
数的処理の対策をしたい方は必見です。
演習問題:特定の一人がトーナメントで優勝する確率
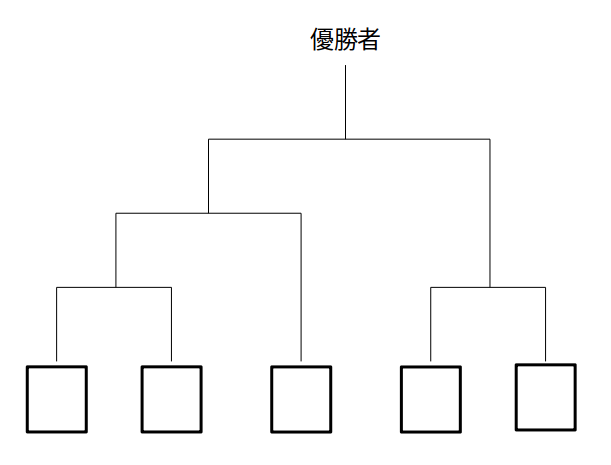
図のようなトーナメント方式で行われるじゃんけんの大会に、A〜Eの5人が参加した。トーナメント表における参加者の配置は、くじ引きにより無作為に決められる。このとき、あいこも含め全5回のじゃんけんの結果、Aが優勝する確率はいくらか。
ただし、A〜Eはいずれも等しい確率でグー、チョキ、パーを出すものとする。
- \(\frac{16}{243}\)
- \(\frac{32}{729}\)
- \(\frac{64}{729}\)
- \(\frac{64}{1215}\)
- \(\frac{128}{1215}\)
4
トーナメント戦の確率の問題です。
参加者の配置がランダムなのがややこしい。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下の略解を読んでね。
それでは、解説スタート!
解説:場合分けして確率の定義を使う
確率問題の「解法のポイント」をおさらい。
-
事象をカウントし定義から求めるやり方
- 樹形図や書き出しによる数え上げ
- 組み合わせや順列を使った計算
-
確率から確率を求めるやり方
- 排反事象の足し算(和の法則)
- 独立事象のかけ算(積の法則)
- 全体から引く(余事象の確率)
「定義」か?「確率から確率」か?
まず考えることは、「定義を使うか?」「確率から確率を求めるか?」です。
本問は各試行について具体的な確率が与えられているわけではないので、定義を使うしかありません。

「いずれも等しい確率で〜」のところは、あくまで「同様に確からしい」という補足説明
加えて、本問は5人いる参加者の配置が決まっていません。
配置のパターンだけでも5!=120通りあり、そこから各5試合で「勝ち」「負け」「あいこ」の分岐があります。
……さすがに数え上げられる気がしませんね。
そこで、本問は【2】の「組み合わせや順列による計算」で解いてみます。

途中で補助的に和・積の法則を使うことはあるけどね
確率の分母:全事象は何通り?
まず、トーナメントの配置は5!=120通り。
配置を一つに決めてしまうと、全5回の試合で「勝ち」「負け」「あいこ」の3通りのパターンがあります。
よって、試合の結果は全部で\(3^5=243\)通り

「勝ち」「負け」「あいこ」の、同じものを含む順列ね
これより、全事象は120×243通りとなります。
全事象数が分かったら、次は「全5回のじゃんけんの結果、Aが優勝する」パターンを数え上げます。
Aの配置で場合分け
本問は「Aが優勝する確率」を問うています。
なので、ここからはAの配置を決めないことには先に進めません。
注意すべきなのは、5つある配置は等価ではない、ということです。
具体的には、「一」または「二」、「三」、「四」または「五」で状況が異なります。

Aの試合数が変わるから、別々に考えないとダメなんです
そこで、以下ではAの配置が(i)「一」または「二」、(ii)「三」、(iii)「四」または「五」のときで場合分けして検討します。
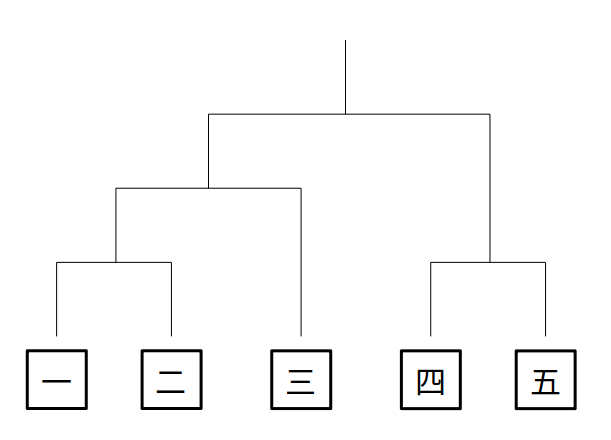
(i)Aが「一」または「二」のときの場合の数
Aの配置を「一」(または「二」)に固定したとき、残りの参加者の配置パターンは4!通り。
説明の都合上、配置を次のように仮定します。
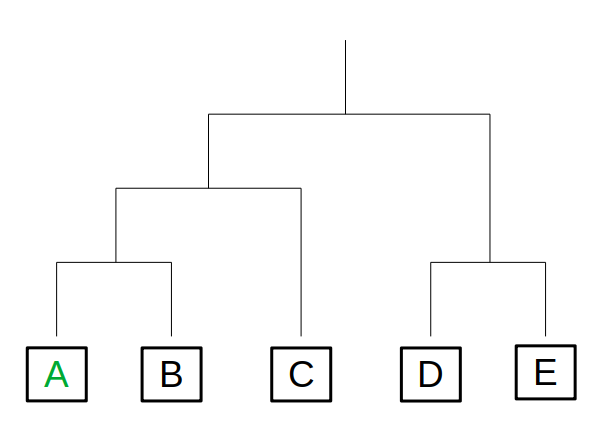
勝敗については、簡単のため、あいこが一度もなかった場合から考えます。
トーナメント表の左半分は、2試合ともAが勝つので1通り。
右半分はDが勝つケースとEが勝つケースの2通り。
決勝戦はAが勝つので、Aが優勝する場合の対戦パターンは1×2=2通りです。
次に、あいこがある場合を考えます。
1回だけあいこになる場合、どの試合であいこになるかが4通りあります。

試合は最短で4回だから、全5回ならあいこは1回
よって、あいこがある場合にAが優勝する場合の数は、2×4=8通り。
以上より、(i)の場合の数は、全部で8×4!通り。
(ii)Aが「三」のときの場合の数
Aの配置を「三」に固定したとき、残りの参加者の配置パターンは4!通り。
以下、次のような配置を仮定して進めます。
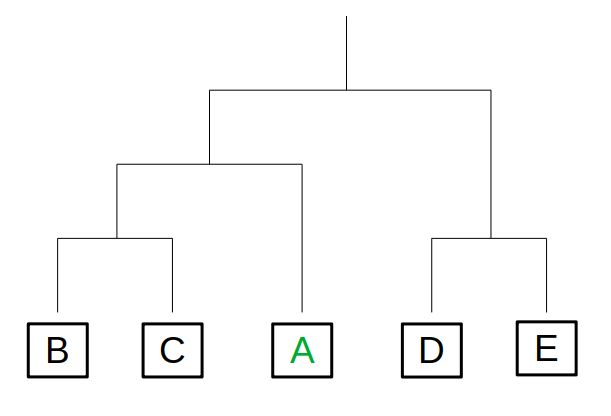
勝敗について、同じくあいこが一度もない状況から考えます。
トーナメント表の左半分では、第2回戦に上がってくるのがBなのかCなのかで2通りあります。
また右半分では、決勝戦に上がってくるのがDなのかEなのかで2通り。
よって、Aが優勝する場合の対戦パターンは2×2=4通りです。
あいこがある場合、どの試合であいこになるかが4通りあります。
よって、Aが優勝するケースは4×4=16通りです。
以上より、(ii)の場合の数は16×4!通りとなります。
(iii)Aが「四」または「五」のときの場合の数
Aの配置を「四」(または「五」)に固定したとき、残りの参加者の配置パターンは4!通り。
次のように配置を仮定します。
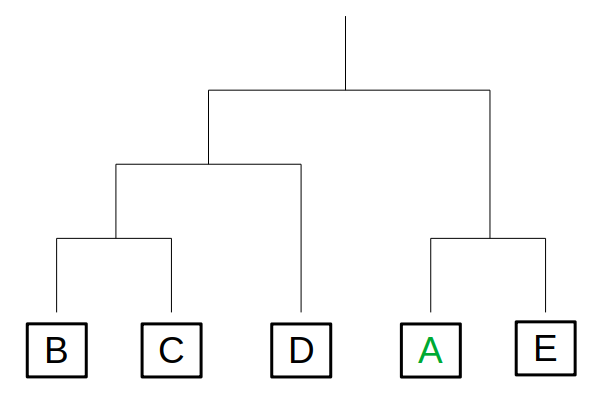
やはり、あいこが一度もない状況から考えます。
トーナメント表の左半分は、誰が勝ち上がってもOKです。
勝者のパターンは以下の4通り。
| 第1試合 | 第2試合 |
| B | B |
| B | D |
| C | C |
| C | D |
右半分は、Aが勝つので1通りです。
よって、対戦パターンは1×4=4通り。
どの試合であいこになるかが4通りなので、Aが優勝するケースは4×4=16通り。
以上より、(iii)の場合の数は16×4!通り。
(i)、(ii)、(iii)は同時に起こらない(=互いに排反)ので、確率は
\[
\frac{8×4!×2+16×4!+16×4!×2}{5!×243}=\frac{64}{1215}
\]
よって、4が正解です。
おわりに:確率の解法5つを使いこなす
お疲れ様でした!
確率で大切なのは、適切な解法を選ぶこと。
基本は「解法のポイント」にある5つで、このうちのいずれか一つ、あるいは複数を使って解きます。
今回は、トーナメントで特定の人が優勝する確率を求める問題でした。
全事象と「Aが優勝する事象」の場合の数を別々にカウントし、定義を使います。
対称性を利用して手際よく場合分けするのがポイント。
同じく確率を扱った問題をもう一つ。
「行けたら行く」って人がほんとに来る確率
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
トーナメントの配置パターンは5!=120通り。
各々の配置では、「勝ち」「負け」「あいこ」の3通りが全5試合あり、勝敗のパターンは全部で\(3^5=243\)通り。
これより、全事象は120×243通り。
以下、Aの配置が(i)「一」または「二」、(ii)「三」、(iii)「四」または「五」のときで場合分けし、Aが優勝する場合の数をカウントする。

漢数字で区別
(i)Aが「一」または「二」のとき
A以外の参加者の配置パターンは4!通り。
簡単のため、次図のケースであいこが一度もないパターンを考える

Aが「一」または「二」の場合
このとき、トーナメント表の左半分は、2試合ともAが勝つので1通り。
右半分はDが勝つケースとEが勝つケースの2通り。
決勝戦はAが勝つので、Aが優勝する場合の対戦パターンは1×2=2通り。
ここにあいこが1回だけ加わる場合、どの試合であいこになるかが4通り。
よって、あいこがある場合にAが優勝する場合の数は、2×4=8通り。
以上より、(i)の場合の数は、全部で8×4!通り。
(ii)Aが「三」のとき
A以外の参加者の配置パターンは4!通り。
以下、次図のような配置であいこが一度もないケースを仮定。

Aが「三」の場合
トーナメント表の左半分では、第2回戦に上がってくるのがBなのかCなのかで2通り。
右半分では、決勝戦に上がってくるのがDなのかEなのかで2通り。
よって、Aが優勝する場合の対戦パターンは2×2=4通り。
あいこがある場合、どの試合であいこになるかが4通りだから、Aが優勝するケースは4×4=16通り。
以上より、(ii)の場合の数は16×4!通り。
(iii)Aが「四」または「五」のとき
A以外の参加者の配置パターンは4!通り。
以下、次図のような配置であいこが一度もないケースを仮定。

Aが「四」または「五」の場合
トーナメント表の左半分について、勝者のパターンは以下の4通り。
| 第1試合 | 第2試合 |
| B | B |
| B | D |
| C | C |
| C | D |
右半分は、Aが勝つ1通りだけだから、対戦パターンは1×4=4通り。
どの試合であいこになるかが4通りだから、Aが優勝するケースは4×4=16通り。
以上より、(iii)の場合の数は16×4!通り。
(i)、(ii)、(iii)は互いに排反だから、確率は
\[
\frac{8×4!×2+16×4!+16×4!×2}{5!×243}=\frac{64}{1215}
\]
よって、4が正解である。

コメント