こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
残念(?)なお知らせですが、これからしばらく本サイトの更新頻度が毎日から隔日のペースになりそうです。
毎日更新できないのは口惜しいですが、記事の質を落とすよりはマシかな、と。
できる限り1日1記事の投稿を目指しますが、今後どうしても更新できない日が出てしまうこと、ご了承ください。
前回は、6回の試験の結果に基づく順位付けの問題をやりましたね。
国家総合職で毎年出題のある、対応関係の問題なので、解いてない方はぜひ挑戦してみてください。
もう解いた方は、忘れないよう定期的に復習しましょう。
せっかく新しい問題を解いたなら、確実に自分の糧にしたいですよね。
過去問レベルの問題演習をする段階でも、解いた問題から学べることはたくさんあると思います。
これからの問題演習で、そうした学びを積み上げていけば、必ず試験はパスできます。
そのためには、問題一つ一つに関する記憶を定着させていく必要があるのです。
だからこそ、勉強した内容を定期的に振り返ることが重要となります。
新しい問題を解くのに比べると、復習は面倒に思われるかもしれませんが、日々の勉強を無駄にしないためにも、欠かさず取り組みましょう!
復習がバッチリな方は、本日の問題へ参ります。
本日の演習問題
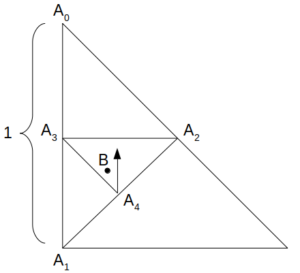
平面上に、直角をはさむ二辺の長さが1である直角二等辺三角形がある。いま、この三角形の頂点\(\mathrm{A_0}\)に十分な長さの針金の一端を固定し、次のような手順によって定まる点\(\mathrm{A_n}\)をなぞるように折り曲げていく。
まず、直角二等辺三角形の一辺に沿って\(\mathrm{A_0}\)から\(\mathrm{A_1}\)へと進む。そこから三角形の対辺へ下ろした垂線の足を\(\mathrm{A_2}\)として、今度は\(\mathrm{A_1}\)から\(\mathrm{A_2}\)へと進む。さらにそこから、線分\(\mathrm{A_1}\mathrm{A_2}\)を一辺とする直角二等辺三角形の対辺へ下ろした垂線の足を\(\mathrm{A_3}\)として、今度は\(\mathrm{A_2}\)から\(\mathrm{A_3}\)へと進む。これを繰り返したところ、針金のもう一方の端が直角二等辺三角形の内部の点Bに限りなく近づいた。このとき用いた針金の長さはいくらか。
ただし、針金の太さは無視できるものとする。
- \(1+\sqrt{2}\)
- \(2+\sqrt{2}\)
- \(2+2\sqrt{2}\)
- \(3+2\sqrt{2}\)
- \(5+\sqrt{2}\)
2
垂線をたどる針金の長さを求める問題です。
使う針金の長さはどのように変化していくのか、順を追って明らかにしてみましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
繰り返しの操作が絡む問題では、ステップごとの変化の規則性を問うている場合が多いです。
そこで、まずはステップごとの針金の長さの変化を見て、そこに規則性があるかどうか検討してみることにしましょう。
以下、線分\(\mathrm{A_0}\mathrm{A_1}\)、\(\mathrm{A_1}\mathrm{A_2}\)、\(\mathrm{A_2}\mathrm{A_3}\)、……の長さをそれぞれ\(L_1\)、\(L_2\)、\(L_3\)、……とおき、針金の全長を\(L\)とします。
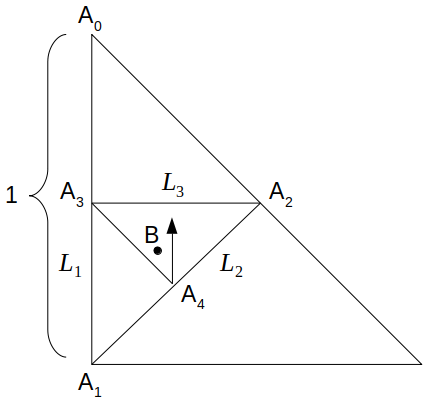
まず、\(L_1=1\)なので、\(L=1\)
次に、\(L_2\)について、△\(\mathrm{A_0}\mathrm{A_1}\mathrm{A_2}\)が直角二等辺三角形であることより、\(L_2=\frac{\sqrt{2}}{2}\)
よって、\(L=L_1+L_2=1+\frac{\sqrt{2}}{2}\)
また、\(L_3\)について、同じく△\(\mathrm{A_1}\mathrm{A_2}\mathrm{A_3}\)が直角二等辺三角形なので、\(L_3=\frac{\sqrt{2}}{2}L_2=\frac{1}{2}\)
よって、\(L=L_1+L_2+L_3=1+\frac{\sqrt{2}}{2}+\frac{1}{2}=\frac{3+\sqrt{2}}{2}\)
さらに、\(L_4\)について、やはり△\(\mathrm{A_2}\mathrm{A_3}\mathrm{A_4}\)が直角二等辺三角形なので、\(L_4=\frac{\sqrt{2}}{2}L_3=\frac{\sqrt{2}}{4}\)
よって、\(L=L_1+L_2+L_3+L_4=1+\frac{\sqrt{2}}{2}+\frac{1}{2}+\frac{\sqrt{2}}{4}=\frac{6+3\sqrt{2}}{4}\)
ここまでで気づいた方もいるかと思いますが、\(L_n=\frac{\sqrt{2}}{2}L_{n-1}\)という規則性があります。
すなわち、\(L\)は初項\(1\)、公比\(\frac{\sqrt{2}}{2}\)の等比数列の和になっています。
項数については、「限りなく近づいた」という表現から、無限に近い回数の操作を繰り返すものと考えて、\(n\rightarrow\infty\)とします。
「操作を無限に繰り返したら、針金の長さも無限になっちゃうんじゃないの?」と思われそうですが、「公比が0より大きく1より小さい数であれば、和は一つの値に収束する」という数学界の常識があります。
なんでそうなるかは……数学の世界は奥が深すぎるのであまり深入りしないことをおすすめします。
話を戻すと、本問の場合は公比が\(\frac{\sqrt{2}}{2}\)という、0より大きく1より小さい値なので、\(L\)は一つの値に収束します。
かつ、その値は初項を\(a\)、公比を\(r\)とすると\(\frac{a}{1-r}\)と表せる(これも数学界の決まりです)ので、\(L\)は次のように求められます。
\[
L=\frac{1}{1-\frac{\sqrt{2}}{2}}=2+\sqrt{2}
\]
したがって、2が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
無限等比級数の問題でした。
冒頭にも書いた通り、ある決まった操作を何回も繰り返す、という問題は規則性を問うている場合がほとんどです。
このような問題では、まずは3ステップ目くらいまでの値なり、状況なりを具体化してみることが必要となります。
多くても10ステップ目くらいまでを書き出せば、何らかの規則性には気づけるはずです。
本問では、\(L_n\)が\(L_{n-1}\)の\(\frac{\sqrt{2}}{2}\)倍になっていることから、無限等比級数の問題として処理しました。
無限等比級数は、数的処理なら\(\frac{a}{1-r}\)であることを暗記しておけば十分です。
ちなみに、項数が有限の場合の数列(等差数列、等比数列)の和の公式も重要なので、いつでも使えるようにしておいてくださいね。
国家総合職での出題は多くはありませんが、解答を得るまでの過程で使うことがあるので注意です。
もし数列の和で簡単な問題が出たときに落とさないように、ある程度は準備しておきましょう。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
線分\(\mathrm{A_0}\mathrm{A_1}\)、\(\mathrm{A_1}\mathrm{A_2}\)、\(\mathrm{A_2}\mathrm{A_3}\)、……の長さをそれぞれ\(L_1\)、\(L_2\)、\(L_3\)、……とおき、針金の全長を\(L\)とする。
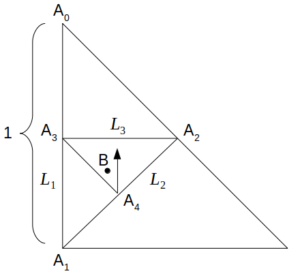
Lnの設定
まず、\(L_1=1\)であるから、\(L=1\)
次に、\(L_2\)について、△\(\mathrm{A_0}\mathrm{A_1}\mathrm{A_2}\)が直角二等辺三角形であることから、\(L_2=\frac{\sqrt{2}}{2}\)
よって、\(L=L_1+L_2=1+\frac{\sqrt{2}}{2}\)
また、\(L_3\)について、△\(\mathrm{A_1}\mathrm{A_2}\mathrm{A_3}\)が直角二等辺三角形であるから、\(L_3=\frac{\sqrt{2}}{2}L_2=\frac{1}{2}\)
よって、\(L=L_1+L_2+L_3=1+\frac{\sqrt{2}}{2}+\frac{1}{2}=\frac{3+\sqrt{2}}{2}\)
さらに、\(L_4\)について、△\(\mathrm{A_2}\mathrm{A_3}\mathrm{A_4}\)が直角二等辺三角形であるから、\(L_4=\frac{\sqrt{2}}{2}L_3=\frac{\sqrt{2}}{4}\)
よって、\(L=L_1+L_2+L_3+L_4=1+\frac{\sqrt{2}}{2}+\frac{1}{2}+\frac{\sqrt{2}}{4}=\frac{6+3\sqrt{2}}{4}\)
ここまでの結果から、\(L_n=\frac{\sqrt{2}}{2}L_{n-1}\)
すなわち、\(L\)は初項\(1\)、公比\(\frac{\sqrt{2}}{2}\)の等比数列の和である。
項数については、「限りなく近づいた」という表現から、\(n\rightarrow\infty\)と考える。
初項を\(a\)、公比を\(r\)とすると\(\frac{a}{1-r}\)と表せるから、\(L\)は次のように求められる。
\[
L=\frac{1}{1-\frac{\sqrt{2}}{2}}=2+\sqrt{2}
\]
よって、正解は2である。

コメント