こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、最短ではない経路の本数を数える問題をやりましたね。
場合の数では定番の、経路数を数える問題です。
基礎的な解法が身に付いているか、力試ししませんか?
もう解いた方も、時間をおいて再度チャレンジすることをおすすめします。
復習のやり方として、解説を眺めるだけの勉強法も悪くないですが、もう一度手を動かして1から解いてみるのがベターです。
実際にやり直してみると、なかなか正答に至らないケースも多いでしょう。
解き直しで手詰まったら成長のチャンスです。
「なぜ手詰まったのか?」を自分なりに分析したら、その原因を解消できるように解説を読み込みましょう。
こうすることで、解法に対する「新しい解釈」が得られ、他の問題に応用が利きやすくなります。
本番で同じ解法を使う問題が出たら、ぜひとも得点したいですよね。
解き直しで知識を定着させ、「解ける問題」を増やしていきましょう!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
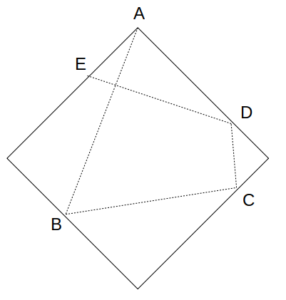
図のように、1辺の長さが1である正方形の一つの頂点Aから発した光が、辺上の点B、C、Dで反射したのち、点Eにおいて観測されたとする。線分AEの長さが\(\frac{5}{7}\)であるとき、点線で示される光路の長さ(線分AB、BC、CD、DEの和)はいくらか。
ただし、各反射点において、辺に対する光線の入射角と反射角は等しいものとする。
- \(\frac{9}{7}\)
- \(\frac{9\sqrt{13}}{7}\)
- \(\frac{\sqrt{457}}{7}\)
- \(\frac{10\sqrt{5}}{7}\)
- \(\frac{\sqrt{636}}{7}\)
3
光の反射の問題です。
(入射角)=(反射角)をどう利用するかがポイント。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
(入射角)=(反射角)
であるならば、正方形の各辺をセンターにした線対称の鏡像を考えれば、光路を「折れ線」ではなく「直線」として捉え直すことができます。
もう少し詳しく言うと、次図のように、対称移動による「反射角のコピー」と入射角が対頂角の関係にあり、これらが等しいので、入射光と「反射光のコピー」は直線となります。
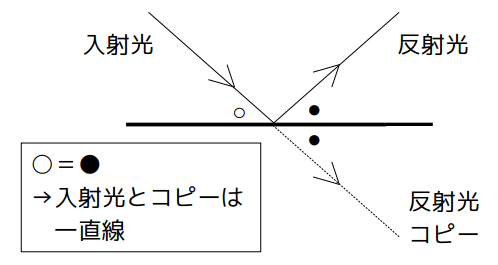
この対称移動を各反射点に対して行うことにより、最終的には点A、B、C、D、Eが一直線上に並びます。
これを利用しましょう。
まず、点Bを含む辺に関する線対称を考えます。
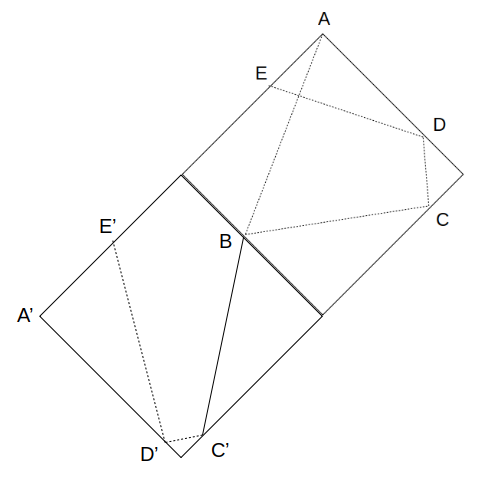
図のように展開すると、線分BCのコピーは線分BC’であり、3点A、B、C’が一直線上に並びます。
次に、点Cを含む辺に関する線対称ですが、こちらは点C’の線分に関して展開すればよいですね。
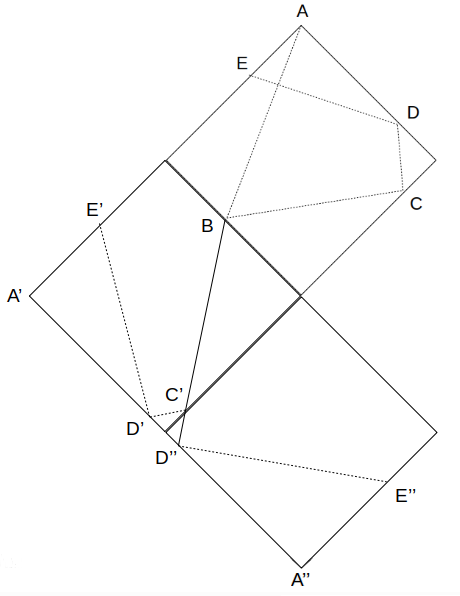
展開すると、線分C’D’(=CD)は線分C’D”へコピーされ、4点A、B、C’、D”が一直線上に並びます。
「問題演習、あと一問やりたいけど、もう疲れて気力がない……」
そんなあなたにおすすめの一問!
解法を知ってさえいれば、あまり迷わずに解けてしまう問題です。
ちょっと考えて分からなければ、解説を見て「ふーん」でOKです。
気軽な感じでチャレンジしてみませんか?
Twitterもよろしくね!↓
あとは点Dの辺に関する線対称ですが、同じように、点D”の線分に関して展開すればOKです。
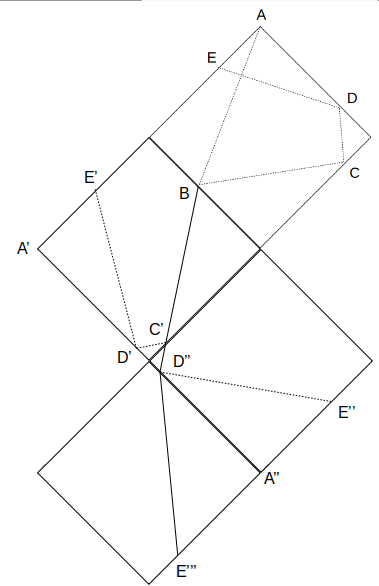
線分D”E”(=DE)は線分D”E”’にコピーされ、5点A、B、C’、D”、E”’が一直線上です。
この直線の長さを求めるには、次図のような直角三角形AHE”’を考えます。
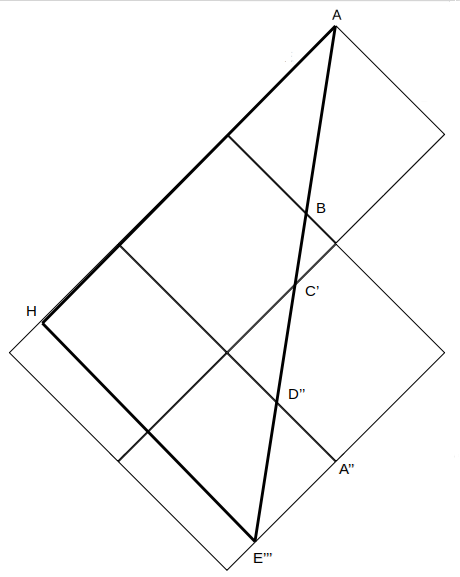
AE=A”E”’=\(\frac{5}{7}\)であったことを思い出すと、AH=\(\frac{19}{7}\)
三平方の定理より、AE”’\(=\sqrt{(\frac{19}{7})^2+2^2}=\frac{\sqrt{457}}{7}\)
よって、3が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
反射の法則を使って、光がたどった経路の長さを求める問題でした。
「線対称で展開して直線にする」という発想を、何もないところから生み出すのは難しいと思います。
なので、解けなかった方もあまり落ち込まなくて大丈夫です。
ただし、本番で同じような問題が出たときのために、こういう解き方もあるんだ、ということは知っておきましょう。
平面図形は数的処理の中でも大きな分野の一つなだけに、狙われやすい分野でもあります。
ありがちなのは面積を問う問題で、主に公式を使うパターンと相似比を使うパターンがあります。
本サイトでも何回か扱っているので、よかったらのぞいてみてください!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
正方形の各辺について線対称に展開していくと、5つの反射点が一直線上に並ぶ。
例えば、点Bを含む辺について線対称に展開すると、次図のように3点A、B、C’が直線となる。
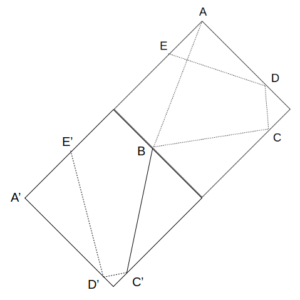
点Bを含む辺に関する線対称
このようにして順次線対称に展開していくと、最終的にAからEに至る光路を一つの直線として捉えることができる。
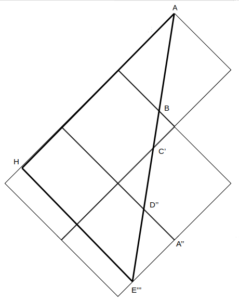
三平方の定理で光路長を求める
あとは、AE=AE”’=\(\frac{5}{7}\)であるから、直角三角形AHE”’に対し三平方の定理を用いることができる。
AE”’\(=\sqrt{(\frac{19}{7})^2+2^2}=\frac{\sqrt{457}}{7}\)
したがって、3が正解である。

コメント