こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
1年で最も長い夜のお供に、数的処理の演習問題はいかが?
前回は、新年度が始まる前後における見取り図の変化を明らかにする問題をやりましたね。
判断推理の重要単元の一つである位置関係の問題なので、まだ解いてない方はぜひ挑戦してみてください。
もう解いた方は、解き直しを忘れずに。
やってみると分かりますが、同じ問題であっても、ただ一度解説を読んだだけで最後まで解ききるって案外難しいものです。
全く同じ問題が解けないのでは、もし同じ「ような」問題が本番で出たとしても、取りこぼしてしまう可能性の方が大きいですよね。
せっかく問題演習しているのに、それではあまりにもったいないです。
経験値を増やして対応できる問題の幅を広げていく、というのが問題演習の狙いなわけですから、見たことある、解いたことある問題くらいは確実に得点したいものです。
そこで必要となるのが「解き直し」です。
解き直しにより、解法を暗記できるのはもちろんですが、本当の狙いは「理解が浅い部分を自分で認識する」ことにあります。
したがって、この時点では自力で正答にたどり着けなくても問題ありません。
途中で手が止まって、理解しきれていなかった箇所が明らかになれば儲けものです。
手が止まったら、今度は解法のその部分を集中的に検討します。
こうすることで、1回目とは異なった角度から解法を理解することができるようになります。
これを繰り返すことで、解法に対する理解が盤石なものになり、少し手が加えられた初見の応用問題にも対応できるようになります。
これが俗に言う「センス」ではないかと私は思っております。
解き直しを取り入れて、初見の問題に正解する快感をぜひ味わってほしいものです。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
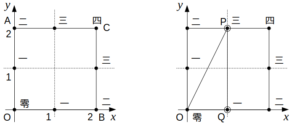
次図(左)のように、\(xy\)平面上に4点O(0, 0)、A(2, 0)、B(0, 2)、C(2, 2)をとり、折れ線OAC上およびOBC上にある格子点に「零〜四」の漢数字を割り当てる。また、折れ線OAC上およびOBC上にある格子点のいずれかに止まる点をそれぞれP、Qとする。
いま、大小2つのサイコロを振り、出た目を5で割った余りに対応する漢数字の格子点にPおよびQをそれぞれ配置することを考える。例えば、大きいサイコロの目が3、小さいサイコロの目が1であった場合のPおよびQは、次図(右)に示す配置となる。このとき、△OPQの面積の期待値として正しいのは次のうちどれか。
- \(\frac{1}{2}\)
- \(\frac{5}{8}\)
- \(\frac{2}{3}\)
- \(\frac{17}{24}\)
- \(\frac{41}{36}\)
4
原点と2つの格子点を頂点とする三角形の面積の期待値を求める問題です。
三角形の形状ごとに場合分けして考える必要がありそうですね。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
移動する点が2つ(PとQ)ある状態のままでは扱いづらいので、1点を固定してしまいましょう。
具体的には、先に点Pの位置を決め打ちした上で点Qを動かし、逐一△OPQの面積を確率とともに求め、合計することで面積の期待値を算出します。
(i)P(0, 0)のとき
大きいサイコロの目が5で、点PがO(0, 0)に一致する場合です。
この場合、点Qがどの位置にあろうと△OPQの面積は0なので、期待値も0です。
(ii)P(0, 1)のとき
大きいサイコロの目が1または6(確率\(\frac{1}{3}\))の場合です。
この場合に、点Qの位置によって個別に期待値を求めると次のようになります。
| 小サイコロの目 | Qの確率 | △OPQ | 期待値 | |
| Q(0, 0) | 5 | \(\frac{1}{6}\) | 0 | 0 |
| Q(1, 0) | 1または6 | \(\frac{1}{3}\) | \(\frac{1}{2}\) | \(\frac{1}{18}\) |
| Q(2, 0) | 2 | \(\frac{1}{6}\) | 1 | \(\frac{1}{18}\) |
| Q(2, 1) | 3 | \(\frac{1}{6}\) | 1 | \(\frac{1}{18}\) |
| Q(2, 2) | 4 | \(\frac{1}{6}\) | 1 | \(\frac{1}{18}\) |
表より、この場合の面積の期待値は、\(0+\frac{1}{18}+\frac{1}{18}+\frac{1}{18}+\frac{1}{18}=\frac{2}{9}\)
(iii)P(0, 2)のとき
大きいサイコロの目が2(確率\(\frac{1}{6}\))の場合です。
| 小サイコロの目 | Qの確率 | △OPQ | 期待値 | |
| Q(0, 0) | 5 | \(\frac{1}{6}\) | 0 | 0 |
| Q(1, 0) | 1または6 | \(\frac{1}{3}\) | 1 | \(\frac{1}{18}\) |
| Q(2, 0) | 2 | \(\frac{1}{6}\) | 2 | \(\frac{1}{18}\) |
| Q(2, 1) | 3 | \(\frac{1}{6}\) | 1 | \(\frac{1}{36}\) |
| Q(2, 2) | 4 | \(\frac{1}{6}\) | 1 | \(\frac{1}{36}\) |
表より、この場合の面積の期待値は、\(0+\frac{1}{18}+\frac{1}{18}+\frac{1}{36}+\frac{1}{36}=\frac{1}{6}\)
(iv)P(1, 2)のとき
大きいサイコロの目が3(確率\(\frac{1}{6}\))の場合です。
| 小サイコロの目 | Qの確率 | △OPQ | 期待値 | |
| Q(0, 0) | 5 | \(\frac{1}{6}\) | 0 | 0 |
| Q(1, 0) | 1または6 | \(\frac{1}{3}\) | 1 | \(\frac{1}{18}\) |
| Q(2, 0) | 2 | \(\frac{1}{6}\) | 2 | \(\frac{1}{18}\) |
| Q(2, 1) | 3 | \(\frac{1}{6}\) | \(\frac{3}{2}\) | \(\frac{1}{24}\) |
| Q(2, 2) | 4 | \(\frac{1}{6}\) | 1 | \(\frac{1}{36}\) |
表より、この場合の面積の期待値は、\(0+\frac{1}{18}+\frac{1}{18}+\frac{1}{24}+\frac{1}{36}=\frac{13}{72}\)
(v)P(2, 2)のとき
大きいサイコロの目が4(確率\(\frac{1}{6}\))の場合です。
| 小サイコロの目 | Qの確率 | △OPQ | 期待値 | |
| Q(0, 0) | 5 | \(\frac{1}{6}\) | 0 | 0 |
| Q(1, 0) | 1または6 | \(\frac{1}{3}\) | 1 | \(\frac{1}{18}\) |
| Q(2, 0) | 2 | \(\frac{1}{6}\) | 2 | \(\frac{1}{18}\) |
| Q(2, 1) | 3 | \(\frac{1}{6}\) | 1 | \(\frac{1}{36}\) |
| Q(2, 2) | 4 | \(\frac{1}{6}\) | 0 | 0 |
表より、この場合の面積の期待値は、\(0+\frac{1}{18}+\frac{1}{18}+\frac{1}{36}+0=\frac{5}{36}\)
以上、(i)〜(v)より、△OPQの面積の期待値は、\(0+\frac{2}{9}+\frac{1}{6}+\frac{13}{72}+\frac{5}{36}=\frac{17}{24}\)
よって、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
格子点を頂点とする三角形の面積の期待値を求める問題でした。
一方を固定して他方を動かす方針を立てたら、あとは地道に計算するだけです。
解説に示したような表を作る発想ができれば、見通しが良くなるでしょう。
計算の過程では分数が入り乱れるので、ミスのないよう慎重に進めましょう。
なお、PおよびQが格子点に止まる確率について、「一」の格子点のみ\(\frac{1}{3}\)(=該当するサイコロの目が2つ)であることに注意です。
原題では全ての格子点が等確率、という設定だったのですが、本問はこの「\(\frac{1}{3}\)」があるためにPとQの確率も個別に考えなければならず、若干の手間が加わっています。
国家総合職の数的処理において、確率は重要かつ頻出の単元であり、決して対策をおろそかにはできません。
出題パターンとしては場合の数を基礎にした問題が多いので、苦手な方は先に場合の数から基盤を固めるのがいいでしょう。
場合の数を攻略できれば、確率の問題にもある程度対応できるようになってくるはずです。
場合の数の基本は「数え上げ」です。
樹形図なども活用しながら、全ての分岐を網羅できるように練習しましょう。
実はこれだけでもある程度は国家総合職の過去問も解くことができます。
確率で何を対策してよいか迷ったら、まずは場合の数、それも単純な数え上げの問題から手を付けることをおすすめします。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
以下、点Pの座標により場合分けする。
(i)P(0, 0)のとき
この場合、点Qの位置によらず△OPQの面積は0なので、期待値も0である。
(ii)P(0, 1)のとき
大きいサイコロの目が1または6(確率\(\frac{1}{3}\))の場合である。
| 小サイコロの目 | Qの確率 | △OPQ | 期待値 | |
| Q(0, 0) | 5 | \(\frac{1}{6}\) | 0 | 0 |
| Q(1, 0) | 1または6 | \(\frac{1}{3}\) | \(\frac{1}{2}\) | \(\frac{1}{18}\) |
| Q(2, 0) | 2 | \(\frac{1}{6}\) | 1 | \(\frac{1}{18}\) |
| Q(2, 1) | 3 | \(\frac{1}{6}\) | 1 | \(\frac{1}{18}\) |
| Q(2, 2) | 4 | \(\frac{1}{6}\) | 1 | \(\frac{1}{18}\) |
表より、この場合の面積の期待値は、\(0+\frac{1}{18}+\frac{1}{18}+\frac{1}{18}+\frac{1}{18}=\frac{2}{9}\)
(iii)P(0, 2)のとき
大きいサイコロの目が2(確率\(\frac{1}{6}\))の場合である。
| 小サイコロの目 | Qの確率 | △OPQ | 期待値 | |
| Q(0, 0) | 5 | \(\frac{1}{6}\) | 0 | 0 |
| Q(1, 0) | 1または6 | \(\frac{1}{3}\) | 1 | \(\frac{1}{18}\) |
| Q(2, 0) | 2 | \(\frac{1}{6}\) | 2 | \(\frac{1}{18}\) |
| Q(2, 1) | 3 | \(\frac{1}{6}\) | 1 | \(\frac{1}{36}\) |
| Q(2, 2) | 4 | \(\frac{1}{6}\) | 1 | \(\frac{1}{36}\) |
表より、この場合の面積の期待値は、\(0+\frac{1}{18}+\frac{1}{18}+\frac{1}{36}+\frac{1}{36}=\frac{1}{6}\)
(iv)P(1, 2)のとき
大きいサイコロの目が3(確率\(\frac{1}{6}\))の場合である。
| 小サイコロの目 | Qの確率 | △OPQ | 期待値 | |
| Q(0, 0) | 5 | \(\frac{1}{6}\) | 0 | 0 |
| Q(1, 0) | 1または6 | \(\frac{1}{3}\) | 1 | \(\frac{1}{18}\) |
| Q(2, 0) | 2 | \(\frac{1}{6}\) | 2 | \(\frac{1}{18}\) |
| Q(2, 1) | 3 | \(\frac{1}{6}\) | \(\frac{3}{2}\) | \(\frac{1}{24}\) |
| Q(2, 2) | 4 | \(\frac{1}{6}\) | 1 | \(\frac{1}{36}\) |
表より、この場合の面積の期待値は、\(0+\frac{1}{18}+\frac{1}{18}+\frac{1}{24}+\frac{1}{36}=\frac{13}{72}\)
(v)P(2, 2)のとき
大きいサイコロの目が4(確率\(\frac{1}{6}\))の場合である。
| 小サイコロの目 | Qの確率 | △OPQ | 期待値 | |
| Q(0, 0) | 5 | \(\frac{1}{6}\) | 0 | 0 |
| Q(1, 0) | 1または6 | \(\frac{1}{3}\) | 1 | \(\frac{1}{18}\) |
| Q(2, 0) | 2 | \(\frac{1}{6}\) | 2 | \(\frac{1}{18}\) |
| Q(2, 1) | 3 | \(\frac{1}{6}\) | 1 | \(\frac{1}{36}\) |
| Q(2, 2) | 4 | \(\frac{1}{6}\) | 0 | 0 |
表より、この場合の面積の期待値は、\(0+\frac{1}{18}+\frac{1}{18}+\frac{1}{36}+0=\frac{5}{36}\)
以上、(i)〜(v)より、△OPQの面積の期待値は、\(0+\frac{2}{9}+\frac{1}{6}+\frac{13}{72}+\frac{5}{36}=\frac{17}{24}\)
よって、正解は4である。

コメント