こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
今一番欲しいもの:机とイス
引っ越したばかりで物がなさすぎる。
前回は、購入した果物の総数を求める問題をやりましたね。
国家総合職で頻出の、整数問題に対応する力が身につく記事なので、解いてない方はぜひ挑戦してみてください。
もう解いた方は、どんな流れで解いたか、もう一度思い出してみましょう。
こう言われて思い出すことは、解法の中でも要点である可能性が高いところなので重要です。
忘れずに身に付けましょう。
あとは、皆さんが悩んだりつまづいたところも忘れてはならないポイントです。
(これは私の解説が分かりにくかった可能性もありますね……がんばりましょう)
できなかった思い出を貯金するのは少々つらいかもしれませんが、本番で得点できれば勝ちです。
もし、思い出せない箇所があれば、戻って記事を読み返すのもおすすめです。
解いた問題を確実に蓄積していけば、試験は必ずパスできるので、根気よくいきましょう!
復習がバッチリな方は、本日の問題へ参りましょう。
本日の演習問題
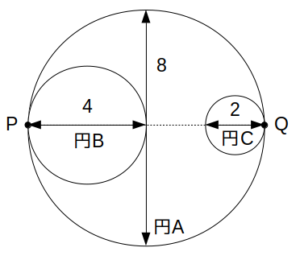
図のように、直径が8の円の内部に、直径が4の円Bと直径2の円Cが、それぞれ点PとQを接点として内接している。いま、PとQ、および3つの円の中心が一直線上に並ぶ状態からスタートして、円Bと円Cが円Aの内側を滑ることなく回転し、1周して元の位置に戻ってくるとする。このとき、円Bの円周上に固定された点Pと、円Cの円周上に固定された点Qが描く軌跡として正しいのは次のうちどれか。

2
内接円が滑らずに転がる軌跡の問題です。
点Pと点Qが描く軌跡をそれぞれ個別に求めましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
(本問では、点や円の位置を時計の針が指す位置にたとえて説明します。)
まず、円B上の点Pが描く軌跡から考えてみます。
円Bが滑らずに転がるとき、円Bの中心と点Pとの相対的な位置関係(=円Bの中心から見た点Pの位置)の変化量は、中心の移動量に等しくなります。
例えば、円Bの中心が\(\pi\)だけ動いたら、中心から見た点Pの位置も\(\pi\)だけ移動することになり、中心から見て9時の位置にあったPは12時の位置に移動することになります。
このことと、円Bの中心が半径2の円を描くことを踏まえ、円Bが9時→6時→3時→12時→9時と1周するときの点Pの相対的な位置の変化を追うことで、点Pの軌跡をたどります。
まず、円Bが9時→6時と移動すると、中心は\(4\pi×\frac{1}{4}=\pi\)だけ移動します。
円Bの円周は\(4\pi\)なので、中心から見た点Pの位置は9時→12時と移ります。(P0→P1)
今度は円Bが6時→3時と移動するとき、中心の移動量は同じく\(\pi\)なので、中心から見た点Pの位置は12時→3時と移動します。(P1→P2)
同様に、円Bが3時→12時と移動するとき、中心から見た点Pの位置は3時→6時と移動します。(P2→P3)
円Bが12時→9時と移動するとき、中心から見た点Pの位置は6時→9時と移動します。(P3→P4)
以上を図示すると、点Pの動きは次のようになります。
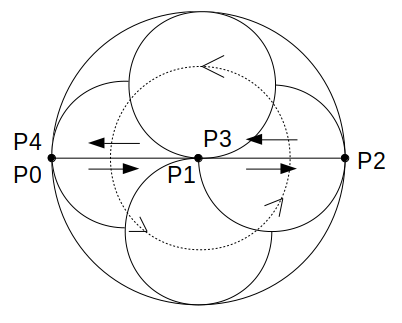
P0〜P4間の点Pの動きを脳内で補完すると、点Pの軌跡は図のような水平線となりますね。
同じように、円Cが3時→12時→9時→6時→3時と1周するときの点Qの相対的な位置の変化を追うことで、点Qの軌跡を求めます。
まず、円Cが滑ることなく転がって1周するとき、中心は半径3の円を描くことを押さえましょう。
円Cが3時→12時と移動すると、中心は\(6\pi×\frac{1}{4}=\frac{3}{2}\pi\)だけ移動します。
円Cの円周は\(2\pi\)なので、中心に対する点Qの位置は時計回りに\(frac{3}{4}\)回転して3時→12時と変化します。(Q0→Q1)
ここから円Cが12時→9時と移動すると、中心に対して点Qは同じく時計回りに\(frac{3}{4}\)回転して12時→9時と変化します。(Q1→Q2)
同様に、円Cが9時→6時と移動すると、中心に対して点Qは時計回りに\(frac{3}{4}\)回転して9時→6時と移ります。(Q2→Q3)
円Cが6時→3時と移動するときは、中心に対する点Qの位置は時計回りに\(frac{3}{4}\)回転して6時→3時と移ります。(Q3→Q4)
以上を図示すると次のようになります。
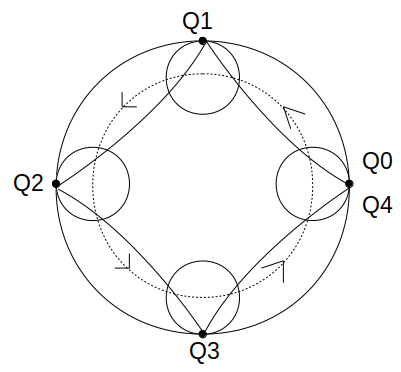
Q0→Q4間における点Qの動きを脳内で補完すると、この図のような経路を描きます。
脳内補完が難しければ、Q0〜Q4が全て円Aとの接点となること(=点Qが4回接点となること)より、選択肢から考えて図のような曲線になるしかない、と考えてもOKです。
以上より、2が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
このサイトで扱うのは何気に初めてな、軌跡の問題でした。
軌跡を求める問題は、国家総合職では頻出の部類に入ると思います。
本問のような軌道の形そのものを問う問題のほか、軌道の長さを求める問題も出題されています。
どちらのパターンでも、分かりやすいようにキリのいいところで分割して考えるのがコツです。
例えば本問では、時計の3時、6時、9時、12時の4箇所に来るときの点の位置を考えて、間を脳内で補完する、という手順でしたね。
特に点Qの軌跡では、円Cが3時、6時、9時、12時の4点に来るときは、ちょうど点Qが接点になる特徴的なタイミングなので、軌跡の形状を知るのには好都合だったのです。
あとは解説の最後にも書いてますが、脳内補完が難しい場合は軌跡の形の特徴だけ把握して、あとは選択肢からその特徴を満たす図形を選ぶ、というアプローチもアリです。
選択肢から逆算的に解答を導き出す方法が有効であることは、本サイトでも何度か書いてますね。
正攻法で解くのが難しければ、選択肢から逆算できないか、という方向も検討してみてください。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
円Bが円Aの内部を滑ることなく転がるとき、円Bの中心は半径2(円周\(4\pi\))の円を描く。
このとき、円Bの中心から見た点Pの位置の移動量も\(4\pi\)となる。
以下、円Bの位置が9時→6時→3時→12時→9時と1周するときの点Pの位置の変化を追うことで、点Pの軌跡を求める。
まず、円Bが9時→6時と移動すると、中心は\(4\pi×\frac{1}{4}=\pi\)だけ移動する。
円Bの円周は\(4\pi\)であるから、中心から見た点Pの位置は時計回りに\(\frac{1}{4}\)だけ回って9時→12時と移る。(P0→P1)
円Bが6時→3時と移動するとき、中心の移動量は同じく\(\pi\)であり、中心から見た点Pの位置は時計回りに\(\frac{1}{4}\)だけ回って12時→3時と移動する。(P1→P2)
円Bが3時→12時と移動するとき、中心から見た点Pの位置は3時→6時と移動する。(P2→P3)
円Bが12時→9時と移動するとき、中心から見た点Pの位置は6時→9時と移動する。(P3→P4)
以上を図示すると次のようになる。
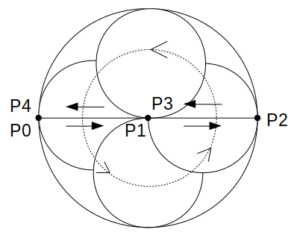
点Pの軌跡
P0〜P4の中間の動きを含めると、点Pの軌跡は図のような水平線となる。
次に、円Cが3時→12時→9時→6時→3時と1周するときの点Qの位置の変化を追うことで、点Qの軌跡を求める。
円Cが滑ることなく転がって1周するとき、中心は半径3(円周\(6\pi\))の円を描く。
円Cが3時→12時と移動すると、中心は\(6\pi×\frac{1}{4}=\frac{3}{2}\pi\)だけ移動する。
円Cの円周は\(2\pi\)であるから、中心に対する点Qの位置は時計回りに\(frac{3}{4}\)回転して3時→12時と変化する。(Q0→Q1)
円Cが12時→9時と移動すると、中心に対して点Qは同じく時計回りに\(frac{3}{4}\)回転して12時→9時と変化する。(Q1→Q2)
円Cが9時→6時と移動すると、中心に対して点Qは時計回りに\(frac{3}{4}\)回転して9時→6時と移動する。(Q2→Q3)
円Cが6時→3時と移動すると、中心に対する点Qの位置は時計回りに\(frac{3}{4}\)回転して6時→3時と移動する。(Q3→Q4)
以上を図示すると次のようになる。
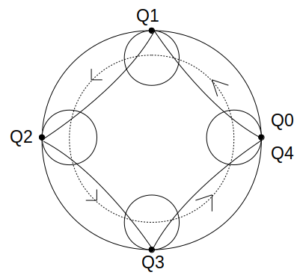
点Qの軌跡
Q0〜Q4の中間の動きを含めると、点Qの軌跡は図のような曲線となる。
以上から、正解は2である。

コメント