こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます！
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
ひっそりとTwitter始めました↓
Follow @Xk2cZraSP34NygP
前回は、トーナメントの決勝戦に勝ち残る確率を求める問題をやりましたね。
数的処理では定番、確率分野に対する基本的なアプローチが学べる問題です。
まだ問題を見てない方はぜひ挑戦してみてください。
今回のテーマは「場合の数」です。
場合の数（と確率）を解くための道具は５つあり、ほとんどの問題はそれらの合わせ技で解けます。
「５つの道具」が何なのか知りたい方は、以下の記事をクリック！
演習問題：最短ではない経路の数え方
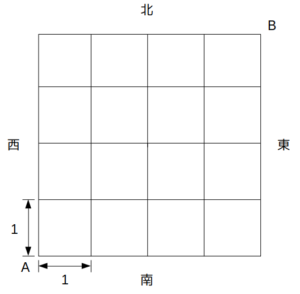
図のように、1辺の長さが1である正方形からなる経路図において、地点Aから地点Bへ至る方法を考える。同じ正方形の辺上を何度も行き来できるものとすると、地点Aから地点Bへ至る経路のうち、長さが10であるものは何通りあるか。
ただし、図に示した経路以外の道を通ることはないものとする。また、移動の過程で地点Bを複数回訪れることはあり得るものとする。
- 960通り
- 1240通り
- 1450通り
- 1680通り
- 1870通り
４
決められた地点間を結ぶ経路の数をかぞえる問題です。
ほしいのは「長さが10」の経路数ですが、それがどんな経路なのか？をまず考えましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート！
図のように、1辺の長さが1である正方形からなる経路図において、地点Aから地点Bへ至る方法を考える。同じ正方形の辺上を何度も行き来できるものとすると、地点Aから地点Bへ至る経路のうち、長さが10であるものは何通りあるか。
ただし、図に示した経路以外の道を通ることはないものとする。また、移動の過程で地点Bを複数回訪れることはあり得るものとする。
- 960通り
- 1240通り
- 1450通り
- 1680通り
- 1870通り
解説
そもそも、「長さが10」の経路とは何でしょう？
この手の問題では最短経路が取り上げられがちですが、本問は違います。
与えられた図によると、AからBへ至る最短経路の長さは「8」だからです。
ここに長さが2だけ加わった経路とは、最短ルートを進むうちのどこかのタイミングで、1回だけ南向きまたは西向きの格子点に移動した場合の経路に他なりません。
最短経路に、「行って戻る」という移動が一つ加わわれば１０になる
まずは最短経路を数え出します。
そこに1回だけ南向きまたは西向きの移動を加えたルートはいくつあるか？を数えればOKです。
最短経路の数え方としては、メジャーなのは「↑↑→↑→→↑→」のような矢印の並び方を順列の考え方を使って数える方法ですが、今回は違う方法で解きます。
順列の考え方も使うけどね
どんな方法かというと、「図に数字を書き込んで直接数え上げる方法」です。
こっちもよく知られた方法で、普通の参考書には載っているようなものです。
そんなの知らない、という方は、ぜひここで習得していってください。
念のため、図を使って経路をカウントする方法の基本的な考え方を以下で説明します。
もう分かってるって方は読み飛ばしてOK。
この数え方は、本サイトの「解法のポイント」にいう、２と３を組み合わせた方法になります。
直前の地点に至る最短経路（排反）を、↑と→の順列で数えて足し合わせる
-
事象をカウントし定義から求めるやり方
- 樹形図や書き出しによる数え上げ
- 組み合わせや順列を使った計算
-
確率から確率を求めるやり方
- 排反事象の足し算（和の法則）
- 独立事象のかけ算（積の法則）
- 全体から引く（余事象の確率）
この考え方を使って、上図から題意の経路数を求めます。
「各格子点へ戻って」Bへ至る経路の数をカウント
例として、経路図で一番右上の、点Bを含む正方形1ブロックに注目します。
このブロックにおいて、「1回戻る」移動を含んだ上で点cを経由し、地点Bへ至るルートがいくつあるのか考えてみましょう。
「1回戻る」移動の結果として点cに止まるパターンは、最短ルートで点bへ至ったのち南向きに1回移動する35通りと、最短ルートで点cへ至ったのち西向きに1回移動する35通りがあります。
合わせて70通りですね。
図を使ってカウントする方法と理屈は同じ
そこ（＝点a）から地点Bへ至る経路数はというと、赤い矢印に示すように、a→b→Bというルートとa→c→Bルートの2通りがあるので、70×2=140通りです。
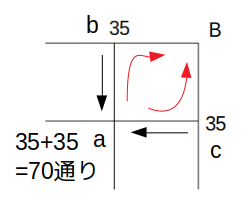
ここで、赤い矢印の2ルートは、点aから地点Bへ至る最短経路に他なりません。
この考え方によると、点a以外の格子点について、「1回戻る」移動を含む経路数も同じロジックで求められます。
定式化すると、次のようになります。
（経路数）＝（A→bの最短経路数＋A→cの最短経路数）×（a→Bの最短経路数）
戻り移動でaへ行き、「かつ」最短でBへ至る（＝積事象）経路だからかけ算ね
a→Bの最短経路数を求めるときには、先述した「矢印の順列」の方法を使うと早いです。
（最初の図で示した「最短経路数」とは異なることに注意）
上式を用いて、長さが10の経路数を格子点ごとに求めると、次図のようになります。
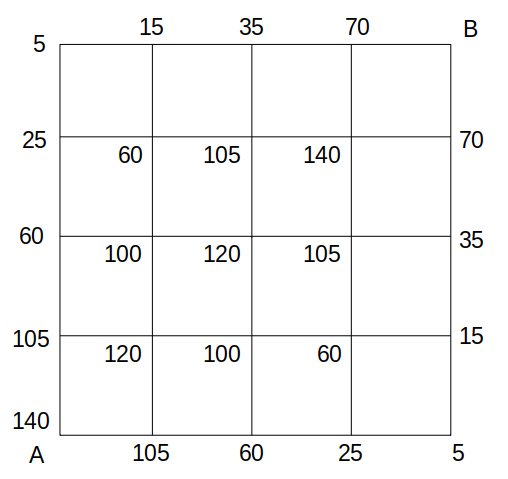
各格子点を通る経路（排反）を足し合わせる
求める経路数は、各点を通る経路数を全て足し合わせたものです。
「ある点に戻ってBへ至る」事象は同時に起こらない（＝排反）から足し算
対角線に関する対称性を利用すると、計算が少し楽になります。
\(140+120+120+140+ \\
(105+60+25+5+100+60+15+105+35+70)×2=1680\)
計算ミスに注意
よって、４が正解です。
おわりに：最短経路は順列もいいけど数え上げもアリ
お疲れ様でした！
いかがだったでしょうか？
最短経路は、矢印の順列で求めるのが基本です。
ですが、本問のように、図に書き込んで数える方法が有効な場合もあります。
前半で最短経路の数を「図に書き込む方式」で数えたら、後半では中継点からの最短経路を数えるのに「矢印の順列」を活用します。
これらはともに常套的な解法なので、両方とも習得しておいて臨機応変に使い分けるのが望ましいです。
片方しか知らない状況だと、本問は厳しいです。
場合の数は数的処理の一角を担う分野で、国家総合職でも高頻度で出題されています。
毎年1問は出ると思っておいていいでしょう。
今回紹介した最短経路問題の解き方は、普通の参考書で学習できる解法なので、ぜひ使いこなしてください。
最後までお読みいただきありがとうございました！
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします！次回もお楽しみに！
次回もお楽しみに！
略解
長さが10である経路とは、最短経路のうちのどこかのタイミングで「1回戻る」（南向きまたは西向きに移動する）経路である。
まず、A→Bの最短経路数を数えると、次図のようになる。
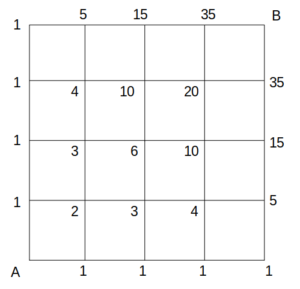
各格子点へ至る経路の数
これをもとに、「1回戻る」移動を含む経路の数を明らかにする。
一番右上の正方形1ブロックを例に、次図の点aを経由し地点Bへ至る経路が何通りあるか考える。
「1回戻って」Bへ至る経路
「1回戻る」移動の結果として点aに止まる経路は、点bからの35通りと、点cからの35通りを合わせて70通りある。
a→Bの経路は、図の赤い矢印で示すように、a→b→Bというルートとa→c→Bというルートで計2通りなので、点aを経由してBへ至る経路の数は、70×2＝140通り
同様の方法で、図の各格子点を経由しBへ至る経路の数を数えると、次図のようになる。
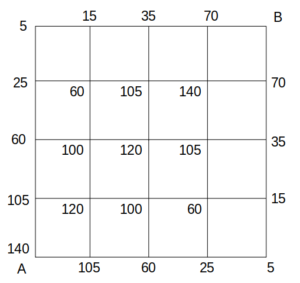
長さが10である経路数
求める経路数は、図の経路数の合計として求められ、
\(140+120+120+140+(105+60+25+5+100+60+15+105+35+70)×2=1680\)（通り）
したがって、４が正解である。
コメント
（選択肢にあれば）1540通りが正解ではないでしょうか
似たような解き方はしたのですが、一度ゴールに入ってからわざわざ戻ってまたゴールに行く140通りは経路と呼べないと思い、除外しました…
スタートに戻るのは経路として受け入れられるのにゴール側が許せないのは、対称性が破れていて面白い気もします(大袈裟
コメントありがとうございます。
おっしゃること、なるほど一理あるなと思いました。
しかし、本問では「一度Bに入ってまた戻る」経路も題意に沿ったルートとして計上できると私は考えます。
本問において、Bは「ゴール」というよりは、あくまでも数ある格子点の一つ、という位置付けなのです。
この考え方でいくと、Aと同じくBも出入りが可能、としなければ、おっしゃる通り対称性も崩れてしまいます。
Bを「ゴール」として解釈するなら、その旨の文言が必要になるところかと思います。
とはいえ、同じような誤解をされる方が他にいるかもしれないので、問題文にただし書きという形で追記しました。
不明な点などあれば、またコメントください。