こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本ブログ、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、正方形を折り返してできる直角三角形の面積を求める問題でしたね。
第6回目になりました。今回も、まずは問題文のチェックから始めましょう!
本日の演習問題
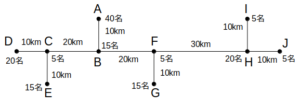
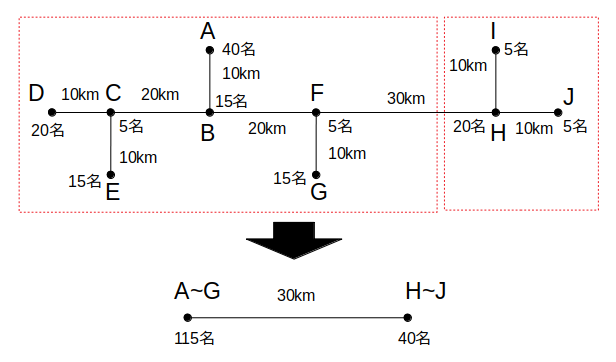
ある商社Pでは、半年に1回、周辺10地域の支社A〜Jに勤務する管理職者を1つの支社に集め、全体ミーティングを行うこととしている。経費削減のため、Pは次回の全体ミーティングの会場として、管理職者の移動にかかる費用が最小となるような支社を選びたいと考えている。支社A〜Jの位置関係と、各社に所属する管理職者の人数は次図の通りである。
このとき、全体ミーティングの会場として適切なのは次のうちどれか。ただし、管理職者の移動にかかる費用は移動距離と人数に比例するものとする。また、管理職者は図に示した経路以外は使用しないものとする。
- A社
- B社
- C社
- F社
- H社
2
経費を最小化する問題ですね。移動距離と人数をもとに、必要な経費を数値で求めて比較する、というのが現実的な解決策となるでしょう。
以下、この問題の詳しい解説ですが、回りくどいのが苦手な方は一番下の略解だけ見る、でも大丈夫です。
それではスタート!
詳しい解説
「ただし、〜」という部分が、この問題を解く足がかりになります。
わざわざ但し書きするくらいですから、重要な情報を含んでいるのだと気づきましょう。
ここに「管理職者の移動にかかる費用は移動距離と人数に比例する」とあるので、経費は具体的に以下の式で求められます。
\[
(経費)=(移動距離)×(人数)×(比例定数a)
\]
本問では「経費がいくらか?」を聞かれているわけではないので、上式の(比例定数\(a\))は省略して、ざっくりと(移動距離)と(人数)だけで決まると見てよいでしょう。
\[
(経費)=(移動距離)×(人数)
\]
この式を用いて、A社、B社、C社、F社、H社が会場となった場合の経費を算出します。
(10社全てについて調べる必要はありません。選択肢はA社、B社、C社、F社、H社の5択なので、これら5つの場合だけ調べれば十分です。「選択肢から逆算する」という考え方はぜひ身に付けておいてください。)
まず、A社が会場となった場合、B〜J社の管理職者の移動にかかる経費をそれぞれ求めます。
例えばB社なら、15人の管理職者が10kmの経路を移動するのですから、経費は\(15×10=150\)となります。
残りのC〜J社についても同様に求めると、
\begin{multline}
\mathrm{C}: 5×30=150 \mathrm{D}:20×40=800 \mathrm{E}:15×40=600 \mathrm{F}:5×30=150 \\
\mathrm{G}:15×40=600 \mathrm{H}:20×60=1200 \mathrm{I}:5×70=350 \mathrm{J}:5×70=350
\end{multline}
なので、合計は
\[
150+150+800+600+150+600+1200+350+350=4350
\]
次に、B社が会場となった場合の経費を求めます。
A社の場合と全く同じやり方でもできますが、ここでは別な解き方を紹介しましょう。
A社が会場だった場合と比較すると、B社の場合は「A社の40人のA→Bの移動」が加わり、そこから「B〜J社の105人のB→Aの移動」がなくなります。
つまり、Aの場合の経費に「40人の10km移動分」を加算し、かつ「105人の10km移動分」を減算したものがBの場合の経費となります。
\[
4350+40×10-105×10=3700
\]
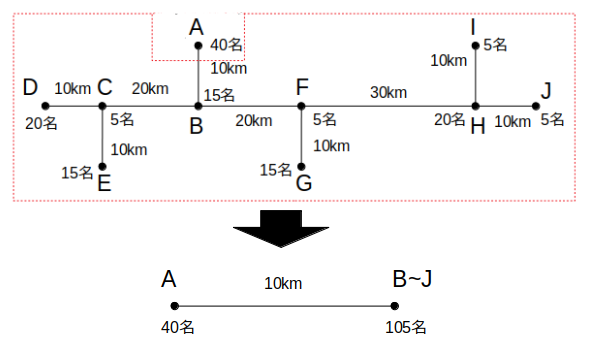
Aが会場である場合よりもBが会場である場合の方が、経費は安く済むのだと分かりましたね。
今度はC社が会場となった場合を考えます。
やり方は同じで、B社の場合に新たに発生する移動分を加え、不要となる移動分を引き算します。
C社の場合は、C社よりも右側にある7社(A、BおよびF〜J)の105人がBC間を移動します。
逆に、C〜Eの3社の40人はBC間の移動がなくなるので、Cが会場であった場合の経費は
\[
3700+105×20-40×20=5000
\]
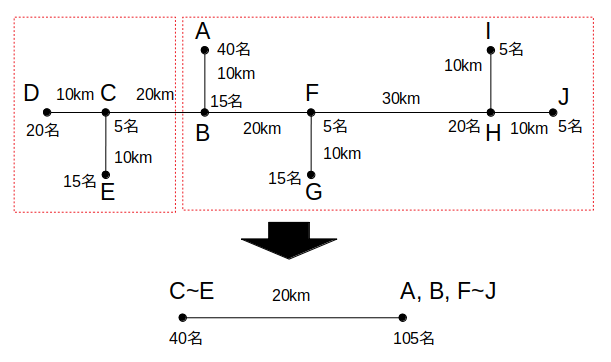
よって、B社が会場となった場合の方がC社よりも安く済みます。
F社が会場だった場合も、B社の場合を手がかりとして求めます。
F社の場合は、F社よりも左側にあるA〜Eの5社の95人がBF間を移動し、F〜Jの5社の50人によるBF間の移動が不要となります。
\[
3700+95×20-50×20=4600
\]
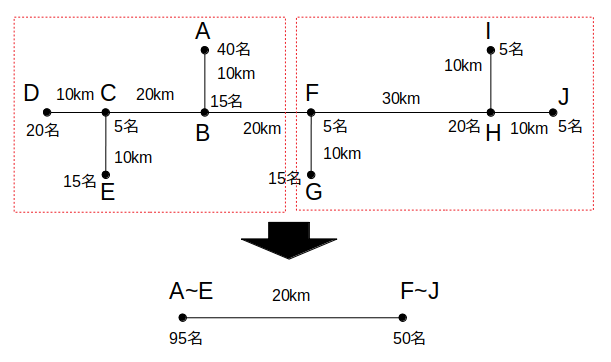
やはりB社の方が安いですね。
H社が会場であった場合の経費は、F社の場合の経費をもとに算出します。
H社よりも左側にあるA〜Gの7社の115人がFH間を移動し、H〜Jの3社の40人によるFH間の移動がなくなるので、この場合の経費は
\[
4600+115×30-40×30=6850
\]
この場合もB社が安いと分かります。
以上から、最終的に経費が最も安いのはB社を会場とした場合で、正解は2となります。
おわりに
お疲れ様でした!
いかがだったでしょうか?
決まった条件が明示されているわけでもなく、どこから手を付けて良いか発想しづらい問題でしたね。
しかし、与えられた情報の中にヒントは必ずあります。
解説では「選択肢から逆算する」という発想を身に付けてほしい、と述べました。
本問は問題文には10社登場してますが、正解は5択のうちのいずれかなので、全ての選択肢の場合を検証してもそれほど手間はかかりません。
上手なやり方を模索するより、しらみ潰しした方が早く正解にたどり着く場合も大いにあります。
数的処理は選択式で解く過程までは考慮されませんから、正解を見つけたもの勝ちです。
全て調べ上げることが可能な問題に関してはしらみ潰しして、他の問題に使える時間を少しでも増やし、得点をアップしましょう!
本ブログでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
これを用いて、まずはA社が会場となった場合の経費を求める。
B〜Jの管理職者の移動にかかる経費をそれぞれ求めると、
\[
\mathrm{B}: 15×10=150 \mathrm{C}: 5×30=150 \mathrm{D}:20×40=800 \\
\mathrm{E}:15×40=600 \mathrm{F}:5×30=150 \mathrm{G}:15×40=600 \\
\mathrm{H}:20×60=1200 \mathrm{I}:5×70=350 \mathrm{J}:5×70=350
\]
合計は、
\[
150+150+800+600+150+600+1200+350+350=4350
\]
これをもとに、B社が会場となった場合の経費を求める。
会場がA社からB社へ移ると、A社の40人がB社へ移動する費用が加算されると同時に、B〜J社の105人がAB間を移動する必要がなくなるので、この分の費用が減算される。
よって、B社が会場であった場合の経費は、
\[
4350+40×10-105×10=3700
\]

「A」と「B〜J」に分けて考える
C社が会場であった場合も、同様にB社の場合をもとに算出する。
会場がB社からC社へ移ると、図でC社よりも右側にある7社(A、BおよびF〜J)の105人によるBC間の移動が生じるとともに、C〜Eの3社の40人によるBC間の移動がなくなるので、経費は
\[
3700+105×20-40×20=5000
\]

「C〜E」と「A、B、F〜J」に分けて考える
F社が会場であった場合も、同じくB社の場合の経費から算出する。
F社よりも左側にあるA〜Eの5社の95人によるBF間の移動が生じ、代わりにF〜Jの5社の50人によるBF間の移動がなくなるので、経費は
\[
3700+95×20-50×20=4600
\]

「A〜E」と「F〜J」に分けて考える
H社が会場であった場合は、F社の場合の経費に基づく以外は同様の手順である。
すなわち、H社よりも左側にあるA〜Gの7社の115人によるFH間の移動が加わり、H〜Jの3社の40人によるFH間の移動がなくなるので、経費は
\[
4600+115×30-40×30=6850
\]

「A〜G」と「H〜J」に分けて考える
以上から、経費が最小となるのはB社を会場とした場合である。
よって、正解は2である。

コメント