こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
国家総合職の過去問解説が一通り終わったら、他の職種の過去問の解説か、参考書にあるような易しい問題の解説とかやってみたいなぁ。
その前に心が折れないように更新を続けたい。
前回は、上皿天秤を使って5つの球の重さを量る問題でした。
判断推理にありがちな、与えられた条件から分かることを推理するタイプの問題です。
定番の解法の流れをつかむのに良い教材となってます。
ぜひ解いてみてください。
もう解いた方は、お疲れ様でした。
しっかり復習して、本番に役立ててください。
復習のやり方として、解法の「研究」ができると理想的です。
解説の内容そのものは目の前の問題にしか通用しないので、個々の解説から他の問題に使える知識をいかに学べるかが重要です。
本サイトでは「解法のポイント」として紹介しているものですが、これをご自身でも探してみてください。
もちろん、「解法のポイント」を頭に入れていただくだけでも効果はあるので、ぜひご活用ください!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
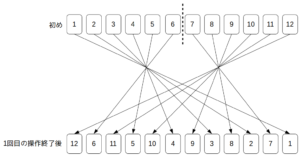
1〜12の数字が一つずつ書かれた12枚のカードを、左から一列かつ昇順に並べた「初め」の状態から始め、次に示す操作を複数回行う。
操作:カードの列を左右6枚ずつの組に分け、「右半分の6枚目→左半分の6枚目→右半分の5枚目→左半分の5枚目→……」という順序で1枚ずつ左から並べる。
上述の「操作」を100回繰り返すとき、1のカードと11のカードが隣り合う回数は何回か。
- 10回
- 12回
- 15回
- 18回
- 20回
1
カードの並べ替え操作を多数回繰り返す問題です。
実際に手を動かして調べるのに、「100回」という回数が現実的でないことは明らかです。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
「100回」という回数を、実際に手を動かして調べるのは現実的に不可能でしょう。
この手の、同じ操作を多数回繰り返す系の問題は、何回か実行してみて規則性を見出すのがセオリー。
私の経験則では、5〜10回くらい繰り返せば何らかの規則性が見えてきます。
本問でも、まずは「操作」を5回繰り返してみましょう。

5回目までの結果のうちに、2つの規則性が表れているのに気づいたでしょうか?
1つは、「1」と「12」のカードの位置です。
この2枚は、必ず両端にあり、かつ1回操作が行われる度に位置が入れ替わっています。
もう1つは、中間の2〜11番目のカードの並びです。
図の通り、この10枚は操作を5回行う度に並びがもとに戻ります。
これらをもとに、6〜10回目の操作の結果を予測できます。
すなわち、6〜10回目の並びは、1〜5回目における「1」と「12」の位置をそれぞれ逆転させたものとなります。
そして、10回の操作でカードの並びがもとに戻り、以降は再び同じ並びが順に現れることになります。
問題は「1のカードと11のカードが隣り合う回数が何回か」ですが、10回の操作のうちで1のカードと11のカードが隣り合うのは5回目のみなので、100回の操作の中では10回あることになります。
よって、1が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
規則性をもとに、カードを並び替える操作の結果を推測する問題でした。
試行回数が極端に多い場合は、何かしらの法則を見抜くことを要求されている場合が多いです。
今回のような力技的な調べ方が通用しないケースは、規則性に基づいて結果を予測する方向に考えましょう。
5回繰り返すうちに両端とそれ以外のカードの並びの規則に気づいて、6〜10回目の結果を推測できるのが理想的ではありますが、今回のケースでは10回目まで手を動かして調べたとしてもそんなに時間はかからないでしょう。
本番は手書きすることになりますが、焦って並び替え操作をミスしないようにくれぐれも注意です。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
「操作」を5回繰り返した結果を次図に示す。

操作を5回繰り返して規則性を見出す
この図から、カードの並びについて次の2つの規則性を見出すことができる。
1つは、「1」と「12」のカードの位置が必ず両端にあり、かつ1回操作が行われる度に位置が入れ替わる、ということである。
もう1つは、2〜11番目のカードの並びが操作を5回行う度にもとに戻る、ということである。
これらをもとに、6〜10回目の操作の結果を予測できる。
6〜10回目の並びは、1〜5回目における「1」と「12」の位置をそれぞれ逆転させたものに他ならない。
10回ごとにカードの並びは「初め」に戻り、11回目以降は1〜10回目の並びが繰り返し現れることになる。
1〜10回目の間に「1」と「11」が隣り合うのは5回目だけなので、操作を100回繰り返した場合に隣り合う回数は合計で10回となる。
したがって、1が正解である。

コメント