こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
今日、家に帰って改めて自分の部屋を眺めてみたんです。
「散らかってるなー」と思いました(思っただけ)。
前回は、6人の発言に基づいて身長の高低を明らかにする問題をやりましたね。
国家総合職の試験に即した形式ではありますが、数的処理の基本的な解法を学べる内容になっているので、解いてない方はぜひ挑戦してみてください。
もう解いた方も、少ししたら解き直しに戻ってみることをおすすめします。
一度解説を読んで納得したつもりでも、いざ自力で解くとなると手詰まってしまうことはよくあります。
この状態では、運良く初見で似たような問題に出会っても取りこぼしてしまうことになります。
これでは、何のために問題演習をしているか分かりませんね。
せめて知っている問題と似た問題くらいは確実に得点したいものです。
一つの解法を深く理解するには、解法のロジックをあらゆる角度から検証してみることが必要になります。
解き直しをすることで、どの視点からの検証が足りていないのかを明確にすることができます。
手詰まったところがそれです。
手詰まったからには、自分の中に何かしら腑に落ちない点があったことと思いますので、今度はそれを解消するように解説を読み返してみてください。
こうすることで、一つの解法に対する理解が深まり、初見の問題に応用できるようになります。
これこそが試験をパスするのに必要な「対応力」なのです。
新しい問題は自力で正答を導けるようになるまで解き直し、自分の道具にしてしまいましょう。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
図のように、1辺が100mの正方形の形をした歩道ABCDがあり、ABとCDの中点を通るように直線状の車道が横切っている。歩道と車道が交わる点にはそれぞれ信号機が設置されており、30秒ごとに赤と青の点灯が切り替わっている。
いま、この歩道上を、甲と乙の2名が一定の速さで周回する。甲はAを出発して反時計回りに18km/hで、乙はDを出発して時計回りに3.6km/hでそれぞれ周回する。信号機が青に点灯した瞬間に2名が同時にスタートしたとき、2回目に甲と乙が出会うまでの時間に最も近いものは次のうちどれか。
ただし、車道を通過するときに信号機が赤の場合は青に変わるまで待つものとする。また、車道を通過する時間は考えないものとする。
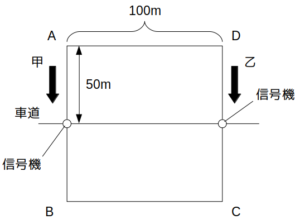
- 2分20秒
- 2分25秒
- 2分30秒
- 2分35秒
- 2分40秒
2
2名が逆方向に進み出し、一定の速さで周回する問題です。
信号機の点灯に注意しつつ、2人の移動を追跡して把握しましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
まず、歩道の長さがメートルで与えられているのに対し、甲乙の速さはキロメートルで表されているので、単位をメートルで統一しましょう。
同時に、時速のままでも扱いづらいので、秒速に換算してしまいましょう。
甲:\(\frac{18×10^3}{60×60}=5\)[m/s]
乙:\(\frac{3.6×10^3}{60×60}=1\)[m/s]
車道を横切るタイミングで信号機が赤だった場合は立ち止まらなければなりません。
このため、信号機が赤のときと青のときで甲乙の動き方は変わってきます。
よって、信号機が青であるタイミング(0s〜30s、60s〜90s、……)と赤であるタイミング(30s〜60、90s〜120s、……)に分けて、甲乙それぞれどのように移動していくかを考える必要があります。
以下、スタートからの経過時間を\(t\)[s]と表します。
(i)\(t=0〜30\)(青)のとき
まず甲について、\(t=10\)で車道を通過しますが、信号機は青なので止まることなく進むことができます。
結局、\(t=30\)における甲の位置は、Aから反時計回りに150mだけ進んだ地点になります。
次に乙について、この時間には車道を通過することはなく、\(t=30\)における位置はDから時計回りに30mの地点になります。
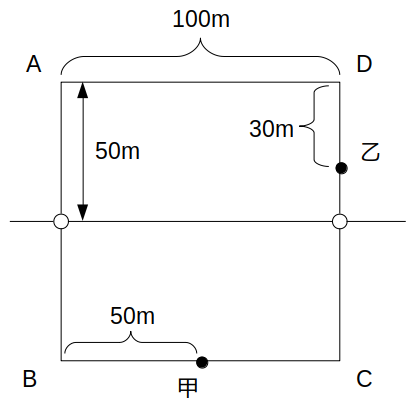
(ii)\(t=30〜60\)(赤)のとき
まず甲について、\(t=50\)で車道を通過しますが、信号機は赤なので停止しなければなりません。
結局、\(t=60\)における甲の位置は、Aから反時計回りに250m進んだ地点(=CD間の信号機)になります。
次に乙について、\(t=50\)でCD間の信号機を通過しますが、信号機が赤のため停止しなければなりません。
このため、\(t=60\)における乙の位置は、Dから時計回りに50mだけ進んだ地点(=CD間の信号機)です。
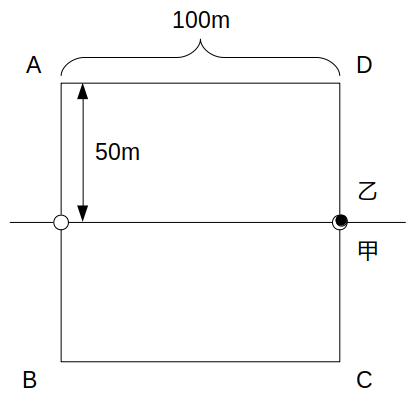
(iii)\(t=60〜90\)(青)のとき
\(t=60\)で信号機が青に変わると、甲と乙は同時にCD間の車道を通過します。(ここで2人は初めて出会い、すれ違います)
まず甲について、この時間では車道を通過することはないので、\(t=90\)における位置はAから反時計回りに400mだけ進んだ地点、すなわちAに戻ります。
次に乙について、こちらもこの時間における車道の通過はなく、\(t=90\)における位置はDから時計回りに80mだけ進んだ地点になります。
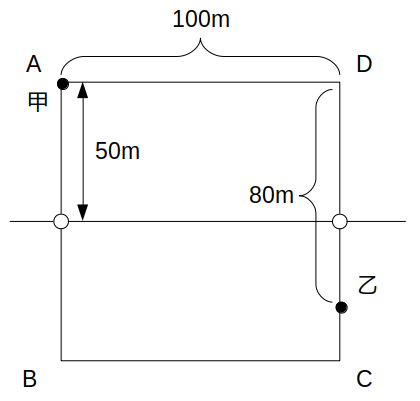
(iv)\(t=90〜120\)(赤)のとき
まず甲について、\(t=100\)で車道を通過しますが、信号機は赤なので停止しなければなりません。
結局、\(t=120\)における甲の位置は、Aから反時計回りに50m進んだ地点(=AB間の信号機)になります。
次に乙について、こちらはこの時間における車道の通過はなく、\(t=120\)における位置はDから時計回りに110mだけ進んだ地点になります。
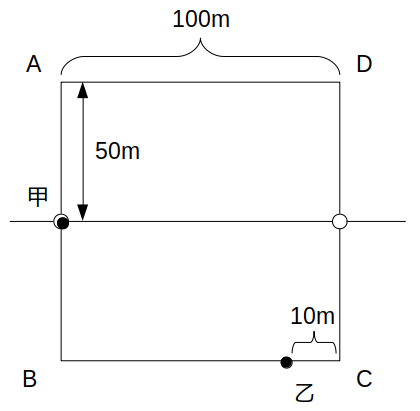
(v)\(t=120〜150\)(青)のとき
まず甲について、\(t=120\)で車道を通過したあとは、この時間における車道の通過はなく、\(t=150\)における位置はAから反時計回りに200mだけ進んだ地点(=C)になります。
これより、\(t=120〜150\)に2人は2回目に出会うことが分かるので、その時間を求めます。
\(t=120\)から甲乙が出会うまでの時間を\(t_1\)とすると、この間に2人が進む距離の合計が140mなので、\(t_1=\frac{140}{5+1}=23\frac{1}{3}\)
スタートから計った時間は、\(120+23\frac{1}{3}=143\frac{1}{3}\)
選択肢のうち、これに最も近いものは2の「2分25秒」ですね。
よって、2が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
逆方向の周回で出会うまでの時間を求める問題でした。
経路の途中に信号機が置かれ、停止する時間も考慮しなければならないところは目新しく感じられたのでは、と思います。
信号機の色によって甲乙の進み方が変わるので、結局はスタートから2人の位置を逐次把握するしかありません。
方針さえ決まれば、あとは手を動かして丁寧に調べるだけです。
計算が複雑な箇所はほとんどないので、状況(赤なのか青なのか)によく注意して手早く処理しましょう。
なお、最初の単位変換は間違いなく行えるようにしてください。
国家総合職の数的処理では、速さの問題は年に1問出るかどうかというところで、頻出というほどではありませんが、可能な限り対策しておくことをおすすめします。
速さをどの程度深く勉強するかは、他の科目や分野の進み具合にもよると思います。
同じ数的処理でも、例えば判断推理なら対応関係の方が確実に優先度は高いので、そういった分野で積み残しがある場合はそちらを優先するのもいいでしょう。
速さに限らないですが、出題頻度が微妙な分野については、参考書で扱うレベルの問題だけさらって、本番で問題を一目見て分からなければスルーする、というスタンスもあるにはあります。
本番が近づいてきたら、全ての分野を網羅するよりも、頻出の分野に絞った勉強の方が効率的な場合もあるので、ある程度勉強が進んだら過去問を見て傾向をつかんでおくのがおすすめです。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
速さの単位を「km/h」から「m/s」に変換する。
甲:\(\frac{18×10^3}{60×60}=5\)[m/s]
乙:\(\frac{3.6×10^3}{60×60}=1\)[m/s]
以下、スタートから経過した時間を\(t\)[s]と表し、信号機が青であるタイミング(0s〜30s、60s〜90s、……)と赤であるタイミング(30s〜60、90s〜120s、……)に分けて甲乙の移動を考える。
(i)\(t=0〜30\)(青)のとき
まず甲について、\(t=10\)で車道を通過するが、青なので止まることなく進めるから、\(t=30\)における甲の位置は、Aから反時計回りに150mだけ進んだ地点となる。
次に乙について、この時間には車道を通過することはなく、\(t=30\)における位置はDから時計回りに30mの地点となる。
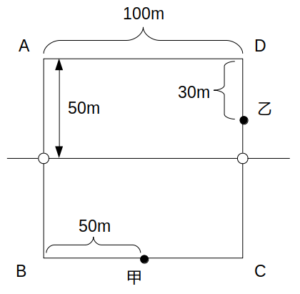
t=30sにおける甲乙の位置
(ii)\(t=30〜60\)(赤)のとき
まず甲について、\(t=50\)で車道を通過するとき、信号機は赤なので停止する。
結局、\(t=60\)における甲の位置は、Aから反時計回りに250m進んだ地点(=CD間の信号機)となる。
次に乙について、\(t=50\)でCD間の信号機を通過するとき、信号機が赤なので停止する。
このため、\(t=60\)における乙の位置は、Dから時計回りに50mだけ進んだ地点(=CD間の信号機)となる。
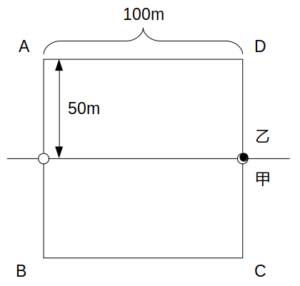
t=60sにおける甲乙の位置
(iii)\(t=60〜90\)(青)のとき
\(t=60\)で信号機が青に変わると、甲乙は初めて出会いすれ違う。
まず甲について、この時間では車道を通過しないので、\(t=90\)における位置はAから反時計回りに400mだけ進んだ地点、すなわちAに戻る。
次に乙について、こちらもこの時間における車道の通過はなく、\(t=90\)における位置はDから時計回りに80mだけ進んだ地点となる。
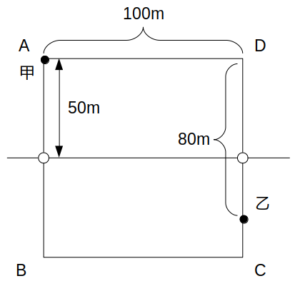
t=90sにおける甲乙の位置
(iv)\(t=90〜120\)(赤)のとき
まず甲について、\(t=100\)で車道を通過するが、信号機は赤なので停止する。
結局、\(t=120\)における甲の位置は、Aから反時計回りに50m進んだ地点(=AB間の信号機)にとなる。
次に乙について、こちらはこの時間における車道の通過はなく、\(t=120\)における位置はDから時計回りに110mだけ進んだ地点となる。
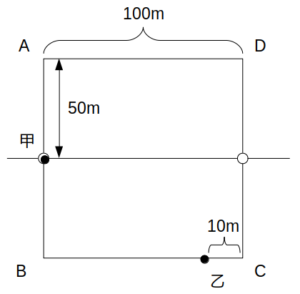
t=120sにおける甲乙の位置
(v)\(t=120〜150\)(青)のとき
まず甲について、\(t=120\)で車道を通過したあと、BC上で乙と2回目に出会うことになる。
\(t=120\)から甲乙が2回目に出会うまでの時間を\(t_1\)とすると、この間に2人が進む距離の合計が140mだから、\(t_1=\frac{140}{5+1}=23\frac{1}{3}\)
スタートから計った時間は、\(120+23\frac{1}{3}=143\frac{1}{3}\)
選択肢のうち、これに最も近いものは2の「2分25秒」である。
よって、正解は2である。

コメント