こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
コロナでしばらく閉店していた近所のラーメン屋さんが復活したので、早速行ってきました。
前から行きつけだったので、閉店したときは少々残念な気持ちでしたが、無料で大盛りにしてくれるサービスの良さは健在でした。
感染者数が減る中、宣言も解除されて、少しずつ戻りつつある日常を実感できるとうれしい気持ちになりますね!
前回は、道幅の狭い陸上トラックで2人の走者が正面衝突するまでの時間を求める問題をやりました。
問題の内容と解法の流れを、今、なんとなくでいいので思い出してみましょう。
どうしても思い出せない箇所があるとか、はたまた完全に忘れてしまったという方は、簡単にでもいいので早いうちに復習しておくことをおすすめします。
数的処理に限らず、勉強した内容はあまり時間を置かずに見返すと、定着しやすくなりますよ。
「思い出す」というプロセスによって、人の記憶はしだいに定着していきます。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
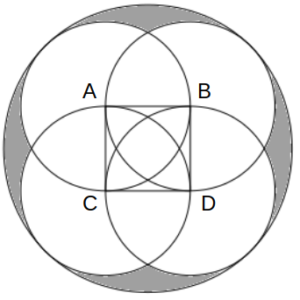
図のように、正方形ABCDの4頂点を中心とする小円を描き、それら4つの小円に外接するように大円を描く。正方形ABCDの1辺の長さおよび小円の半径を1とすると、灰色で示される領域の面積はいくらか。
- \((\sqrt{2}+\frac{5}{12})\pi -2-\sqrt{3}\)
- \((2\sqrt{2}+\frac{1}{4})\pi -2-\sqrt{2}\)
- \((\sqrt{3}+\frac{1}{2})\pi -1-\sqrt{3}\)
- \((\sqrt{3}-\frac{3}{4})\pi -2+\sqrt{3}\)
- \((\sqrt{2}-\frac{1}{10})\pi -1-\sqrt{3}\)
5
4つの小円に外接する大円を描き、隙間にあたる領域の面積を求める問題です。
図形の問題では補助線を引くのが定番ですが、どんな補助線を引いたらいいでしょう?
以下で詳しく解説します。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこまで読み飛ばしても問題ありません。
それではスタート!
詳しい解説
次図のように補助線GHを引くと、GHは大円の直径で、点A、CはGH上にあります。
また、次図のように2つの三角形ABEおよびADFを描くと、各辺は全て小円の半径1で等しいから、これらはともに正三角形です。
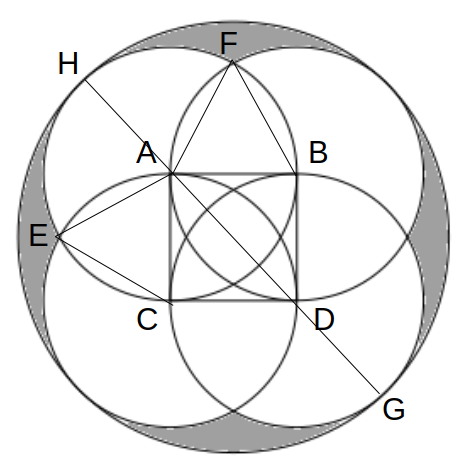
図形の対称性より、灰色の領域の面積は次のように求められます。
\[
(灰色領域)=(大円)-(扇形\mathrm{AEHF})×4-△\mathrm{ABF}×4-(正方形\mathrm{ABCD})
\]
まず扇形AEHFの面積ですが、半径は1なので、あとは中心角が分かれば求められますね。
中心角∠EAFは、\(∠\mathrm{EAF}+∠\mathrm{BAE}+∠\mathrm{DAF}+∠\mathrm{BAD}=360^\circ\)
より、\(∠\mathrm{EAF}=360^\circ – 60^\circ – 60^\circ – 90^\circ=150^\circ\)
よって、\(扇形\mathrm{AEHF}=\pi × 1^2× \frac{150^\circ}{360^\circ}=\frac{5}{12}\pi\)
次に、△ABFの面積を求めましょう。
1辺の長さが1の正三角形の高さは\(\frac{\sqrt{3}}{2}\)なので、面積は次のように求められます。
\[
△\mathrm{ABF}=\frac{1}{2}×1×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}
\]
あとは大円の面積ですが、GHは半径2つ(AHとCG)と正三角形の対角線(AC)の和だから、\(2+\sqrt{2}\)
よって半径は\(1+\frac{\sqrt{2}}{2}\)なので、\((大円の面積)=\pi ×(1+\frac{\sqrt{2}}{2})^2=\)
以上より、灰色の領域の面積は次のように求められます。
\[
(1+\frac{\sqrt{2}}{2})^2\pi-\frac{5}{12}\pi×4-\frac{\sqrt{3}}{4}×4-1^2=(\sqrt{2}-\frac{1}{10})\pi -1-\sqrt{3}
\]
したがって、5が正解となります。
おわりに
お疲れ様でした!
いかがだったでしょうか?
直径GHを補助線として導入しさえすれば、あとは簡単な図形の面積を求めるだけで解けましたね。
逆に、GHを引くことができず、手も足も出なかった方も多いのではないでしょうか。
その意味で、すらすらと解けた方と手が止まってしまった方で二極化しやすい問題だったと思います。
本試験なら、まさに合否の分かれ目となる問題といえます。
そうはいっても、解けなかった方もあまり落ち込まないで大丈夫です。
全部で14問もある数的処理のうちのたった1問ですから、この問題が解けなかったからといって不合格とはなりません。
教養試験全体で見れば30問のうちの1問ですから、できなくても他でカバーすれば十分合格できます。
日頃の勉強でできない問題をなくす心がけは重要ですが、神経質になりすぎるのもよくありません。
例えば今回のような図形問題がどうしても苦手であれば、切り捨てて他の分野なり、科目なりを底上げするのも一つの作戦ですよ!
ぜひ本サイトを活用して、数的処理全体で高得点を出すことを意識して勉強してみてください。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
次図のように大円の直径GHを引くと、点A、CはGH上にある。
また、2つの三角形ABEおよびADFを描くと、各辺は全て小円の半径1で等しいから、これらはともに正三角形である。
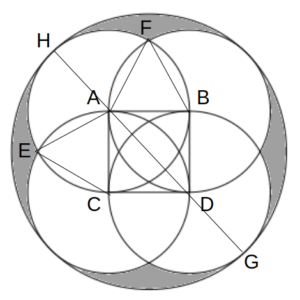
補助線GHを記入
\[
(灰色領域)=(大円)-(扇形\mathrm{AEHF})×4-△\mathrm{ABF}×4-(正方形\mathrm{ABCD})
\]
まず、扇形AEHFの面積を求める。
中心角∠EAFは、\(∠\mathrm{EAF}+∠\mathrm{BAE}+∠\mathrm{DAF}+∠\mathrm{BAD}=360^\circ\)
であるから、\(∠\mathrm{EAF}=360^\circ – 60^\circ – 60^\circ – 90^\circ=150^\circ\)
よって、\(扇形\mathrm{AEHF}=\pi × 1^2× \frac{150^\circ}{360^\circ}=\frac{5}{12}\pi\)
次に、△ABFの面積を求める。
1辺の長さが1の正三角形の高さは\(\frac{\sqrt{3}}{2}\)なので、面積は次式で求められる。
\[
△\mathrm{ABF}=\frac{1}{2}×1×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}
\]
さらに、大円の面積を求める。
GHは半径2つ(AHとCG)と正三角形の対角線(AC)の和だから、\(2+\sqrt{2}\)
よって半径は\(1+\frac{\sqrt{2}}{2}\)であるから、\((大円の面積)=\pi ×(1+\frac{\sqrt{2}}{2})^2=\)
以上より、灰色の領域の面積は次のように求められる。
\[
(1+\frac{\sqrt{2}}{2})^2\pi-\frac{5}{12}\pi×4-\frac{\sqrt{3}}{4}×4-1^2=(\sqrt{2}-\frac{1}{10})\pi -1-\sqrt{3}
\]
よって、正解は5である。

コメント