【国家総合職】公務員試験の線型計画法は正攻法で解いてはいけません【外注にかかる手数料の最小値】

こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます！
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。

私は暑がりなので、今頃の時期でも割と長袖の下に半袖のTシャツを着て出かけるんです。
そのことを職場で話したらメッチャ驚かれました。
建物内では暖房があるし、ちょっと歩くだけでも結構汗が出るので、半袖＋長袖くらいの服装がちょうどいいんですよね。

決まった条件の下で利益や生産数を最大化したい、という問題は数的処理にありがち。
そんな最大・最小に関する問題を解くための手法としてメジャーなのが「線型計画法」です。
なんだか難しそうな名前ですが、解き方は固定化されているので、きちんと対策すれば確実に得点できます。
与えられた条件をもとに不等式を作って、グラフにするだけです。

ただ、この「グラフにする」というのが厄介で、正解を得るには傾きや切片の大小をある程度正確に描かなくてはなりません。

不等式を作るだけならまだしも、グラフ化までやると結構な時間がかかってしまいます。
時間設定のシビアな数的処理を攻略する上で、これは致命的です。
線型計画法の問題をまともに解くのはオススメできません。

しかし、安心してください。
線型計画法には抜け道があります。

この記事では、公務員試験の数的処理では定番の線型計画法を扱った問題を最短で解くための「解法のポイント」を紹介します。
それから過去問の類題を一緒に解いて理解していただくことで、本番で使える解法を身につけていってもらいます！

講義：線型計画法の時短攻略法

線型計画法の時短攻略法を伝授！

条件を満たす領域内を動く直線を図示して最大・最小を調べる、というのが正攻法ですが、公務員試験でこれをやっている時間はありません。
数的処理は選択式ですから、条件を満たす点\((x,y)\)が必ずただ一つに決まります。
加えて、条件を満たす領域は九分九厘多角形です。

多角形で特徴的な点といえば、それは頂点しかありません。
であれば、頂点をすべて代入して、直接大小を比べちゃえばいい、というわけになります。

(例題)
ある動物は炭水化物とタンパク質については、一定期間にそれぞれ700ｇ以上,400ｇ以上摂取しなければならない、と仮定しよう。
2種類の飼料AとBがあり、それぞれ1単位に含まれる栄養素の含有量,及び単位あたりの価格が次の表によって与えられている。

(1)各栄養素の最小必要量以上を確保した上で、その総費用を最小にするには、A,Bを何単位(整数単位とする)与えるのがよいか。

（答）

与えるA,Bの単位数をx,yとすると、条件より

x+2y≧700, x+y≧400, x≧0, y≧0

これらの不等式を満たすx,yについて、総費用 11x+12yが最小となるときを考える。
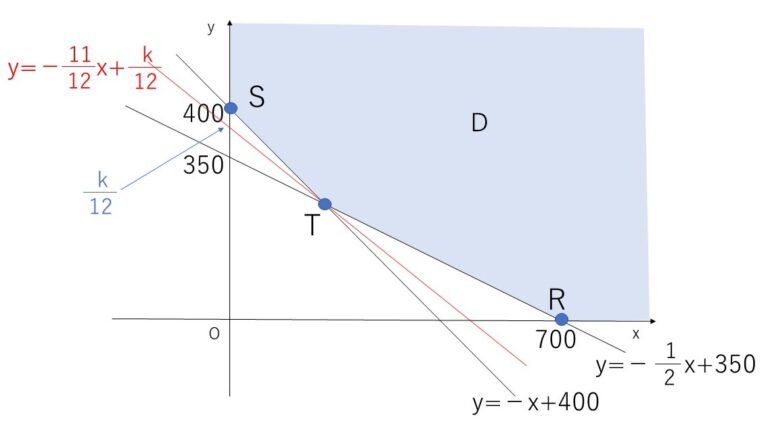
11x+12y=k・・・① とおくと、①はy=−1112x+k12。

不等式の表す領域Dと①が共有点をもつうち\(\frac{k}{12}\)(直線①のy切片)が最小となるときは図のTを通るときで、このときkも最小。

x+2y=700, x+y=400 の交点Tの座標は、T(100,300)

したがって費用が最小となるのは x=100,y=300 のとき(ともに整数値となる)。

答え Aを100単位, Bを300単位

線型計画法(文章問題) | 教えて数学理科

演習問題：外注にかかる手数料の最小値

いくつかの条件の中で手数料を最小化する問題です。
具体的な数値が問われているので、数式を使って考える必要があります。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。

それではスタート！

解説

「〜以上」とか「〜以内」という条件が複数あるところから、「線形計画法が使えないかな？」と当たりをつけます。

「1日あたりの」という表現が多く登場することから、XとYの稼働日数をそれぞれ\(x\)、\(y\)とおいて条件を数式で表してみます。
提示された条件は、「Aを300個以上」「Bを400個以上」「自社工場で製造した場合に比べた1日あたりの工賃の増加額を192000円以内に」の3つです。

まず、Aについての条件を数式で表すと、\(10x+15y≧300\)
すなわち、\(y≧-\frac{2}{3}x+20\)

Bについては、\(20x+10y≧400\)
すなわち、\(y≧-2x+40\)

さらに、自社工場で製造した場合に比べた工賃の増加額について、\(4800x-4800y≦192000\)
すなわち、\(y≧x-40\)

また、手数料について、\(72000x+48000y=48000k\)とおくと、\(y=-\frac{3}{2}x+k\)

以上を\(xy\)平面上に図示すると、以下のようになります。

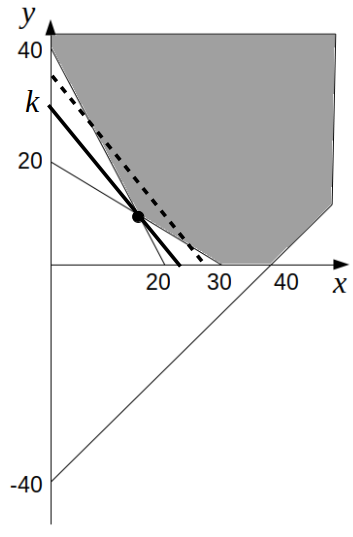
線形計画法の考え方より、手数料（＝\(k\)）が最小となるのは、2直線\(y=-\frac{2}{3}x+20\)と\(y=-2x+40\)の交点\((15, 10)\)を通るときであると分かります。

このとき、手数料は\((72000×15+48000×10=1560000\)円となります。

よって、４が正解です。

おわりに

お疲れ様でした！
いかがだったでしょうか？

線型計画法は、境界線の交点にのみ注目すればOKです。

「〜以上」とか「〜以内」という条件が複数ある場合は、線形計画法の活用を検討しましょう。
この手法それ自体が一つの独立した解法みたいなものなので、気づいてしまえばあとはいかに早く処理するか、ということが問題になります。
線形計画法で解く問題だと分かったら、境界となる直線の交点を全て求めて代入し、得られた値の中から最大値（あるいは最小値）を選ぶ、というやり方が有効です。
この方が機械的に解けますし、何より図を描く手間が省けるので時間を大幅に節約できます。
下の「略解」には、こっちの解き方を載せています。

他の問題にも言えることですが、数的処理は時間勝負なので、こうやって少しでも時間を節約できるアイデアを持っておくのはかなり重要です。
日頃の問題演習では、解説を読んでその通りに理解するのはもちろん大切ですが、一方で自分なりの抜け道を探すことにもチャレンジしましょう。

最後までお読みいただきありがとうございました！

本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします！

次回もお楽しみに！

略解