こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
今回のテーマは「面積」です。
面積の問題に対する解法は2パターンあります。
以下の記事で、面積の問題の解き方を詳しく書いているので、まだ見てない方はぜひ覗いてみてください。

まだ見てない方は、先にこっちを見ると理解しやすいかも
演習問題:共通接線と面積
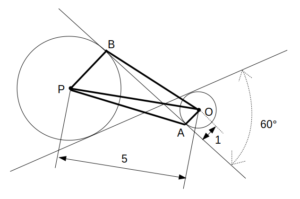
図のように、点Oおよび点Pを中心とする2つの円に対し、2本の共通接線を引き、接点をそれぞれ点Aおよび点Bとする。点Oを中心とする円の半径が1、中心間の距離が5、2本の共通接線のなす角度が60°であるとき、四角形OAPBの面積はいくらか。
- \(\frac{4\sqrt{3}}{3}\)
- \(\frac{13\sqrt{3}}{4}\)
- \(\frac{18\sqrt{3}}{5}\)
- \(\frac{25\sqrt{3}}{8}\)
- \(\frac{35\sqrt{3}}{8}\)
4
共通接線と面積の問題です。
面積といえば公式か相似比ですが、今回はどちらのパターンでしょう?
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
平面図形の面積を求める方法は2通りでしたね。
- 大きさが分かっている図形との相似比から求める方法
- 具体的に長さを求めて面積公式に当てはめる方法
本問の場合、求めたい四角形OAPBと相似な図形は見当たりません。
四角形OAPBを三角形に分割したとしても、相似の関係だけで面積を知るのはどうも難しそうです。
そこで、本問は2の面積公式による方法を使って解く方針でいきます。
四角形OAPBってどんな形?
面積の公式を使う場合、四角形OAPBが何者か(=平行四辺形なのか台形なのか)を知る必要があります。
そこで、まずは四角形OAPBの形状を調べます。
直線ABは円Oおよび円Pの両方に接するので、OA⊥ABかつPB⊥AB
よって、OA//PB
これより、四角形OAPBは台形であることが分かります。

OAが上底でPBが下底、ABが高さだね
OA=1なので、あとはPBとABの長さが分かれば、台形の面積の公式が使えますね。
次は、この2つを明らかにしていきます。
ジグソーパズルってありますよね。
記憶力や細部への注意力が向上したり、ストレス解消になったりする効果があるそうです。
今回は、そんなジグソーパズル「っぽい」問題を紹介します↓
\\\【模様のある紙片の並べ方】///
過去に本試験で出題された問題の改題です。
演習問題ではありますが、遊び感覚で挑戦してみてください。
Twitterもよろしくね!↓
辺の長さを調べて面積の公式を使う
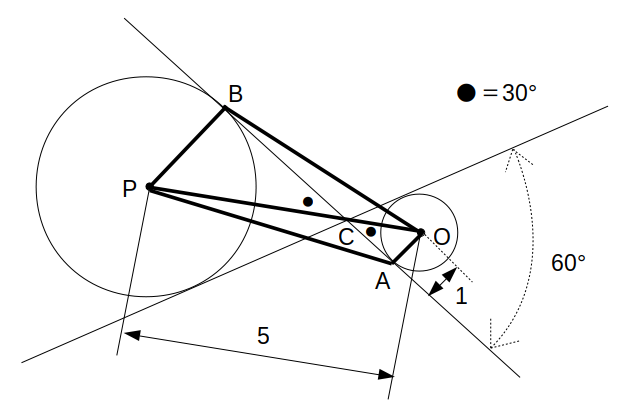
2本の共通接線の交点をCとすると、∠OCA=∠PCB=30°
よって、△OACおよび△PBCはともに\(1:2:\sqrt{3}\)の直角三角形です。
OA=1なので、OC=2、AC=\(\sqrt{3}\)
これより、PC=5−2=3
すると、PB=\(\frac{3}{2}\)、BC=\(\frac{3\sqrt{3}}{2}\)
よって、AB=\(\sqrt{3}+\frac{3\sqrt{3}}{2}=\frac{5\sqrt{3}}{2}\)

これで必要な材料はそろったね
以上より、\((四角形\mathrm{OAPB})=\frac{\mathrm{OA}+\mathrm{PB}}{2}×\mathrm{AB}=\frac{1+\frac{3}{2}}{2}×\frac{5\sqrt{3}}{2}=\frac{25\sqrt{3}}{8}\)
よって、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
面積の問題は、相似か面積公式、どちらかで解けます。
共通接線をテーマにした面積の問題でした。
面積の問題を見たら、公式か相似比か、いずれを用いるパターンなのかを見極めましょう。
前者であれば線分の長さを求めるのが目標になりますし、後者なら相似の関係にある図形を探す必要があります。
本問は相似の関係では解決できないので、四角形OAPBが台形であることを見抜いて、公式を利用することになります。
OPが共通接線の成す角(60°)を二等分することは、知識として知っておきましょう。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
直線ABは円Oおよび円Pの両方に接するから、OA⊥ABかつPB⊥AB
よって、OA//PB
これより、四角形OAPBは台形である。
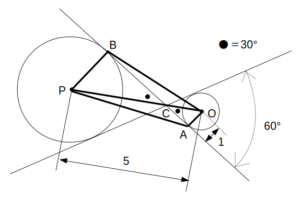
PBとABの長さを求める
2本の共通接線の交点をCとすると、∠OCA=∠PCB=30°
よって、△OACおよび△PBCはともに\(1:2:\sqrt{3}\)の直角三角形である。
OA=1より、OC=2、AC=\(\sqrt{3}\)
これより、PC=5−2=3
すると、PB=\(\frac{3}{2}\)、BC=\(\frac{3\sqrt{3}}{2}\)
よって、AB=\(\sqrt{3}+\frac{3\sqrt{3}}{2}=\frac{5\sqrt{3}}{2}\)
以上より、\((四角形\mathrm{OAPB})=\frac{\mathrm{OA}+\mathrm{PB}}{2}×\mathrm{AB}=\frac{1+\frac{3}{2}}{2}×\frac{5\sqrt{3}}{2}=\frac{25\sqrt{3}}{8}\)
したがって、4が正解である。

コメント