こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
雨上がりの道路に射す日差しが好き。
前回は、いくつかの推論が正しいかどうかを検討する問題をやりましたね。
国家総合職でほぼ毎年出題されている推論の問題に対する基本的な対処法が分かる内容なので、解いてない方はぜひ挑戦してみてください。
もう解いた方は、要点だけでも早めに復習しておくようにしましょう。
新しい問題を解いたら、少し時間をおいてから解法の流れをもう一度頭の中で再現してみる、ということをするのがおすすめです。
あまり時間が経つと要点すらも忘れてしまい、思い出すのも難しくなってしまいます。
そうなるとまた一から解答を読まなければならず、非常に面倒ですよね。
だからこそ、かすかに残っている記憶を呼び戻す、というのが最も効率の良い勉強法になります。
ぜひ、思い出す勉強法を日々の習慣に取り入れてみてください。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
ある商社では、繁忙期である来月を乗り切るための対策として、2人の社員A、Bに残業させる計画を立てている。AとBが1時間仕事したときに発生する給与、処理できる仕事の件数、得られる新規顧客の数はそれぞれ表の通りである。AとBが1ヶ月残業したことにより発生する給与は合計で8万円以内、処理すべき仕事の件数は36件以上、残業時間の合計は50時間以内とするとき、得られる新規顧客の人数は最大でいくらか。
| 給与 | 処理できる仕事 | 得られる新規顧客 | |
| A | 1500円 | 0.8件 | 0.3人 |
| B | 2000円 | 1.2件 | 0.2人 |
- 7.5人
- 9.8人
- 10人
- 12.5人
- 14人
5
与えられた条件のもとで新規顧客を最大化する問題です。
問題にある通り、件数や人数は整数とは限りません。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
いくつかの数値的な条件のもとでの最大・最小を求めるには、「線形計画法」が有効です。
まずはAとBの残業時間をそれぞれ\(x, y\)とおいて、条件を定式化しましょう。
条件「残業したことにより発生する給与は合計で8万円以内」を数式で表すと、次のようになります。
\(1500x+2000y≦80000\)
整理すると、\(y≦-\frac{3}{4}x+40\)・・・(i)
次に、条件「処理すべき仕事の件数は36件以上」を数式化すると、次の不等式が得られます。
\(0.8x+1.2y≧36\)
整理すると、\(y≧-\frac{2}{3}x+30\)・・・(ii)
さらに、条件「残業時間の合計は50時間以内」を数式化すると、次の不等式が得られます。
\(x+y≦50\)
すなわち、\(y≦-x+50\)・・・(iii)
これらのもとで、得られる新規顧客の人数を\(2k\)とおき、これを最大化しましょう。
新規顧客の人数は、\(2k=0.3x+0.2y\)
すなわち、\(y=-\frac{3}{2}x+10k\)・・・(※)
(あとで\(y\)の係数で割ることを想定し、\(k\)ではなく\(2k\)とおきました)
以上、不等式(i)、(ii)、(iii)、および等式(※)を\(xy\)平面上に図示すると次のようになります。
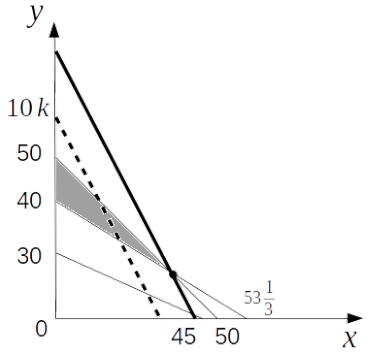
不等式(i)、(ii)、(iii)を全て満たす領域は図の灰色で示された部分になります。
「条件を満たす」とは、\(xy\)平面上では太字の直線(※)が灰色の領域と共有点を持つこと、と言い換えられます。
直線(※)が灰色の領域と共有点を持ちながら平行移動する場合、切片である「\(k\)」が最大となるのは、図のように2直線\(y=-\frac{3}{4}x+40\)と\(y=-x+50\)の交点を通るときです。
2直線\(y=-\frac{3}{4}x+40\)と\(y=-x+50\)の交点を求めると、\((x, y)=(40, 10)\)
このとき、新規顧客の数は\(2k=0.3×40+0.2×10=14\)人となります。
したがって、5が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
線形計画法により最大値を求める問題でした。
線形計画法を使った解法は、制約条件を不等式(\(y=〜\)の形)で表したあと、\(xy\)平面上に不等式が表す領域を図示し、直線の切片が最大(最小)となるのはどんなときかを検討することになります。
…というのが正式な手順ですが、数的処理でこの手順をそのまま適用するのは得策ではないと私は思います。
というのも、線形計画法では図示した領域の頂点が最大値(最小値)を与えるポイントとなるケースが圧倒的に多いのです。
であれば、線形計画法を使うと判断した時点で、領域の頂点の座標(多くは直線の交点)だけ集めて全て代入し、具体的に値を比較する方が早いように思われます。
正しければ選択肢のどれかにたどり着きますから、それをマークしてその問題はおしまいです。
数的処理では領域を図示するのも手作業になりますが、直線の傾きや切片などをある程度正しく描かないと、図形的な考察がうまくできません。
そのような手間を考えると、領域の頂点の座標だけ押さえて具体的な値を求め、比較する方が機械的にできる分、容易に解答を得られると思いませんか?
もちろん、この方法では図形的な考察をカットしているので不安は残るでしょうが、時間に限りのある本番という条件下では、ある程度信頼性のある解答を得られるだけでも十分に価値があります。
数的処理では、100%自信のある解答を1つ用意するより、70〜80%程度の完成度で出した解答3つの方が、高得点にはつながりやすいです。
本番でこれを実践するかどうかはお任せしますが、抜け道の一つとして知っておくのは悪くないと思います。
こんな解き方、市販の書籍には絶対に載せられませんね。
こうした裏技的な解法を公開できるのも、また個人ブログのメリットだと思います。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
AとBの残業時間をそれぞれ\(x, y\)とおく。
条件「残業したことにより発生する給与は合計で8万円以内」より、
\(1500x+2000y≦80000\)
すなわち、\(y≦-\frac{3}{4}x+40\)・・・(i)
条件「処理すべき仕事の件数は36件以上」より、
\(0.8x+1.2y≧36\)
すなわち、\(y≧-\frac{2}{3}x+30\)・・・(ii)
条件「残業時間の合計は50時間以内」より、
\(x+y≦50\)
すなわち、\(y≦-x+50\)・・・(iii)
得られる新規顧客の人数を\(2k\)とおくと、\(2k=0.3x+0.2y\)
すなわち、\(y=-\frac{3}{2}x+10k\)・・・(※)
不等式(i)、(ii)、(iii)、および等式(※)を\(xy\)平面上に図示すると次のようになる。
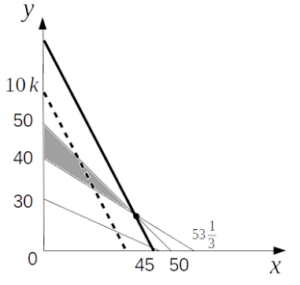
線形計画法による最大化
不等式(i)、(ii)、(iii)を全て満たす領域は図の灰色で示された部分である。
\(xy\)平面上で、太字の直線(※)が灰色の領域と共有点を持つように平行移動する場合、切片(得られる新規顧客の人数)が最大値を取るのは、2直線\(y=-\frac{3}{4}x+40\)と\(y=-x+50\)の交点を通るときである。
2直線\(y=-\frac{3}{4}x+40\)と\(y=-x+50\)の交点は、\((x, y)=(40, 10)\)
このときの新規顧客の数は\(2k=0.3×40+0.2×10=14\)人
以上より、正解は5である。

コメント