こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
「確率・場合の数」といえば、頻出なのにもかかわらず苦手意識を持つ方も少なくない、数的処理の鬼門です。
事象のカウントに分数の約分……
少しのミスが誤答につながります。

筆者も同じのを2回数えたり、ケアレスミス多かったなー
正答を導き出すには、樹形図や和の法則、積の法則といった道具から適切な解法を選び出す必要があります。
苦手な方には、そもそも適切な解き方を選ぶことも難しいかもしれません。
今回は、「確率・場合の数」で頻出の解法のパターンを紹介します。
後半は過去問の類題を一緒に解いて理解してもらい、本番で使える解き方を身につけていってもらいます!
- 講義:確率(&場合の数)の解き方5パターン
- 演習問題:トーナメントの決勝戦に勝ち残る確率
- 解説:定義からでも、確率からでも
- 入れ子構造の場合分け
- (a1)Aが3回戦まで勝つ確率→\(\frac{1}{36}\)
- (b2)Bが3回戦まで勝つ確率→\(\frac{1}{30}\)
- (b3)Bが3回戦まで勝つ確率→\(\frac{2}{15}\)
- Bが勝つ確率:排反事象の足し算
- (A,B)の確率→\(\frac{1}{180}\):独立事象のかけ算
- (a2)(A,B)の確率→\(\frac{1}{180}\):a1と同じ
- (a3)Aが3回戦まで勝つ確率→\(\frac{1}{9}\)
- b1〜b3は同じ→Bの確率=\(\frac{1}{5}\)
- (A,B)の確率:a1〜a3は排反
- (□, □)のパターン数=A〜Fから2個取る順列
- 別解:定義からも確率を求められる
- おわりに:「数え上げて定義」か「確率から確率」か
- 略解
講義:確率(&場合の数)の解き方5パターン
確率(と場合の数)の問題は、次の5通りの解法を頭に入れておけばOKです。
-
事象をカウントし定義から求めるやり方
- 樹形図や書き出しによる数え上げ
- 組み合わせや順列を使った計算
-
確率から確率を求めるやり方
- 排反事象の足し算(和の法則)
- 独立事象のかけ算(積の法則)
- 全体から引く(余事象の確率)
これらの方法は、いずれか一つで解ける場合もありますが、複雑な問題だといくつか組み合わせて解くことになります。
事象をカウントし定義から求めるやり方
【1】樹形図や書き出しによる数え上げ
条件に合う事象をひたすら列挙して数え上げる、ちょっと力技な解法です。
両手で数えられる程度のパターン数を扱うケースや、途中で分岐を生じるような場合に有効です。
順番を気にするなら樹形図、順番ではなくグループ(組み合わせ)が問題なら書き出しを使うと解ける傾向があります。
(問)
(答)
【確率】問題2 | 公務員試験数的処理解法テクニック KOMARO
上の例題では、最も長い辺が4〜6のいずれかに限られることに着目し、全パターンを数え上げてます。

最大の整数が4〜6なら、せいぜい\({}_5\mathrm{C}_2=10\)通り
順番ではなく「組」が重要なことから、書き出しによる方法が有効です。
({6,5,4}も{6,4,5}も{5,6,4}も同じ)
樹形図を書いて考えてもOKです。
【2】組み合わせや順列を使った計算
組み合わせや順列を使って機械的にカウントする方法もあります。
扱う事象が多すぎる場合に有効です。
書き出しても書き出してもキリがないときは、このやり方を検討してみてください。
ちなみに、確率の分母はほぼほぼこの方法で求めることになります。

何十通り、何百通りもある全事象を書き出すのはさすがにキビシイ
(問)
(答)
【確率】問題1 | 公務員試験数的処理解法テクニック KOMARO
上の例題では、余事象を経由して確率を求めてます。
17本のはずれくじ(a,b,c,d,e,…)から2本を取り出すときの取り出し方は、
(a,b)、(b,c)、(b,e)、(c,e)、……
と、ちょっと考えただけでもたくさん出てきます。
こういうケースは、(答)にもあるように、組み合わせの考え方を活用するのが正解です。
確率から確率を求めるやり方
以下の解き方は、既知の確率から別の事象の確率を求めるときに有効です。

3回コインを投げて表が2回出る確率、とかね(表の確率は1/2で既知)
【3】排反事象の足し算(和の法則)
2つの事象AとBが同時に起こらない(=排反事象である)場合、「AまたはB」の確率はAの確率とBの確率の足し算で求められます。
……というのが、和の法則です。
実戦的には、排反なケース(AとB)に場合分けしたあと、それらを足し合わせて「AまたはB」の確率を求める、という使い方をします。
【4】独立事象の掛け算(積の法則)
2つの事象AとBがあって、これらが互いに影響し合わずに起こる(=独立事象である)とき、「AかつB」の確率はAの確率とBの確率の掛け算で求められます。
……これが、積の法則です。
実戦的には、AかつBの確率を直接求めるのが難しいときに、「Aの確率」と「Bの確率」を別々に求めて掛け合わせる、という使い方をします。
【5】全体から引く(余事象の確率)
Aが起こる確率は、「全事象の確率(=1)」から「Aが起こらない確率」を引くことでも求められます。
「少なくとも〜」という表現を見たら、このやり方です。
(問)
ある高速道路にはA、B、Cのインターチェンジがこの順に並んでおり、
AB間とBC間を通るときに渋滞に遭う確率はそれぞれ0.3と0.2である。A~
Cまで高速道路を走行するとき、AB間とBC間の少なくとも一方で渋滞に遭
う確率はいくらか。
1. 0.34
2. 0.39
3. 0.44
4. 0.49
5. 0.54(答)
「1-渋滞に遭わない確率」で考えればよい。
公務員試験過去問 数的推理 確率 | 問題野郎
よって「1 - (0.7×0.8)=0.44」となる。
上の例題は、和の法則と余事象、両方を使って解いてます。
「少なくとも一方で〜」という表現があるので、余事象の確率(=ABとBCでいずれも渋滞に遭わない確率)が有効です。
さらに、「ABで渋滞に遭わない」という事象と、「BCで渋滞に遭わない」という事象は互いに影響し合わない(=独立事象)ので、余事象の確率は「ABで渋滞に遭わない確率」と「BCで渋滞に遭わない確率」の積となります。
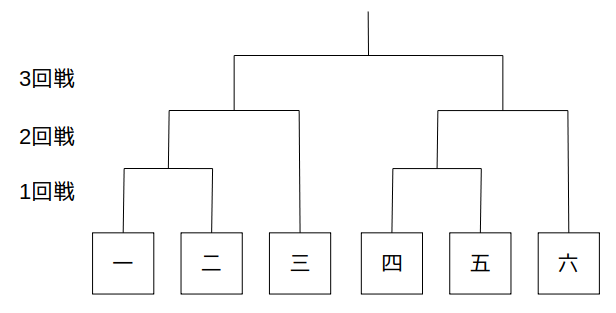
演習問題:トーナメントの決勝戦に勝ち残る確率
あるスポーツの大会に参加する6チームA〜Fが、次図に示すトーナメント表にしたがって勝敗を競うことになった。各チームの配置(「一」から「六」のいずれか)は、くじ引きにより無作為に決められる。各チームは実力が伯仲しており、一方が他方に勝利する確率および敗北する確率はともに\(\frac{1}{2}\)である。ただし、2回戦のみ、「三」(または「六」)のチームがそれぞれ対戦相手に勝つ確率は\(\frac{2}{3}\)、負ける確率は\(\frac{1}{3}\)であるとする。
このとき、AとBのいずれか一方でも3回戦まで勝ち残る確率はいくらか。
- \(\frac{3}{4}\)
- \(\frac{2}{5}\)
- \(\frac{3}{5}\)
- \(\frac{4}{9}\)
- \(\frac{8}{15}\)
3
トーナメント戦で特定のチームが勝ち残る確率の問題。
気づけば早い。
以下、詳しい解説。
回りくどい説明が嫌な方は、一番下の略解を見てね。
それでは、解説スタート!
解説:定義からでも、確率からでも
本問は、「3回戦で対戦するのはどのチーム?」が争点。
経緯はどうあれ、3回戦のチームが結果として「A または B」であればよいわけです。
ゴールからの逆算で考えてみます。
先にゴール(3回戦の対戦チーム)を決めておき、その状態に至る確率を調べる、という順番です。

×(パターン数)すれば求める確率になるね
以下、例として3回戦の対戦チームを(A,B)に決め、そうなる確率を求めます。
-
事象をカウントし定義から求めるやり方
- 樹形図や書き出しによる数え上げ
- 組み合わせや順列を使った計算
-
確率から確率を求めるやり方
- 排反事象の足し算(和の法則)
- 独立事象のかけ算(積の法則)
- 全体から引く(余事象の確率)
入れ子構造の場合分け
3回戦が(A,B)であるためには、AとBが左右別々のブロックにいることが前提になります。
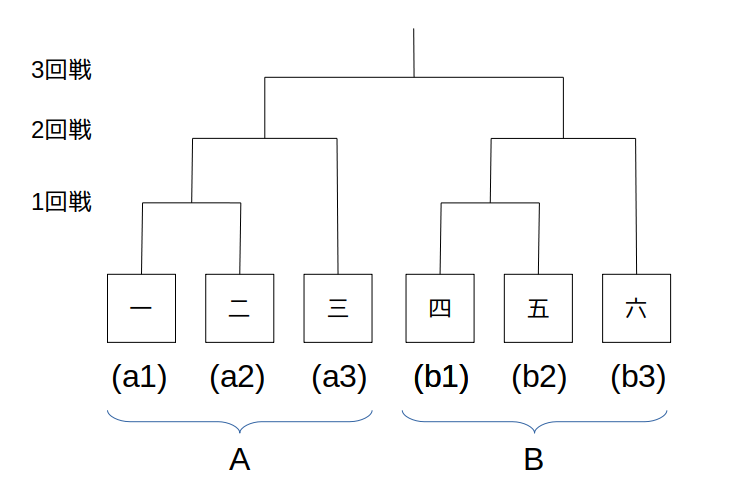
Aの場所(a1〜a3)一つ一つに対し、Bの場所は3通り(b1〜b3)ずつ。
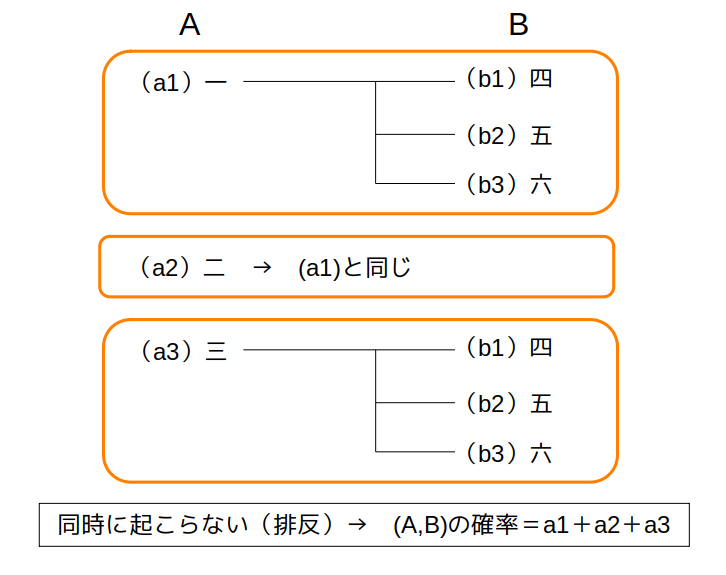
b1〜b3は同時に起こらない(=排反)ので、
a1の確率:b1+b2+b3
さらに、a1〜a3も同時に起こらない(=排反)ので、
(A,B)の確率:a1+a2+a3

a1〜a3のそれぞれにb1+b2+b3がぶら下がってる
(a1)Aが3回戦まで勝つ確率→\(\frac{1}{36}\)
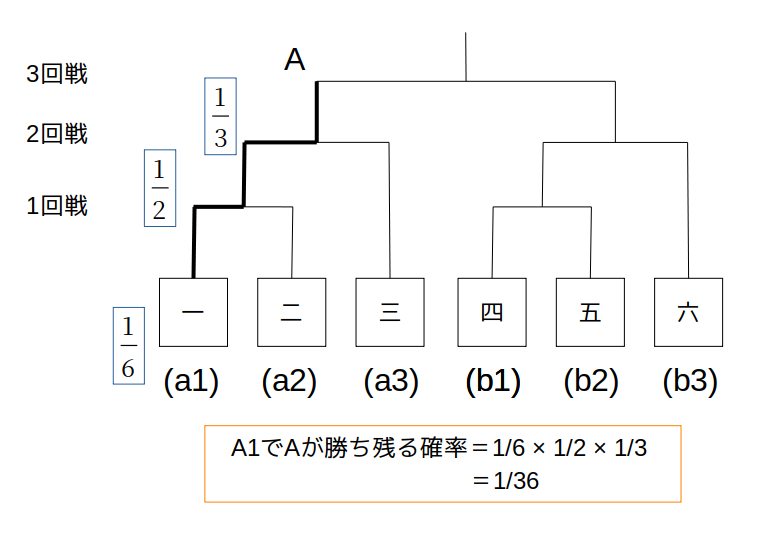
くじ引きでAが「一」になる確率は\(\frac{1}{6}\)
このとき、Aが勝つ確率は、
なので、
\(\frac{1}{2}×\frac{1}{3}=\frac{1}{6}\)
よって、A=a1で勝ち残る確率は、
\[
\frac{1}{6}×\frac{1}{6}=\frac{1}{36}
\]

勝つ、かつ、……カツ??
ここからは、b1〜b3それぞれでBが勝つ確率を考えます。
(b1)Bが3回戦まで勝つ確率→\(\frac{1}{30}\)
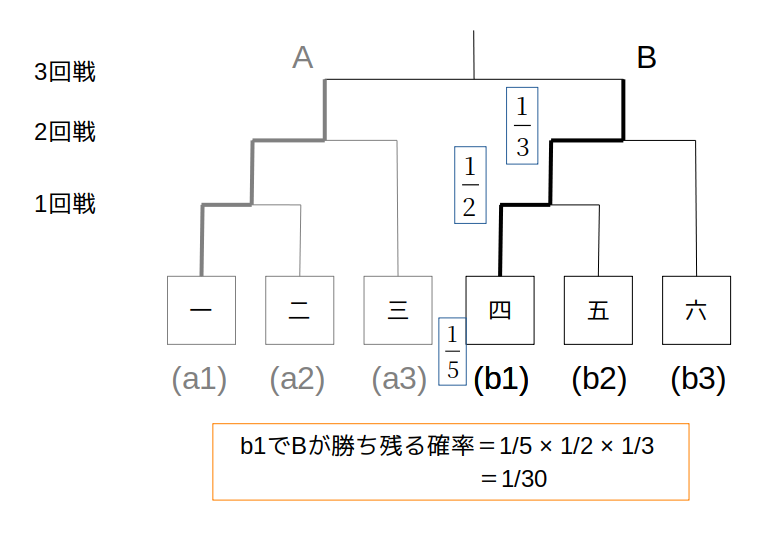
くじ引きでBが「四」になる確率は\(\frac{1}{5}\)
このときにBが3回戦に進む確率は、
なので、
\(\frac{1}{2}×\frac{1}{3}=\frac{1}{6}\)
よって、B=b1で勝ち残る確率は、
\[
\frac{1}{5}×\frac{1}{6}=\frac{1}{30}
\]
(b2)Bが3回戦まで勝つ確率→\(\frac{1}{30}\)
(b1)と全く同じ。
(b2)で(A,B)となる確率は、\(\frac{1}{30}\)
(b3)Bが3回戦まで勝つ確率→\(\frac{2}{15}\)
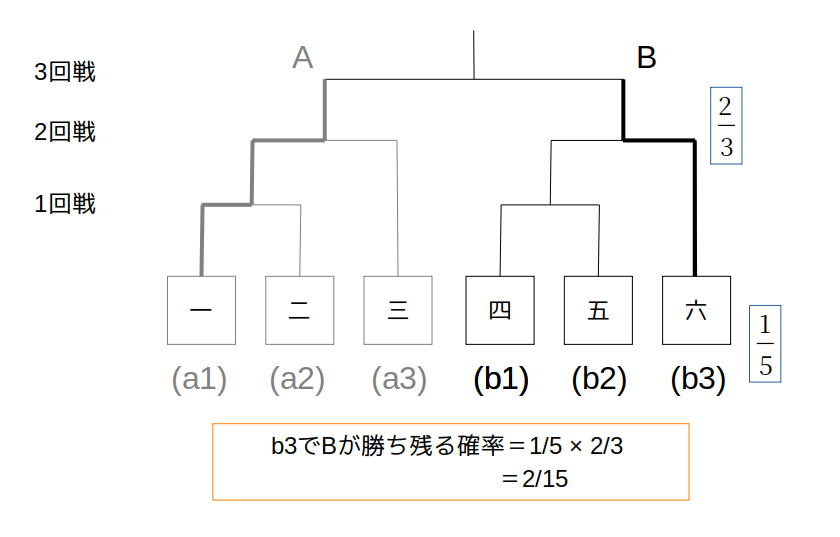
くじ引きでBが「六」になる確率は\(\frac{1}{5}\)
1回戦目は、どちらが勝ってもOK(確率\(1\))
2回戦目でBが勝つ(確率\(\frac{2}{3}\))のであれば、
\(1×\frac{2}{3}=\frac{2}{3}\)
B=b3で勝ち残る確率は、
\[
\frac{1}{5}×\frac{2}{3}=\frac{2}{15}
\]
Bが勝つ確率:排反事象の足し算
b1〜b3は、いずれも同時に起こらない(排反)ので、Bが勝つ確率は、
\[
\frac{1}{30}+\frac{1}{30}+\frac{2}{15}=\frac{1}{5}
\]
(A,B)の確率→\(\frac{1}{180}\):独立事象のかけ算
各試合は互いに影響し合わない(独立)ので、
a1で(A,B)となる確率は、
\[
\mathrm{a1}:\frac{1}{36}×\frac{1}{5}=\frac{1}{180}
\]
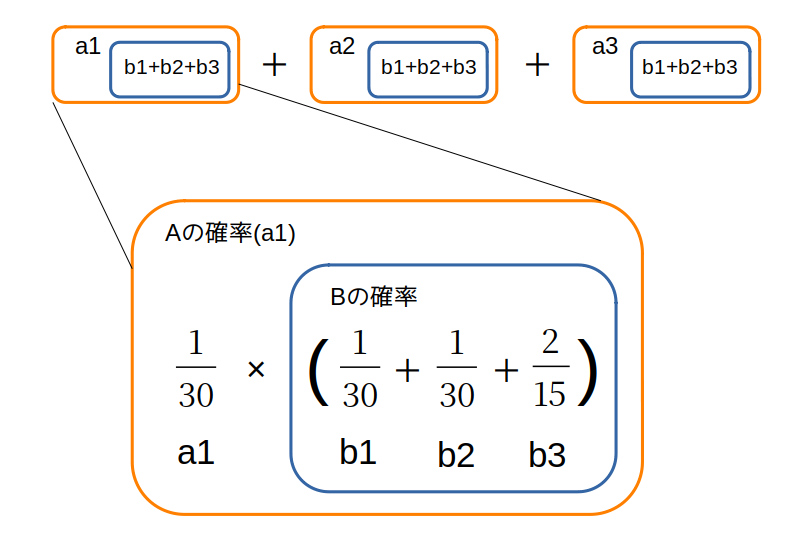

a2とa3も、同じように求められる
a2とa3も、同じように求められます。
(a2)(A,B)の確率→\(\frac{1}{180}\):a1と同じ
(a1)と、状況は全く同じ。
→a2で(A,B)となる確率は、\(\frac{1}{180}\)
(a3)Aが3回戦まで勝つ確率→\(\frac{1}{9}\)
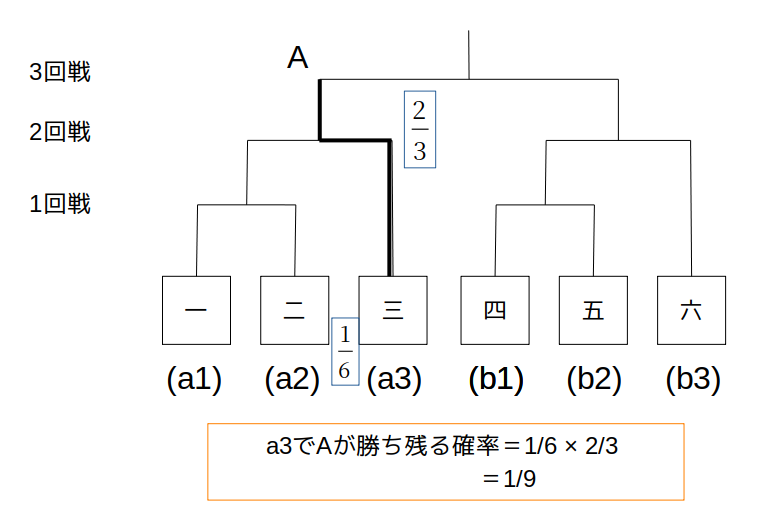
くじ引きでAが「三」になる確率は\(\frac{1}{6}\)
このとき、Aが勝つ確率は、
なので、
\(1×\frac{2}{3}=\frac{2}{3}\)
よって、A=a3で勝ち残る確率は、
\[
\frac{1}{6}×\frac{2}{3}=\frac{1}{9}
\]
b1〜b3は同じ→Bの確率=\(\frac{1}{5}\)
次は、b1〜b3それぞれでBが勝つ確率。
といっても、B側はa1の場合と全く同じ。
(b1, b2, b3)=(\(\frac{1}{30}, \frac{1}{30}, \frac{2}{15}\))
→Bが勝つ確率:\(\frac{1}{5}\)
a3で(A,B)となる確率は、
\[
\mathrm{a3}:\frac{1}{9}×\frac{1}{5}=\frac{1}{45}
\]
(A,B)の確率:a1〜a3は排反
(A,B)の確率=a1+a2+a3、であったことを思い出せば、
\[
\frac{1}{180}+\frac{1}{180}+\frac{1}{45}=\frac{1}{30}
\]
ここに、×(パターン数)で求める確率になります。
あともう一息。
(□, □)のパターン数=A〜Fから2個取る順列
ここまで、3回戦のペアを(A,B)に固定して考えてきました。
実際には、ペアの数だけ確率\(\frac{1}{30}\)があります。

(A,C)も、(B,F)も、すべて確率\(\frac{1}{30}\)
しかも、どのペアも同時に起こらない(排反)ので、条件に合うペアの数だけ\(\frac{1}{30}\)を足し合わせれば、求める確率になります。
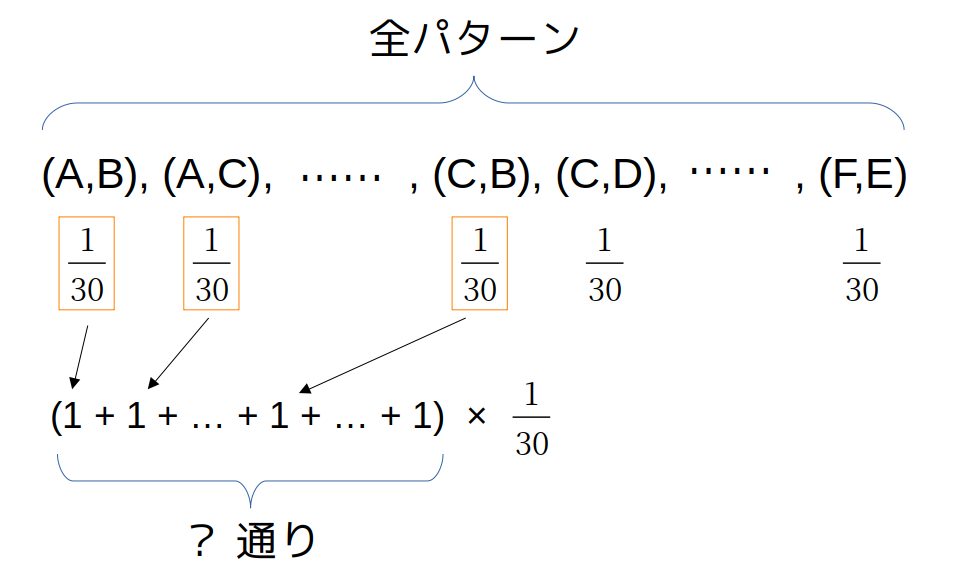
条件を満たすペアはいくつでしょう?
A〜Fの中から2つ選んで、3回戦のポスト(□,□)に当てはめる、と考えれば、順列が使えます。
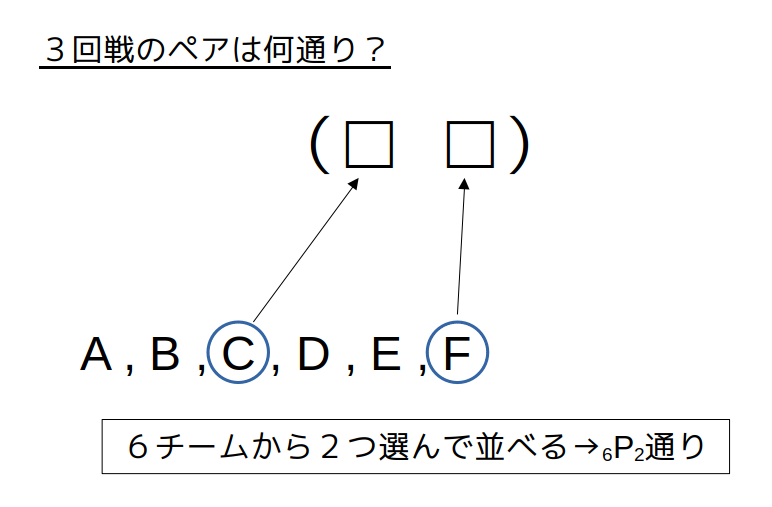

(A,B)と(B,A)を別物と考えるなら順列
全パターン:\({}_6 \mathrm{P}_2=6×5=30\)通り
AもBも含まれない:\({}_4 \mathrm{P}_2=4×3=12\)通り
→AまたはBを含む:\(30-12=18\)通り
AまたはBが3回戦に進む確率は、
\[
18×\frac{1}{30}=\frac{3}{5}
\]
よって、3が正解です。

樹形図で数えてもOK
別解:定義からも確率を求められる
勝ち負けの確率を使わず、定義から求める方法もあります。
3回戦に上がってくるのは誰か、という点で考えれば、起こりうる全てのパターンは\({}_6 \mathrm{C}_2=15\)通りに言い尽くされています。
このうち、AもBもいないパターンは\({}_4 \mathrm{C}_2=6\)通り
→AまたはBがいるパターンは15ー6=9通り
→\(\frac{9}{15}=\frac{3}{5}\)と求めることもできます。
おわりに:「数え上げて定義」か「確率から確率」か
お疲れ様でした!
確率(&場合の数)を解くための道具は5つ。
数え上げ、順列&組み合わせ、和の法則、積の法則、余事象です。
場合分けの先で場合分けが必要になる、確率の問題でした。
場合分けの入れ子構造を念頭に置きつつ、自分がいまどのケースを扱っているのか、迷わないように進めましょう。

数え忘れたり、同じものを数えないように気をつけよう
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!次回もお楽しみに!
次回もお楽しみに!
略解
3回戦のペアが(A,B)となる確率を考える。
次図のように、AとBの位置によって場合分けする。

(A,B)→別々のブロックに振り分けられる
(a1)Aが「一」の場合
Aが勝ち残る確率は、1回戦も2回戦も勝つ確率なので、
\[
\frac{1}{6}×\frac{1}{6}=\frac{1}{36}
\]
(b1)Bが「四」の場合
くじ引きでBが「四」になる確率は\(\frac{1}{5}\)
Bが勝ち残る確率は、1回戦も2回戦も勝つ確率なので、
\[
\frac{1}{5}×\frac{1}{6}=\frac{1}{30}
\]
(b2)Bが「五」の場合
同じく、
\[
\frac{1}{5}×\frac{1}{6}=\frac{1}{30}
\]
(b3)Bが「六」の場合
Bが「六」になる確率は\(\frac{1}{5}\)
Bが勝ち残る確率は、2回戦で勝つ確率なので、
\[
\frac{1}{5}×\frac{2}{3}=\frac{2}{15}
\]
b1〜b3は排反なので、Bが勝つ確率は、
\[
\frac{1}{30}+\frac{1}{30}+\frac{2}{15}=\frac{1}{5}
\]
AとBの試合は互いに独立なので、
a1で(A,B)となる確率は、
\[
\mathrm{a1}:\frac{1}{36}×\frac{1}{5}=\frac{1}{180}
\]
(a2)Aが「二」の場合
(a1)と同じく、(A,B)となる確率は、\(\frac{1}{180}\)
(a3)Aが「三」の場合
Aが「三」になる確率は\(\frac{1}{6}\)
Aが勝ち残る確率は、2回戦で勝つ確率なので、
\[
\frac{1}{6}×\frac{2}{3}=\frac{1}{9}
\]
b1〜b3についてはa1の場合と全く同じ。
→Bが勝つ確率:\(\frac{1}{5}\)
a3で(A,B)となる確率は、
\[
\mathrm{a3}:\frac{1}{9}×\frac{1}{5}=\frac{1}{45}
\]
a1〜a3は互いに排反なので、(A,B)の確率は
\[
\frac{1}{180}+\frac{1}{180}+\frac{1}{45}=\frac{1}{30}
\]
3回戦のペアについて、
全パターン:\({}_6 \mathrm{P}_2=6×5=30\)通り
AもBも含まれない:\({}_4 \mathrm{P}_2=4×3=12\)通り
→AまたはBを含む:\(30-12=18\)通り
AまたはBが3回戦に進む確率は、
\[
18×\frac{1}{30}=\frac{3}{5}
\]
したがって、3が正解である。





コメント
演習問題の「トーナメントの決勝戦に勝ち残る確率」の解答において、(i-d)(iii-a)のケースなどで、Bを配置する確率(1/5や2/5など)を掛けるのを忘れていると思います。
この問題の場合、AからFのチームは全て対等なので、3回戦で戦うチームの組合せは
(A,B),(A,C),…,(E,F)の6*5/2=15通りで、これらは同様に確からしく、
このうちAまたはBが決勝戦で残らない4*3/2=6通りが余事象にあたるので、1-6/15=3/5が正しいのではないでしょうか。
>(i-d)(iii-a)のケースなどで、Bを配置する確率(1/5や2/5など)を掛けるのを忘れていると思います。
見直したところ、見事に計算間違いをしておりました
墓場まで持っていく秘密がまた一つ増えたようです
>この問題の場合、〜
改めて解き直したところ、確率3/5でした
3回戦のペアはどうあがいても(A,B),(A,C),…,(E,F)の6*5/2=15通りにしかなり得ないから、これを全事象としてしまおう、という考え方ですね
これは一〜六が対等だから成せる技で、もし「不均一なサイコロで場所を決める」という条件だったら、同様に確からしくないので地道な場合分けが必要になりますね
よく勉強してらっしゃるんだな、と感心いたしました
今後とも本サイトをよろしくお願いします