こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、半角丸長方形を積み重ねる問題をやりましたね。
平面図形に、規則性の要素をからめた複合問題です。
まだ問題を見てない方はぜひ挑戦してみてください。
解き終わった方も、復習は大切です。
それぞれの解法は隅々まで理解してこそ、本番で活用することができるものです。
「分かったつもり」のままだと、初見で似たような問題を見ても正答は覚束ないでしょう。
問題演習では、数をこなすのももちろん重要ですが、解いた問題の一つ一つを確実に習得することも忘れてはなりません。
昨日解いた問題に似た問題が出題されたとしたら、自信を持って解答できますか?
少しでも不安のある方は、再度同じ問題にトライしてみることをおすすめしますよ。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
ある企業16社に対し、ある年の新入社員の人数を調べたところ、統計上の数値は下表の通りであった。この表に関連する用語として、平均値と標準偏差、および中央値の定義を以下に示す。
| 社数 | 16社 |
| 平均値 | 4人 |
| 中央値 | 0人 |
| 最大値 | 48人 |
| 最小値 | 0人 |
| 標準偏差 | 12人 |
平均値:\(M=\frac{x_1+x_2+…+x_N}{N}\)
標準偏差:\(S=\sqrt{\frac{(x_1-M)^2+(x_2-M)^2+…+(x_N-M)^2}{N}}\)
中央値:データを大きさの順に並べたとき、ちょうど中央に位置する値。
\(N\)が奇数→\(\frac{N+1}{2}\)番目の値
\(N\)が偶数→\(\frac{N}{2}\)番目の値と\(\frac{N}{2}+1\)番目の値の平均値
このとき、確実に正しいといえる記述は次のうちどれか。
- 新入社員の人数が2人以上いる会社は、ちょうど4社である。
- 新入社員の人数が2人以上いる会社は、ちょうど6社である。
- 新入社員の人数が2人以上いる会社は、ちょうど5社である。
- 新入社員の人数が2人以上いる会社は、ちょうど9社である。
- 新入社員の人数が2人以上いる会社は、ちょうど2社である。
5
統計上の数値を扱う問題です。
数学が苦手な方も、落ち着いて、まずは条件からいえることはないか、考えてみましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
問題文の表現によると、標本数\(N=16\)、平均値\(M=4\)、標準偏差\(S=12\)ですね。
また、対象の16社を新入社員の人数によって大きい方から順に並べたとき、\(n\)番目の会社の新入社員の人数を\(x_n\)としますと、\(x_1=48\)です。
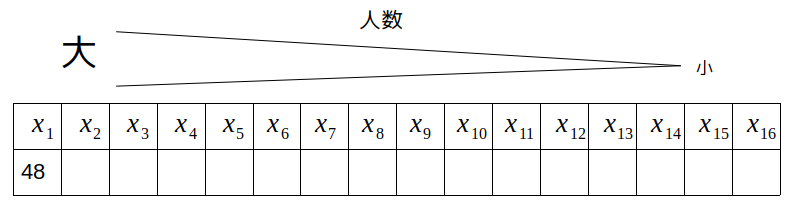
まず注目すべきは、「中央値が0」という事実です。
今回は\(N\)が偶数なので、問題文の「定義」によると、中央値は\(\frac{x_8+x_9}{2}\)です。
これが0なので、\(x_8=x_9=x_{10}=…=x_{16}=0\)となります。

ここからは標準偏差に注目します。
表の値を、「定義」の式に代入してみましょう。
\[
S=12=\sqrt{\frac{(48-4)^2+(x_2-M)^2+…+(x_7-4)^2+(0-4)^2+…+(0-4)^2}{16}}
\]
整理すると、\((x_2-4)^2+(x_3-4)^2+…+(x_7-4)^2=224\)……(※)
ここで、\(4×16-48=16\)なので、\(x_2〜x_7\)の合計は\(16\)でなければなりません。
これに基づいて、例えば\(x_2=11, x_3=x_4=…=x_7=1\)とすると、
\((※の左辺)=7^2+3^2×5=94\)となり、右辺に届きません。
代わりに\(x_2=12, x_3=x_4=…=x_6=1, x_7=0\)としてみると、
\((※の左辺)=8^2+3^2×4+4^2=116\)
ちょっと近づきましたが、まだ右辺の値には届きませんね。
このように、0の数を増やすと(※の左辺)は増加します。
ならば、いっそ\(x_2=16, x_3=x_4=…=x_7=0\)としてみたらどうでしょう?(これが最大)
\((※の左辺)=12^2+4^2×5=224=(右辺)\)となり、辻褄が合います。
あまりにも場当たり的な解法なので、
「他にも辻褄の合う値の組があるのでは?」
と思われる方もいるでしょう。
しかし、(※の左辺)が取れる値としては、上述したケースが唯一にして最大です。
手がかりとなるのは、「関数\(y=(x-4)^2\)の増減」と「\(x_2〜x_7\)の合計は\(16\)」という条件です。
前者について、\(x=0\)から始まって\(1\)ずつ増えていくとき、\(y\)は始めのうちは減少し\(x=4\)で最小値をとります。
そこからは増加に転じますが、\(x=8\)でやっとスタートライン(\(x=0\)と同じ値)に戻ってきます。
つまり、\(x_n\)の値をいくら増やそうが、それが\(0≦x≦8\)の間である限り、(※)の左辺は\(224\)より大きくなりようがないのです。
「だったら\(x_n\)を\(9\)以上に増やしてやればいいのでは?」
と思われるかもしれませんが、「\(x_2〜x_7\)の合計は\(16\)」という拘束条件があるので、増やすにも限界があります。
この条件のおかげで、例えば\(x_2=9\)としたところで、たかだか\(x_3=7\)(他は全て0)にしかならず、結果として(※)の右辺は\(224\)より小さくなってしまいます。
結局、(※)の右辺を\(224\)まで持っていくには、最大の値である\(x_2\)にリソース(=\(16\))を極振りして、他を0としてしまうほかないのです。
以上をまとめると、\(x_1=48, x_2=16, x_3=x_4=…=x_16=0\)となります。
よって、5が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
ささやかながら骨のある統計の問題でした。
用語の定義を始めとする必要な知識は与えられているものの、統計分野に免疫のない方にはなかなか難しい問題だったのでは、と思います。
何しろ過去には前例の少ないタイプの問題なので、傾向を分析して真面目に数的処理の対策をされてきた方は少々面食らったかもしれません。
本問のようにマトモな統計の問題は、私の知る限りでは他に出題例がないので、話半分に解説を理解するだけでも十分でしょう。
もし本番で見かけていたら、私ならひとまずスルーすると思います笑
いずれにせよ、本番まであまり時間のない方は、対応関係とか、図形問題とかを優先して対策する方が賢明でしょう。
時間が限られている方には、出題傾向によって緩急をつけた学習もおすすめです。
(さて、この問題のカテゴリ分けどうしようかな……)
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!次回もお楽しみに!
次回もお楽しみに!
略解
問題文より、標本数\(N=16\)、平均値\(M=4\)、標準偏差\(S=12\)
また、対象の16社を新入社員の人数によって大きい方から順に並べたとき、\(x_1=48\)
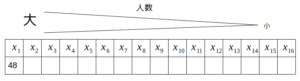
標本を大きい順に並べる
「中央値が0」であり、中央値が\(\frac{x_8+x_9}{2}\)であることより、
\(x_8=x_9=x_{10}=…=x_{16}=0\)

「中央値が0」から分かること
ここで、標準偏差について、
\[
S=12=\sqrt{\frac{(48-4)^2+(x_2-M)^2+…+(x_7-4)^2+(0-4)^2+…+(0-4)^2}{16}}
\]
すなわち、\((x_2-4)^2+(x_3-4)^2+…+(x_7-4)^2=224\)
\(4×16-48=16\)より、\(x_2〜x_7\)の合計は\(16\)である。
これに基づき、例えば\(x_2=11, x_3=x_4=…=x_7=1\)とすると、
\((※の左辺)=7^2+3^2×5=94\)となり、右辺に届かない。
次に、\(x_2=12, x_3=x_4=…=x_6=1, x_7=0\)としてみると、
\((※の左辺)=8^2+3^2×4+4^2=116\)となり、まだ右辺の値には届かない。
同様に、0の個数を1つずつ増やしていき、※の左辺を調べると、
\(x_2=16, x_3=x_4=…=x_7=0\)のとき、
\((※の左辺)=12^2+4^2×5=224=(右辺)\)となり、辻褄が合う。
よって、\(x_1=48, x_2=16, x_3=x_4=…=x_16=0\)
したがって、5が正解である。


コメント