こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
朝、お風呂に入ってから会社に行くと、一日とてもいい気分。
前回は、部内会議が行われた時間帯を明らかにする問題でした。
知りたい情報を可視化する方法のバリエーションを増やしましょう。
ぜひ解いてみてください。
もう解いた方は、お疲れ様でした。
新しい問題に挑戦するのと同じくらい大切なのが「復習」です。
ぜひ取り入れてほしいオススメのやり方として、「解法の一般化」というのがあります。
個々の問題の解説から、似た問題に活用できる手法を抽出し、身に付けるのです。
数的処理は、解説そのものを丸暗記してもあまり上達しません。
過去問と全く同じ問題が出る可能性は限りなくゼロに近いからです。
積極的に解説に向き合って、ホンモノの対応力を磨きましょう!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
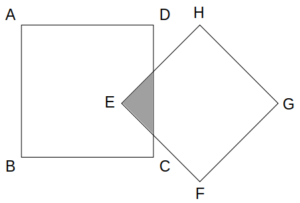
同一平面上にある合同な2つの正方形ABCDとEFGHがある。いま、これら正方形が交わるときに辺の成す角が45°となるように回転させた状態から始めて、平行移動のみにより共通領域の面積を最大化することを考える。このとき、共通領域の最大値は正方形ABCDの何倍か。
- \(2(\sqrt{2}-1)\)倍
- \(2(3\sqrt{2}-4)\)倍
- \(\frac{3(4\sqrt{2}-5)}{2}\)倍
- \(4(8\sqrt{2}-11)\)倍
- \(\frac{10\sqrt{2}-13}{2}\)倍
1
正方形とひし形の共通領域の問題です。
面積の問題といえば、対処法は2つですね。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
面積について議論する前に、共通領域が最大となるのはどんな場合かハッキリさせましょう。
形も何も分からない状態では、面積を求めることもできませんからね。
結論を言いますと、次図のように、2つの正方形の中心が一致するときに最大となります。
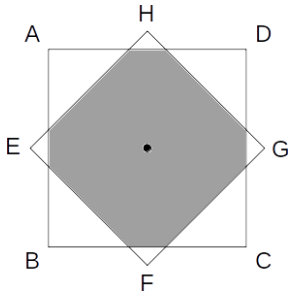
理屈がほしい方は、正方形EFGH(ひし形)を左右にちょっとだけスライドさせてみると分かります。
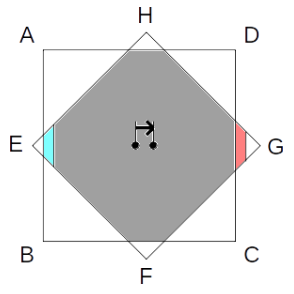
試しにひし形を右に少しスライドさせると、図の青い領域がプラスされる代わり、赤い領域がマイナスされます。
大きさは「青<赤」なので、全体の収支はマイナスです。
つまり、スライドさせる前(=中心が一致した状態)の方が共通領域の面積は大きかった、ということです。
ひし形を左に、あるいは上下にスライドさせた場合にも全く同じことがいえるので、共通領域は「中心が一致した状態」に最大となることが示されます。
形が決まったら、あとは面積を具体的に求めるだけです。
面積の問題の考え方は2つありましたね。
- 大きさが分かっている図形との比から求める方法
- 具体的に長さを求めて面積公式に当てはめる方法
今回は「共通領域の最大値は正方形ABCDの何倍か」を聞かれているので1、かと思いきや、2の方針が有効です。
基準は正方形ABCDの面積なので、1辺の長さを1とすると分かりやすくなります。
対称性を考えて、図形を四分割します。
次図の赤い領域に注目です。
これは直角三角形で、線分OHから図の赤線を引くことにより高さを求められます。
\(\mathrm{OH}-(赤線)=\frac{\sqrt{2}-1}{2}\)
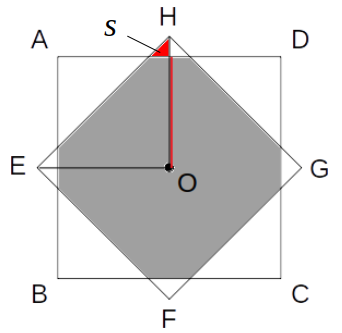
赤い三角形(面積を\(s\)とします)は△OEHと相似の関係にあり、相似比は\(\frac{\sqrt{2}-1}{2}:\frac{\sqrt{2}}{2}\)
面積比は、
\begin{eqnarray}
s:△\mathrm{OEH}&=&\left(\frac{\sqrt{2}-1}{2}\right)^2:\left(\frac{\sqrt{2}}{2}\right)^2 \\
&=&\frac{3-2\sqrt{2}}{4}:\frac{1}{2} \\
&=&\frac{3-2\sqrt{2}}{2}:1
\end{eqnarray}
これは、赤い三角形の面積が△OEHの\(\frac{3-2\sqrt{2}}{2}\)倍であることを表しています。
正方形ABCDの面積は△OEHを4倍したものなので、\(s\)とは次のような関係があります。
\begin{eqnarray}
4s:\mathrm{ABCD}&=&2(3-2\sqrt{2}):4 \\
&=&\frac{3-2\sqrt{2}}{2}:1
\end{eqnarray}
これは、赤い正方形4つ分の面積が正方形ABCDの\(\frac{3-2\sqrt{2}}{2}\)倍であることを示します。
対称性より、赤い三角形は全体に8つあります。
求める共通領域の面積は、ひし形(=正方形)から赤い三角形8つ分(=\(4s\)の2倍)を除くことで得られ、
\[
1-\frac{3-2\sqrt{2}}{2}×2=2(\sqrt{2}-1)
\]
これが求める答えです。
よって、1が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
正方形とひし形の共通領域を最大化して面積を求める問題でした。
初手として、領域が最大となるのはどんな場合か、形を明らかにすることが必要です。
解説では、最大である理由についても議論しましたが、本番なら「なんとなくこれっぽい」と思ったら決めつけて進めてOKです。
進めてみて得られた答えが、選択肢の中にあればシメたもの。
それを選んで次の問題に進みましょう。
数的処理は選択式の試験なので、途中の議論はある程度大づかみに進めても大丈夫です。
少しくらい大ざっぱな考察から得られた解答ならば、勘だけを頼りに選んだ解答よりも断然信ぴょう性があると考えましょう。
後半の面積を求める段階では、「解法のポイント」が使えます。
「この記事で初めて知った」という方は、ぜひ頭に入れて活用してください。
問題の文言に惑わされることなく、適切な方針を選択できるように練習しましょう。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
共通領域が最大となるのは、次図のように、2つの正方形の中心が一致するときである。
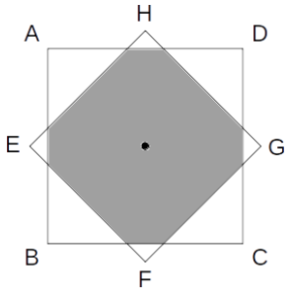
共通領域が最大となるとき
以下では、正方形ABCDの1辺の長さを1とし、対称的な4つの領域に分割して考える。
次図の赤い領域(直角三角形)の高さは、線分OHから図の赤線を引くことにより求められる。
\(\mathrm{OH}-(赤線)=\frac{\sqrt{2}-1}{2}\)
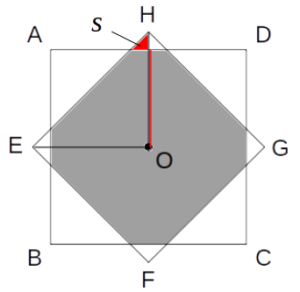
はみ出た領域の面積を求める
赤い三角形(面積\(s\))と△OEHは相似であり、相似比は\(\frac{\sqrt{2}-1}{2}:\frac{\sqrt{2}}{2}\)
これより、面積比は
\begin{eqnarray}
s:△\mathrm{OEH}&=&\left(\frac{\sqrt{2}-1}{2}\right)^2:\left(\frac{\sqrt{2}}{2}\right)^2 \\
&=&\frac{3-2\sqrt{2}}{4}:\frac{1}{2} \\
&=&\frac{3-2\sqrt{2}}{2}:1
\end{eqnarray}
正方形ABCDの面積は△OEHを4倍したものであることから、\(s\)とは次のような関係がある。
\begin{eqnarray}
4s:\mathrm{ABCD}&=&2(3-2\sqrt{2}):4 \\
&=&\frac{3-2\sqrt{2}}{2}:1
\end{eqnarray}
対称性を考えると、赤い三角形は全体に8つあるから、求める共通領域の面積は、ひし形(=正方形)から赤い三角形8つ分(=\(4s×2\))を除いたもので、
\[
1-\frac{3-2\sqrt{2}}{2}×2=2(\sqrt{2}-1)
\]
したがって、4が正解である。

コメント
解説文の「これは、赤い三角形の面積が正方形の」の部分は「これは、赤い三角形の面積が正方形の1/4の」とするのが正しいので、赤い三角形8つ分の面積は 3-2√2 になり、答えは 2√2-2倍 になります。
8√2-11≒0.31 なので、明らかに1/2以上になるはずの本来の答えとは異なる事がわかります。
コメントありがとうございます。
サイトをご活用いただけており嬉しく思います。
ご指摘の通り、最初の面積比は正方形ではなく△OEMとの関係を示したはずのものでした。
このことを明確にするため、△OEMとの比を正方形との比に読み替えるプロセスを追記しました。
解答も、2(√2-1)倍が正解となります。
「8√2-11≒0.31 なので、明らかに1/2以上」という部分、考えてみれば明らかにおかしいと分かりますね…
今後とも本サイトをどうぞよろしくお願いします!