大型連休が可能な年

こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます！
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
模擬テストのアクセス数が思ったより少なくても、めげない、心折れない。

前回は、10枚のカードの並べ替え操作を繰り返す問題をやりましたね。
まだ見てない方はぜひチャレンジしてみてください。
もう解いたよーという方は、復習を忘れずに。
質より量を重視した問題演習も悪くはないですが、せめて一度解いた問題の解答は自力で導けることを確かめてから次に進んでいってほしいと思うんです。
一度解いた問題が解けないようでは、たとえ本番で似たような問題を見ても取りこぼしてしまう可能性が高いですよね。
せっかく勉強しているのに、もったいない話です。
ならどうすればいいか、ですが、おすすめの勉強法は「解き直し」です。
解き直しをすると、思わぬポイントでつまずいて解ききれない、ということが多々あるかと思いますが、問題ありません。
次はつまずかないように、もう一度納得するまで解説をよく読んでみてください。
乗り越えた先には、解法に対する一段と深い理解があります。
そうして何度も解き直しをしていく中で、一つの解法を研究し尽くすことができれば、少しひねった初見の問題にも対処できます。
本番では必ず初見の問題を解かなければならないからこそ、解き直しにより解法に対する理解を深めておく必要があるのです。
ぜひ、解き直しを普段の勉強に取り入れてみてください。

復習がバッチリな方は、本日の問題へ参りましょう！

本日の演習問題

カレンダー通りに休日がある会社で、9日以上の連休になる年を数える問題です。
年ごとの休日の配置を調べる必要がありそうですね。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。

それではスタート！

詳しい解説

4/29〜5/8における曜日の並びは、「5/1が何曜日か」という点に注目すれば、たかだか7通りしかないことが分かります。
そこで、先にこの7通りを全て列挙してしまった後で、2022年〜2050年の各年がそれぞれどの並びに該当するのかを考え、年ごとの休日の配置を明らかにします。

まず、曜日の並びを7通り全て書き出してみます。

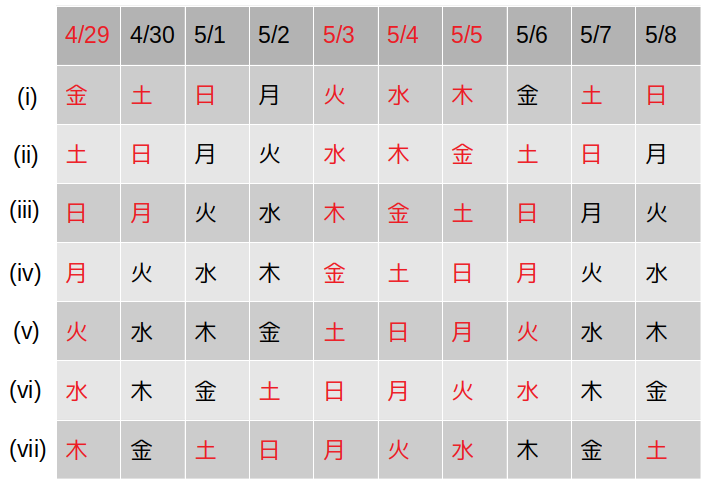
赤字は休日を表します。
これを見ると、(i)は5/2と5/6で休暇を取得すれば10連休となります。
また(ii)も、5/1と5/2で休暇を取得すれば9連休となることが分かります。
結局、本問の主旨は(i)または(ii)に該当する年を明らかにすることである、と言えますね。

あとは、2022年〜2050年の各年を上図の(i)〜(vii)のうちの該当するパターンに振り分けていきます。

まず「年数が4の倍数」ではない年について、365÷7＝52…1より、年数が1増えるごとに曜日は一つずつズレていくことが分かります。
例えば、ある年の5/1が日曜日だったら、次の年の5/1は月曜日、という具合にスライドしていきます。

同じように「年数が4の倍数」の年について考えると、366÷7＝52…2より、4の倍数の年の翌年は曜日が二つズレることが分かります。
（4の倍数のある年の5/1が日曜日なら、その翌年の5/1は火曜日です）

以上の規則に従うと、まず2022年の5/1は日曜日なので(i)です。
翌年、2023年の5/1は月曜日なので(ii)ですね。
さらに翌年の2024年（4の倍数！）の5/1は火曜日で(iii)です。
さらにさらに翌年の2025年の5/1は水曜日、ではなく木曜日で(v)です。

同様にして2050年までの各年を振り分けていくと、次のようになります。

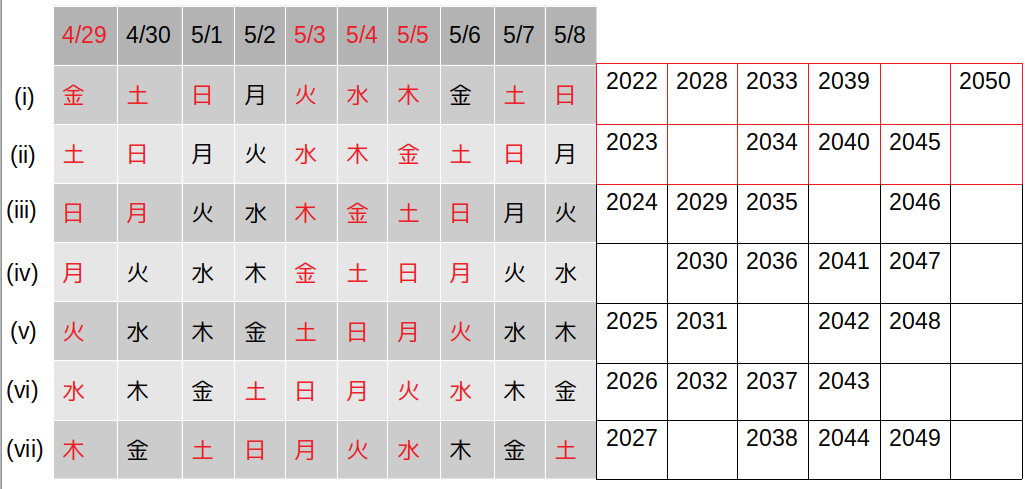
題意に該当するのは図の赤枠に含まれる年で、全部で9つあることが分かります。

よって、４が正解です。

おわりに

お疲れ様でした！
いかがだったでしょうか？

GWに大型連休が実現できる年を探すという、実生活に応用したくもなる面白い問題でしたね。
（私も今年のGWは10連休にしようかな……）
解法としては、曜日の並びが7パターンしかないことに気づいて、書き出してみることが第一歩です。
曜日が年ごとに一つずつズレるのは常識として知っているのが好ましいですが、理屈で説明すると解説のようになります。
あとはうるう年に気をつけつつ、各年が7パターンのどれに該当するか、丁寧に調べましょう。
なお、うるう年の定義は「4の倍数」という条件にいくつかの例外が加わります。
本問を解く上では必要のない知識ですが、常識として知っておくとどこかで役に立つ（？）かもしれません。
強引に公務員試験と結びつけるなら、時事問題のネタになりそうなくらい（適当ですが……）

本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします！

次回もお楽しみに！

略解