こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、アルファベットのカードを配布するうそつき問題でした。
実戦レベルでありながら、うそつき問題の基本的なアプローチを学べる問題です。
一見複雑な問題であっても、基本に忠実になれば解決できるという教訓が得られる内容になっています。
解いてない方はぜひチャレンジしてみてください。
今回のテーマは「対応関係」です。
対応関係で最初に必ずしなきゃいけないことがあるんですが、知ってますか?
知らない方は、以下の記事がオススメです。

最初にすべきことが分かると、初見の問題も解きやすいよ
演習問題:くじ引きの合計得点
A〜Fの6人でくじ引きを3回行い、引いたくじに書かれた数字の合計が大きい者から順位を付けた。
参加者はa、b、cの3つの箱から1回ずつ、計3回くじを引き、直ちに数字をメモし引いたくじを元の箱に戻した。箱の中身は、それぞれ次のようであったとする。
◎ a:1〜4のうちのいずれか異なる数字が書かれた3本のくじ(数字の小さいものから順にア、イ、ウとする)
◎ b:1〜3のうちのいずれか異なる数字が書かれた3本のくじ(数字の小さいものから順にエ、オ、カとする)
◎ c:1〜3のうちのいずれか異なる数字が書かれた2本のくじ(数字の小さいものから順にキ、クとする)
くじ引きについて、次のことが分かっているとき、確実に正しいといえる記述はどれか。
- ア、イ、ウを引いた者の人数は、それぞれ2人ずつであった。
- エ、オ、カを引いた者の人数は、それぞれ2人ずつであった。
- キ、クを引いた者の人数は、それぞれ3人ずつであった。
- aについて、AとFはイを引き、CとEはウを引いた。
- bについて、AとDはオを引き、BとCはエを引いた。
- アとウの数字の差は2であった。
- 各自がaとbから引いたくじの数字の和は、Cが5、Eが7、Fが6であった。
- cから引いたくじが一致した3人は、aとbからは異なるくじを引いた。
- BとCの順位は同じであった。
- Aは1位であった。
- Bが引いたくじに書かれた数字の合計は6で、3位であった。
- Dが引いた3つのくじに書かれた数字は全て2であった。
- キとクに書かれた数字の合計は5であった。
- Eが引いたくじに書かれた数字の合計は10であった。
5
くじ引きの合計点を競う問題です。
条件の数は多いですが、基本に忠実に、分かることを整理するところから始めましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
対応関係は「表」から始まります。
まずは適切なフォーマットを用意すること
- 項目が2つ→○×式
- 項目が3つ→数字など書き込み式
必要となる情報は、
本問では、「ア〜クに書かれた数字」と、それを誰が引いたのか、つまり「人(A〜F)」の2つです。
これらが分かれば、最終的な順位付けや合計数に関する選択肢の正誤が分かりますね。

表現したい要素が2つだから、○×式の表にしよう
次のような表を用意します。

誰がどのくじを引いたのか?
各くじの人数に関する条件ア、イ、ウを引いた者の人数は、それぞれ2人ずつであった。
エ、オ、カを引いた者の人数は、それぞれ2人ずつであった。
キ、クを引いた者の人数は、それぞれ3人ずつであった。
を前提に、各くじを引いたのが誰なのかを明らかにしましょう。
また、 bについての条件bについて、AとDはオを引き、BとCはエを引いた。 より、EとFはカを引いたことになります。

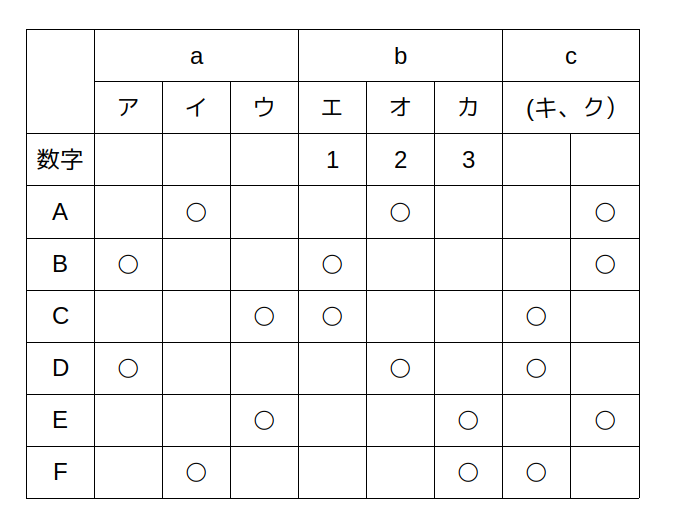
ここまでを表に記入しよう

cについては、
最後から2番目の条件cから引いたくじが一致した3人は、aとbからは異なるくじを引いた。
を使います。
表を見て、aでもbでも引いたくじが被らないような3人を選び出すと、AとBとEが該当します。
これより、AとBとEはキとクの一方を引いて、CとDとFはもう一方を引いたことが分かるので、これを記入します。

2つのグループがそれぞれキとクのどちらを引いたのかはまだ確定できない
平面図形の面積を徹底攻略シリーズ!第1回!(全2回)
\\\【図形の折り返しと面積】///
図形の面積を求める問題って、実は大まかに2つのパターンしかないのをご存知ですか?
ここではそのうちの一つ、公式を利用するパターンの解法が紹介されています。
これを読めば、面積の問題の半分は攻略できたも同然!?
ぜひチャレンジしてみてください。
Twitterもよろしくね!↓
ア〜クはそれぞれ何点か?
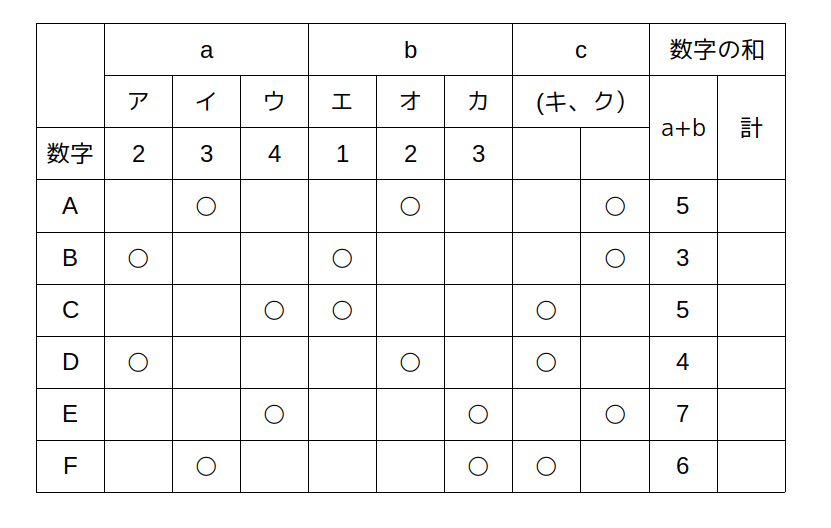
aとbから引いたくじの和に関する条件各自がaとbから引いたくじの数字の和は、Cが5、Eが7、Fが6であった。
と作った表を合わせて考えると、Eはbで3を引いているので、aでは4を引いたことになります。
Eがaで引いたのはウなので、ウは4と決まります。
このことは、Cのa+bが5であることにも矛盾しません。
このことと、 アとウの差に関する条件アとウの数字の差は2であった。 より、アは2と決まります。
これとFのa+bが6であること、Fがbで3を引いていることより、Fはaでは3(=イ)を引いたことになります。
ここまでを表にすると以下のようになります。
分かりやすいように、表には「a+b」と「合計点」の項目を追記してあります。

実際の試験だったら表の横にメモ程度に付け足せばOK
この表と、
BとCの順位に関する条件BとCの順位は同じであった。
を使うと、キとクの数字も分かります。
Bの「3」とCの「5」に何かを加えて同順位(=同じ数)にするには、キが1、クが3であればいいですね。
このことを含め、最終的な結果を表に記入すると、次のようになります。
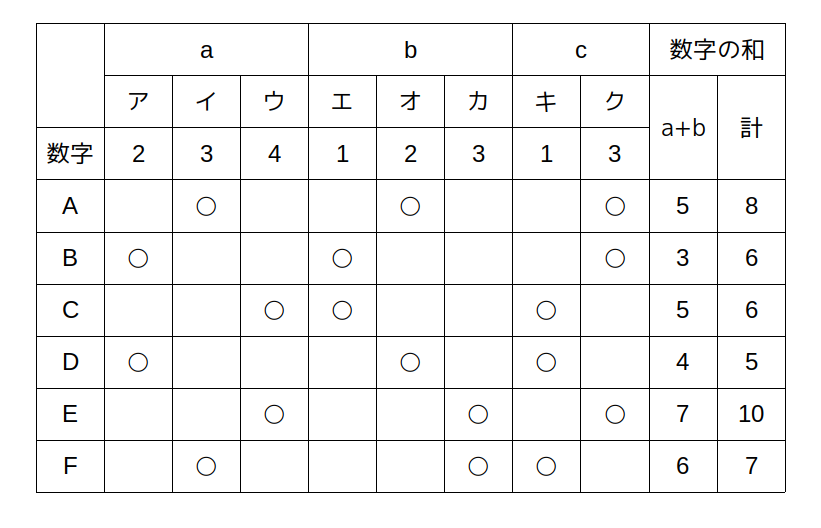
この表をもとに選択肢を検討すると、正しい記述は5しかありません。
よって、5が正解です。
おわりに:対応関係は表がなければ始まらない
お疲れ様でした!
いかがだったでしょうか?
くじに書かれた数字の合計を明らかにする問題でした。
対応関係の問題だと気づいたら、最初にすべきことは表のフォーマット作成です。
必要な情報をピックアップして、それらを一覧化しましょう。
必要な情報を見分ける方法の一つは、選択肢を見ることです。
本問であれば、選択肢のうち半分以上は最終結果(=数字の合計)に関する文言なので、各参加者の数字の合計を明らかにすることが一つのゴールになります。
そのために必要な情報は、ア〜クの数字がいくつで、それぞれ誰が引いたのか、ということなので、これらを含むようなフォーマットを用意すればOKです。
対応関係の出題パターンは多岐にわたるので、表の作り方も含め、慣れが必要な部分もあります。
今回紹介した「解法のポイント」も参考にしつつ、個々の問題からお決まりのパターンを抽出し、学んでいってください。
対応関係は、特に国家総合職では本当の本当に頻出なので、ここを攻略できれば高得点が期待できますよ。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
条件「ア、イ、ウを引いた者の人数は、それぞれ2人ずつであった。」および「aについて、AとFはイを引き、CとEはウを引いた。」より、BとDはアを引いたことになる。
条件「エ、オ、カを引いた者の人数は、それぞれ2人ずつであった。」および「bについて、AとDはオを引き、BとCはエを引いた。」より、EとFはカを引いたことになる。
ここまでを表にすると次のようになる。

aとbについて分かることを記入
条件「cから引いたくじが一致した3人は、aとbからは異なるくじを引いた。」に基づき、aでもbでも引いたくじが被らないような3人を選び出すと、AとBとEが該当する。
これより、AとBとEはキとクの一方を引いて、CとDとFはもう一方を引いたことが分かる。
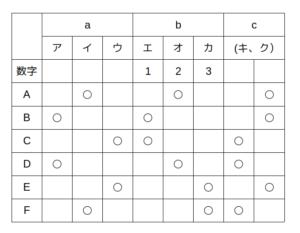
cについて分かることを記入
条件「各自がaとbから引いたくじの数字の和は、Cが5、Eが7、Fが6であった。」と表より、Eはbで3を引いているので、aでは4を引いたことになる。
Eがaで引いたのはウなので、ウは4と決まる。
このことと、条件「アとウの数字の差は2であった。」より、アは2と決まる。
これとFのa+bが6であること、Fがbで3を引いていることより、Fはaでは3(=イ)を引いたことになる。
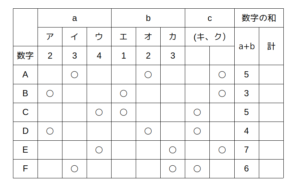
a+bまでの結果を記入
この表と、条件「BとCの順位は同じであった。」より、キが1、クが3となる。
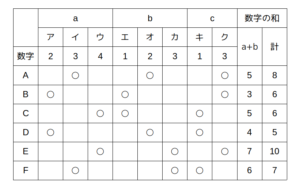
表が完成
この結果をもとに選択肢を検討すると、確実に正しいといえるのは5しかない。
したがって、5が正解である。

コメント