【国家一般職】数的処理の場合の数（＆確率）の攻略法を５つ紹介【保護者を含むグループに分ける場合の数】

こんにちは！
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。

公務員試験を受ける方は必見！
ぜひ最後まで読んでいってください。

今回のテーマは……「確率・場合の数」
まずは本サイトの肝である「解法のポイント」を紹介。
絶対に、これだけは覚えていってください。

この「解法のポイント」について、詳しく知りたい方は以下の記事をチェック。

ぶっちゃけて言うと、これだけでこの記事の半分はおしまい。
ほら、時間的な感覚だと人生の折り返しは２０歳っていうし。

ここからは、過去問をもとに作ったオリジナルの演習問題を解きながら、「解法のポイント」の使い方を学んでいきます。

演習問題：保護者を含むグループに分ける場合の数

特定の人を含むグループ分けの問題。
グループ分けの条件をうまく読みかえるのがカギ。

以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。

おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

それでは、解説スタート！

問題文を見る

解説：余事象の場合の数を引く

問題文をよく読むと、「グループには必ず１人以上の保護者を含める〜」という記述があります。
これは、「『少なくとも』１人以上の保護者を〜」と言い換えてもいいでしょう。

イメージしやすいように図を描いてみます。

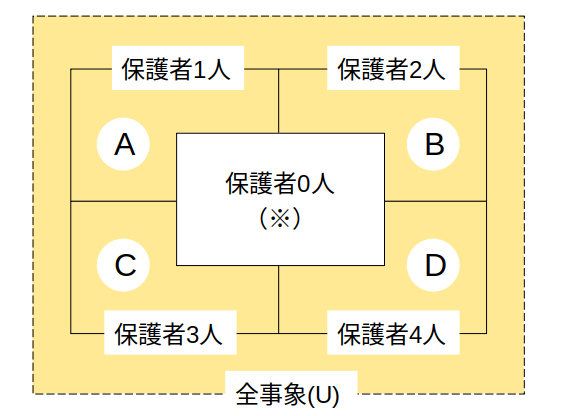
全事象Uは、保護者がグループに０〜４人いる場合の数を合計したものです。

図のように、「１人以上の保護者」を含む場合の数（オレンジ）は、全体から（※）を引くことで求められます。
つまり、「Uー（※）」です。

というわけで、全体から余事象を引く解き方でいきます。

組み合わせで余事象をカウント

まず全事象をカウントします。

保護者と児童の計１２人から４人を選ぶ選び方は、
\({}_{12} \mathrm{C}_4=495\)通り

本問でいう余事象は、「保護者が１人もいないグループ」のこと。
つまり、４人とも児童からなるグループです。

児童８人から４人選ぶ選び方は、
\({}_8 \mathrm{C}_4=70\)通り

これを全事象から引き算すればOK。

１人以上の保護者を含むグループの選び方は、
\(495-70=425\)通り

よって、２が正解です。

別解：場合分けによる正面突破も可能

ちなみに、余事象を使わないで解くこともできます。
その場合は、グループにいる保護者の人数（１人 or ２人 or ３人 or ４人）で場合分けして足し合わせればOKです。
解説は読者に委ねます。

この先はきみ自身の目で確かめてくれ！

おわりに：場合の数の「少なくとも」は余事象で

お疲れ様でした！

保護者を含むグループを作る問題でした。
確率や場合の数で「少なくとも」という表現があったら、余事象が近道です。
易しめの問題なので、確実に正解したいところ。

オマケのもう一問↓

最後までお読みいただきありがとうございました。

本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！

この記事が参考になったら、ぜひシェアしてください！

Tweet

次回もお楽しみに！

略解