こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
失敗しても、めげずに挑戦し続けられる自分でありたい。
前回は、市庁舎の建設にかかる費用の負担額を求める問題をやりましたね。
数的処理の問題全てに通用する、問題を解くための基本姿勢を再確認できる内容になってますので、解いてない方はぜひ挑戦してみてください。
もう解いた方も、時間をおいて再度チャレンジしてください。
そこできちんと解答までたどり着ければ文句なしですが、多くの場合、思わぬ壁にぶつかって最後まで解ききれないと思います。
手が止まったら、分からなかったところを中心にもう一度解説を読み込んでみてください。
きっと、1回目とは異なる視点から検証できている自分に気づくと思います。
これを繰り返すことで、解法への理解が深まり、初見の問題にも応用できるようになります。
1度だけ解いて満足してしまうのはもったいないことです。
せっかく苦労して学んだ解法を道具として使いこなすためにも、解き直し(復習)を忘れずに。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
1から100までの異なる整数が1つずつ書かれた計100個の箱がある。いま、それぞれの箱に書かれた整数の数だけ球が入った状態から始めて、以下の操作を、整数\(n\)を1, 2, 3, ……, 99, 100と変化させて順次行う。
操作:\(n\)で割り切れる整数が書かれた箱全てに球を1個ずつ加える。
全ての操作を終えた後に、箱の中の球の個数が偶数である箱は全部でいくつか。
- 34個
- 38個
- 42個
- 46個
- 50個
5
1から100までの整数を順次割り算していき、割り切れる箱にだけ球を追加する問題です。
球を加える操作がもつ意味を考えてみるとよいでしょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
さすがに、100個もある箱の中身を具体的に把握するわけにもいかないですよね。
ので、ここでいう「操作」がどんな意味を持っているのか(何か規則性はないか、など)を考えてみることにしましょう。
例えば「12」と書かれた箱なら、中身が増えるのは\(n=1, 2, 3, 4, 6, 12\)のときです。
これはつまり、「\(n\)が箱に書かれた整数の約数であるときだけ球を追加せよ」という操作であることを示します。
個数ベースで考えると、全ての操作が終わったとき、\(N\)番の箱には\(N\)の約数の個数だけ球が追加されていることになります。
注意すべきは、初期の状態ですでに\(N\)個の球が入っていることです。
すなわち、操作終了後の球の個数は「\(N\)+(\(N\)の約数の個数)」……(☆)で与えられるので、「1から100までの整数\(N\)のうちで、☆が偶数となる\(N\)はいくつあるか」というのが本問の主旨です。
☆の奇偶を判断するには、「\(N\)の約数の個数」の奇偶を知る必要があるので、これを調べましょう。
さて、整数の約数の個数は原則として偶数個となります。
これは、例えば「12」であれば、次図のようにして乗算の相方が決まることを考えれば容易に納得できるでしょう。
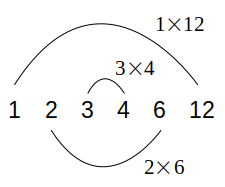
ただし、これはあくまで「原則として」の話でして、当然例外(=奇数個の約数を持つパターン)はあります。
それがどんな場合か、思いつきますか?
ここをクリアできれば、解答に至るのもそう難しい話ではなくなります。
答えを言いますと、平方数だけは例外となります。
次図は「16」を例に表したものですが、平方数の場合、真ん中にくる約数の相方が自分自身になるからですね。
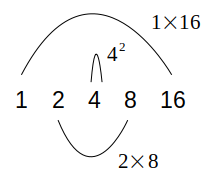
1〜100までの整数に含まれる平方数の約数の個数を調べると、次の通りになります。
\(1^2=1\) → 1個
\(2^2=4\) → 3個
\(3^2=9\) → 3個
\(4^2=16\) → 5個
\(5^2=25\) → 3個
\(6^2=36\) → 9個
\(7^2=49\) → 3個
\(8^2=64\) → 7個
\(9^2=81\) → 5個
\({10}^2=100\) → 9個
箱の中身は、「\(N\)+(\(N\)の約数の個数)」……(☆)で決まるんでしたね。
すると、上に列挙した平方数のうち、☆が偶数となるのは\(N\)が奇数のときなので、\(1^2, 3^2, 5^2, 7^2, 9^2\)の5つが該当します。
残り90個の箱についても同じように考えることができます。
今度は\(N\)が偶数の場合を数えます。(約数の個数が偶数なので)
残り90個の整数の中に、偶数は45個存在するので、これが該当する箱の数になります。
以上より、操作終了後の箱の中身が偶数である箱の数は、5+45=50個です。
よって、5が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
約数の個数を数える問題でした。
解説では「12」を例に、球が加えられるときの\(n\)の値を列挙し、操作の背景にある意味を汲み取ることから始めています。
12だけで分からなければ、他の整数も調べましょう。
いくつかの整数について、球が加えられるときの\(n\)を書き出せば、\(n\)が約数のときのみ操作が行われることが分かるかと思います。
あとは約数の個数の奇偶ですが、平方数だけは奇数個の約数を持つことに気づかなければなりません。
解説を読めばいたって単純な理屈ですが、似たような問題を解いた経験がないと、初見で気づくのはちょっと難しいかもしれませんね。
「約数の個数は原則として偶数」というのは、この機会に頭の片隅に入れてしまいましょう。
ちなみに、(奇数)+(奇数)および(偶数)+(偶数)はともに偶数で、(奇数)+(偶数)は奇数となります。
解説では特に断りなく使ってますが、整数のもつ重要な性質の一つです。
(あえて説明するまでもないとは思ったのですが、私が持っている参考書には重要事項として載っていたので、念のため書きました)
国家総合職の数的処理では、整数の性質を扱った問題は高い頻度で出題されています。
整数問題で一番多く用いられる解法は、不等式で範囲を絞り込んでしらみ潰しする方法です。
本問のような整数の性質を全面に押し出した問題は、どちらかというとマイナーケースではありますが、現に出題された例がある以上、対策しておく方が望ましいでしょう。
参考書には必ず整数分野を専門に扱ったページがあるはずなので、それも活用して出題パターンを把握しておくようにしてください。
本サイトでも、過去にいくつか整数の問題を扱っているので、こちらからチェックしてみてください。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
球を追加する操作のもつ意味を解釈すると、「\(n\)が箱に書かれた整数の約数であるときだけ球を追加せよ」ということである。
つまり、全ての操作終了後の球の個数は「\(N\)+(\(N\)の約数の個数)」……(☆)で与えられる。
以下で、「\(N\)の約数の個数」の奇偶を調べる。
整数の約数の個数は原則として偶数であるが、平方数の場合は奇数となる。
よって、\(N\)が平方数の場合、☆が偶数となるのは\(N\)が奇数のときで、該当する箱は5個である。
それ以外(\(N\)が平方数でない場合)は\(N\)が偶数のときに☆が偶数となるので、該当する箱は45個である。
以上より、操作終了後の箱の中身が偶数である箱の数は、5+45=50個
よって、正解は5である。

コメント