こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「順序関係」
まずは本サイトの肝である「解法のポイント」を紹介。
自分なりの表現方法を用意しておく
- 順番だけ→○(マル)に書き込む
- 数的な差(高低が分かる)→数直線を書く
- 数的な差(高低が分からない)→Aを始点とした樹形図
この「解法のポイント」について、詳しく知りたい方は以下の記事をチェック。
ぶっちゃけて言うと、これだけでこの記事の半分はおしまい。
ほら、時間的な感覚だと人生の折り返しは20歳っていうし。

終了、解散!
ここからは、過去問をもとに作ったオリジナルの演習問題を解きながら、「解法のポイント」の使い方を学んでいきます。
演習問題:列車が駅にたどり着く順位
2つの駅PーQ間を走行する5つの列車A〜Eがある。いま、同時刻にP駅を発車したA〜Eが、いずれも通過駅であるR駅を通ってQ駅へ向かったとする。このときのA〜Eの乗客がそれぞれ次のように発言しているとき、CがR駅を通過した順位とBがQ駅に着いた順位の和はいくらか。
ただし、発言をした乗客の中にPーQ駅の間で途中下車した者はいなかったものとする。
また、列車の大きさは考慮せず、追い越す/抜かれるは瞬間的に起こるものとする。
A:RQ間で、Bに1回抜かれたあとBを1回追い越した。
B:RQ間で、列車を3台追い越したが2台に抜かれた。
C:RQ間で、1回だけ順位が変わった。先にQ駅に着いている列車があった。
D:先頭でR駅を通過したが、RQ間で車両点検のため一時停車した結果、最後にQ駅に着いた。
E:RQ間では常にAより前を走行していた。
- 4
- 5
- 6
- 7
- 8
5
列車が駅に着く順位の問題。
Q駅時点の順位から考えるのが良さそう?
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:図示しながら順序関係を整理
順序関係の「解法のポイント」を使います。
自分なりの表現方法を用意しておく
- 順番だけ→○(マル)に書き込む
- 数的な差(高低が分かる)→数直線を書く
- 数的な差(高低が分からない)→Aを始点とした樹形図
本問に数的な大小に関する情報はなく、単に順番だけが問題なので、【1】で考えます。
R駅時点の順位と、Q駅に着いたときの順位を別々に検討します。
発言から分かることを図示

まず、
Eの発言RQ間では常にAより前を走行していた
について。
これはQ駅に着くときにEの順位がAよりも上だったことを表します。
よって、Q駅時点の順位はE>A
もう一つ、この発言から、R駅の時点でEはすでにAより前を走っていたことも分かります。
つまり、R駅時点でもやはり順位はE>A
また、 Aの発言RQ間で、Bに1回抜かれたあとBを1回追い越した より、Q駅時点のAの順位はBよりも高く、A>B
これはR駅時点でも同様で、やはり順位はA>B

つまりR駅でもQ駅でもE>A>B
Dの発言先頭でR駅を通過したが、RQ間で車両点検のため一時停車した結果、最後にQ駅に着いた
は、読んで字のごとく。
つまり、R駅時点およびQ駅時点のDの順位はそれぞれ1位、5位です。
さらに、 Cの発言の後半〜。先にQ駅に着いている列車があった は、「CはQ駅時点で1位ではなかった」という意味。
ここまでを図示します。

Q駅に着いた順番

情報量の多いQ駅時点の順位から考えます。
まず、1位はC以外です。
また、E>A>Bの制約から、AとBが1位となることもありません。
すると、消去法でQ駅時点の1位はEに決まります。

Dは5位で確定してるからね
次に、
Bの発言RQ間で、列車を3台追い越したが2台に抜かれた
について考えてみます。
これより、Q駅時点で前に列車が2台以上あったことになります。
よってQ駅時点のBの順位は3位以下、つまり3位か4位です。

これは、3歩進んで2歩下がる的なヤツだ(違う)
仮にQ駅時点で4位だったとしてみます。
このとき、AとCが2位と3位のいずれかです。
この段階で、Bが追い越した3台はAとCとD、抜かれた2台はAとCに決まります。
しかし、これは
Cの発言の前半RQ間で、1回だけ順位が変わった。〜
に矛盾します。
CはBに抜かれたあとBを追い越して、順位が2回変わったことになるからです。

Dも抜いてるから正確には計3回
これにより、Q駅時点のBの順位は3位となります。(R駅時点では1つ下の4位)
すると、E>A>BよりAが2位、残ったCが4位と決まります。
ここまでを図にします。

Q駅時点の順位が確定しました。
あとはR駅時点の順位です。
R駅に着いた順序
E>A>Bの関係より、Eが2位でAが3位。
残ったCが5位となります。
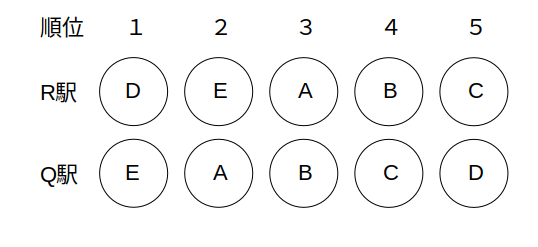
表が完成しました。
これより、5+3=8
よって、5が正解です。
おわりに:順序関係には「図示」が有効
お疲れ様でした!
列車が駅に着いた順番を検討する、順序関係の問題でした。
本問のように、数的な情報を伴わない場合は○(マル)に書き込むやり方がオススメ。
条件から分かったことがあれば、都度可視化しましょう。
解説では「E>A>B」などと表しましたが、決まりはないので自分が分かれば何でもOK。
「こだま」よりも「ひかり」よりも速いのが「のぞみ」ってアツい

突き進めば希望(のぞみ)はかなう
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
Eの発言「RQ間では常にAより前を走行していた」より、Q駅時点の順位はE>A
これはR駅の時点でも同じなので、R駅時点でも順位はE>A
Aの発言「RQ間で、Bに1回抜かれたあとBを1回追い越した」より、Q駅時点の順位はA>B
これはR駅時点でも同じで、順位はA>B
Dの発言「先頭でR駅を通過したが、RQ間で車両点検のため一時停車した結果、最後にQ駅に着いた」より、
R駅時点およびQ駅時点のDの順位はそれぞれ1位、5位。
Cの発言の後半「〜。先にQ駅に着いている列車があった」より、Q駅時点でCは1位ではない。

列車の順位を○の並びで表現
Q駅時点の順位について、Cは1位ではない。
また、E>A>Bの制約から、AとBが1位となることもない。
よって、Q駅時点の1位はEに決まる。
Bの発言「RQ間で、列車を3台追い越したが2台に抜かれた」について、Q駅時点のBの順位は3位以下、つまり3位か4位となる。
仮にQ駅時点でBが4位だったとすると、Bが追い越した3台はAとCとD、抜かれた2台はAとCに決まる。
しかし、これはCの発言の前半「RQ間で、1回だけ順位が変わった。〜」に矛盾する。
(CはBに抜かれたあとBを追い越して、順位が2回変わったことになるため)
よって、Q駅時点のBの順位は3位となる。(R駅時点では1つ下の4位)
すると、E>A>Bより、Q駅時点ではAが2位、残ったCが4位と決まる。

Q駅時点の順位が確定
R駅時点の順位について、E>A>Bの関係より、Eが2位でAが3位である。
残ったCは5位となる。

R駅時点の順位が確定
これより、5+3=8
よって、5が正解である。




コメント