- 数的処理で頻出の順序関係を解くためのコツが分かる
- 過去問の類題を例に、本番で役立つ「解法のポイント」の使い方を学べる
- どこよりも詳しい解説で、本試験レベルの問題を完全理解
→数的処理の「あと一点」が実現!
こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
今回のテーマは「順序関係」です。
順序関係は、対応関係や位置関係と並ぶ判断推理の超頻出分野です。
頻出なだけに問題のバリエーションも多岐にわたり、なかなか捉え所のない分野だったりもします。
「問題演習の量が大切だから」と多くの問題にあたるも、結局は解法の丸暗記に終始してしまいがちです。
これでは場当たり的な解き方の知識が増えるばかりで、初見の問題に対応できず、挫折してしまうこともあるでしょう。
しかし、これを読んでいる方は大丈夫。
順序関係にも典型的な解き方は存在します。
この記事で取り上げる、多くの問題に共通する解法のパターンを学べば、正解にグッと近づけます。
この記事では、数的処理の「速さ」に関する問題を解くためのコツである「解法のポイント」を紹介します。
それから過去問の類題を一緒に解いて理解してもらうことで、本番で使える解法を身につけていってもらいます!
講義:順序関係の解き方のコツ
順序関係のコツは「図示して考えること」です。
自分なりの表現方法を用意しておく
- 順番だけ→○(マル)に書き込む
- 数的な差(高低が分かる)→数直線を書く
- 数的な差(高低が分からない)→Aを始点とした樹形図
対応関係が「表」なら、順序関係は「図」が肝心です。
可視化することで、条件同士の関係に気づけたり、場合分けの見通しを立てやすくなります。
順序関係を解くときは、図示して考える習慣をつけてください。

対応関係の攻略法は以下の記事をみてね
図示して考えるときは、自分なりの表現方法を持っておくといいです。
答えが分かればいいので、自分がしっくりくる書き方でOK。
「図をどう描いていいか分からない」という方も、参考書や問題集の書き方をマネていきましょう。
以下、図の描き方を3パターン紹介します。
【1】順番だけ→○(マル)に書き込む
最もオーソドックスなのは、○(マル)に書き込みながら考えるやり方です。
登場人物の数だけ○(マル)を用意して、確定したものから文字を書き込んでいきます。
例:「A〜Fの6人で、Bは3番目」なら…
○○○○○○
↑ここにBと記入
ほかの条件は、○に記入するための「パーツ」として表現します。
ありがちなのは次のようなものです。
A>B:AはBより上位
A○○B:AはBより3つ順位が高い(=AとBの間に2人いる)
パーツ化しておくと、条件同士の関係や場合分けの基準が見えやすくなります。
考える過程で決まることがあれば、その都度○に書き込んだりパーツ化していきます。

単に順番だけが問題ならこのやり方でOK
(問)
A、B、C、Dの4人が待ち合わせ場所に、4人とも異なった移動手段で到着した。
以下のことがわかっているとき、確実に正しいといえるものはどれか。
・移動手段はバス、タクシー、自転車、徒歩であった。
・Cの次の次の人はバスで来た。
・Bは徒歩で来た。
・タクシーで来た人の次にBが来た。
・Aが到着したのは最後ではない。
1 Aはバスで来た
2 Bは3番目に到着した
3 Aの次にCが到着した
4 Cが1番最初に到着した
5 Cはタクシーで来た(答)
今回は到着順と移動手段の2つがあるので、
1 2 3 4 のような表で考える。
Cの次の次の人はバスで来た →
C バス Bは徒歩できた →
B 徒歩 タクシーで来た人の次にBが来た →
B タクシー 徒歩 あとは、これらを組合せていけばよい。今回は、Aが最初か3番目かの2パターンできる。
1 2 3 4 A C B D 自転車 タクシー 徒歩 バス
1 2 3 4 C B A D タクシー 徒歩 バス 自転車 以上より、確実にいえるのは「Cはタクシーで来た」である。
公務員試験過去問 判断推理 順序関係|問題野郎
上の例題は、○の並びに記入するパターンの発展形です。
考え方は同じ。
始めに空白の表を用意し、「人」と「移動手段」の対応に関する条件をパーツ化しています。
Cの条件をパーツ化すると、Cの順位が1番が2番のいずれかしかないことが視覚的に分かります。

ジグソーパズルでピース(条件のパーツ)を当てはめるイメージ
【2】数的な差(高低が分かる)→数直線を書く
「身長が〜cm高い(低い)」とか「点数が〜点高い(低い)」といったように、数的な差が与えられて、かつ高いか低いかが分かっているような問題は、数直線で考えることができます。
例を見てみましょう。
(問)
5人にテストを行ったところ、次のような結果が出た。
・Aは、平均点より12点高かった。
・Bは、Eより4点高かった。
・Cは、Bより6点高かった。
・Dは、Cより14点低かった。
・Eは、Aより18点低かった。
このとき、正しいものはどれか。1.CはAより高い点数。
2.平均点より高いのは、A、B、Cである。
3.Dは平均点より10点低い。
4.Bはちょうど平均点である。
5.点数が最も高いのはAで、最も低いのはE。(答)
数直線を書き、平均点を中心に他の点数を調べる。以上より、正解は3である。
順位・順序(判断推理) – 公務員試験対策ノート –
上の例題では、A〜E同士の点差と高いか、低いかが与えられています。
平均点を基準に定め、1点刻みの数直線を書きます。
すると、平均点からAの位置(=点数)が決まります。
あとはE、B、……と芋づる式に数直線上の位置が決まり、5人の順序関係が明らかになります。

具体的な点数は分からなくてOK
【3】数的な差(高低が分からない)→Aを始点とした樹形図
【2】に対して、高い/低いの関係が不明なケースには樹形図です。
A(誰でもOK)を基準に置いて、
Bの高い/低いを場合分けして、Cの高い/低いを場合分けして、Dの……
というように枝分かれを書き出して検討します。
(問)
あるテストをA〜Eの5人が受けた。彼らのテストの点数について、次のア〜オのことがわかった。
ア AとBの点数の差は1点である。
イ BとCの点数の差は4点である。
ウ CとDの点数の差は3点である。
エ DとEの点数の差は4点である。
オ EとAの点数の差は2点である。
このとき、確実にいえることはどれか。
1.Aは3番目に点数が高い。
2.Bが3番目に点数が高いならば、最高点はEである。
3.Cは最高点ではない。
4.Dが2番目に点数が高いならば、最高点はBである。
5.Eは4番目ではない。(答)
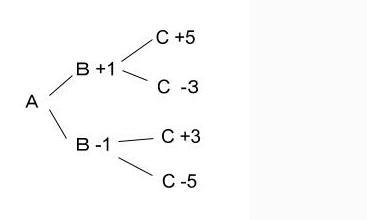
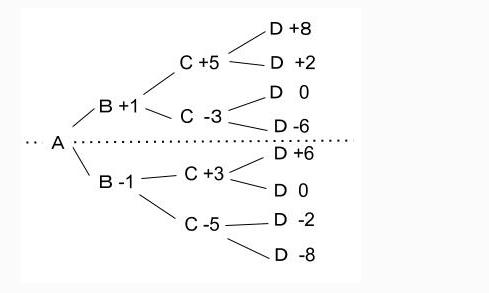
以下のようにかいていきます。下図はCまで書いたところです。さらにDまで書くと以下のようになります。
点線を対称軸として、上下でプラスマイナスを入れ替えれば対称になっていますね。
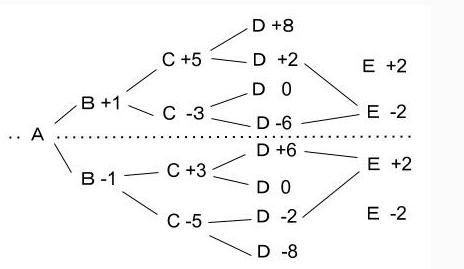
※これを利用すれば、上の分だけ書いて解答可能です。ゴールのEは、Aとの点差が2点なので、下図のようにしましょう。
DからEへの枝分かれをすべて書くのではなくて、うまくいくものだけを書くのです。以上、樹形図より、4通りの可能性があることがわかりました。
順に書きだします。前述の通りですが、①と④は符号の入れ替えをしただけのものです。
②と③も同様です。
樹形図は上半分だけ書いて、うまくいったものの符号替えも書けばOKです。この表を見ても、選択肢の検討はやりづらいですね。
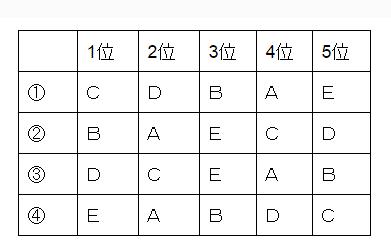
以下のように順位がわかるような表に書き換えます。①と④、②と③は互いに順位が真逆になっています。
これを見ながら選択肢を検討すれば、選択肢5 Eは4番目ではない。
【順序】問題2 | 公務員試験数的処理解法テクニック KOMARO
が正解とわかります。
上の例題は、点差は与えられてますが両者の高い/低いは分かりません。
こういう場合は樹形図が有効です。
樹形図を使って全てのケースを書き出して検討します。
演習問題:円卓における水差しの受け渡し
図のようなA〜Iの9人が座る円卓において、①および②に示す手順で水差しの受け渡しが行われた。
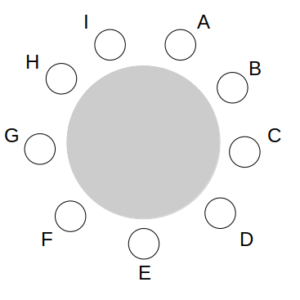
①:B、E、Hの3人の間で水差しの受け渡しがあった。始めに水差しを持っていたのはBで、E、Hがそれぞれ1回ずつ水差しを受け取ったあと、水差しはBのもとへ戻った。
②:B、E、Hを除いた6人の間で水差しの受け渡しがあった。始めに水差しを持っていたのはAで、A以外の5人がそれぞれ1回ずつ水差しを受け取ったあと、水差しはAのもとへ戻った。
次のことが分かっているとき、確実に正しいといえるのはどれか。
- ①においてBから水差しを受け取った者の右隣は、②においてAへ水差しを渡した者であった。
- ②において、水差しをAから受け取った者とAへ渡した者は隣り合っていた。
- ②において、水差しを渡した者と受け取った者の間には、左右どちらも2人分以上の間隔が空いていた。(例えば、AはB、C、I、Hのいずれにも水差しを渡したということはなかった。)
- CはGへ水差しを渡した。
- DはAへ水差しを渡した。
- EはHへ水差しを渡した。
- FはCへ水差しを渡した。
- GはDへ水差しを渡した。
4
円卓に座った者同士で水差しをパスし合う問題です。
「講義」で扱ったパターンのうち、どれが使えるでしょうか?
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説:円卓に数字を書き込んで検討する
やはり図を描いて考えます。
円卓の見取り図が与えられてますから、これを使います。
水差しを受け取った順番を、座席の○(マル)に書き込みます。
①については一〜三、②については1〜6と、それぞれ表記します。
「講義」の項で言うと、【1】のパターンに当たります。
自分なりの表現方法を用意しておく
- 順番だけ→○(マル)に書き込む
- 数的な差(高低が分かる)→数直線を書く
- 数的な差(高低が分からない)→Aを始点とした樹形図
①はB、E、Hの3人による受け渡しです。
Bから始まってBで終わり、その間にEとHが1回ずつ受け取るので、次の2通りの順序があります。
(i)BEHB
(ii)BHEB

「B→○→○→B」のマルにEとHを並べるから2!通り
以下、それぞれのケースを検討します。
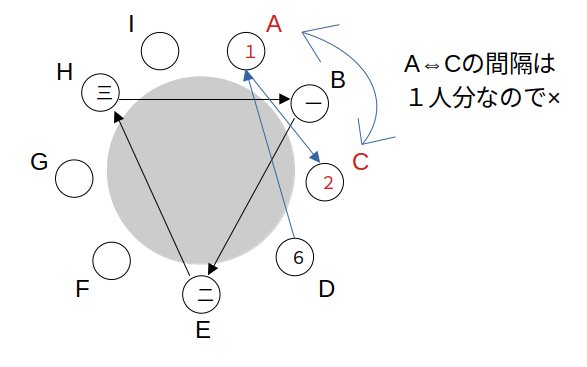
(i)BEHBという順序→×
1つ目の条件①においてBから水差しを受け取った者の右隣は、②においてAへ水差しを渡した者であった より、②で「Aへ水差しを渡した者」はDとなります。
すると、 2つ目の条件②において、水差しをAから受け取った者とAへ渡した者は隣り合っていた より、②で「Aから受け取った者」はCです。
ところがこの場合、AC間は1人分で 3つ目の条件②において、水差しを渡した者と受け取った者の間には、左右どちらも2人分以上の間隔が空いていた に反します。

「AはB、C、I、Hのいずれにも水差しを渡したということはなかった」ってちゃんと書いてある
よって、BEHBという順序は不適。
(ii)BHEBという順序:条件で絞り込んで総当たり 樹形図も有効
同様に考えると、②で「Aへ水差しを渡した者」はG、「Aから受け取った者」はFです。
つまり「A→F→○→○→○→G→A」です。
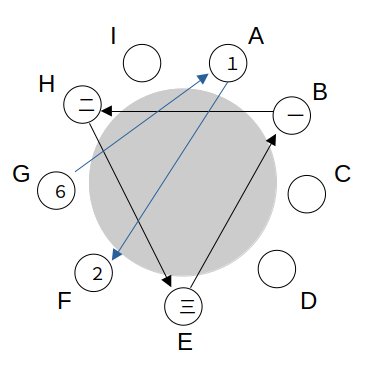
あとは条件に基づいてあり得るケースを調べるだけです。
Fの次に受け取る可能性があるのはCかIです。
Cの場合、やはり
3つ目の条件②において、水差しを渡した者と受け取った者の間には、左右どちらも2人分以上の間隔が空いていた
からI→Dとなり、G→Aとつながります。
Iの場合、次はCかDですが、いずれもその次がGしかなくG→Aへつながらないので不適。
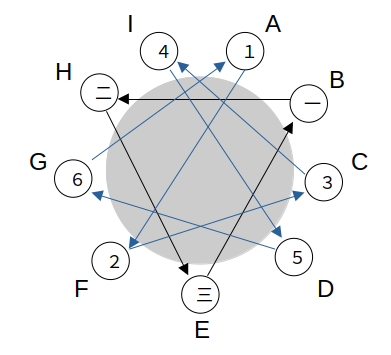

ここは樹形図を描くと分かりやすい
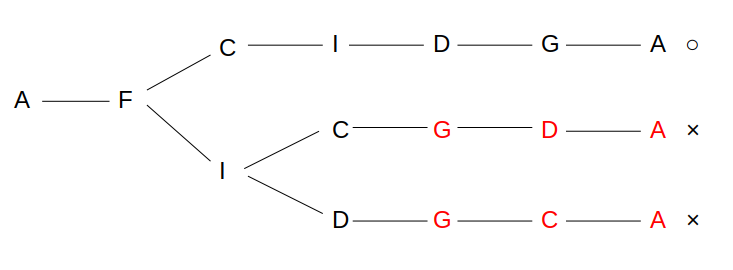
全部でもたかだか3!=6通りなので、しらみつぶししてもOKです。
その場合は、全て書き出して条件に合わないパターンを消し込む、というやり方になります。
樹形図で表すとミスなく書き出せます。
結局、条件を満たすのは①でBHEB、②でAFCIDGAとなるパターンだけです。
よって、4が正解です。
おわりに:順序関係は○(マル)に書き込んで考えるのがコツ
お疲れ様でした!
いかがだったでしょうか?
順序関係は図を描いて視覚的に捉えるのが有効です。
○(マル)に書き込んだり、数直線や樹形図で表す方法を問題によって使い分けしましょう。
今回は、水差しの受け渡しの順序を調べる問題でした。
「講義」の項で紹介した、○(マル)に書き込むパターンの一種です。
①の2通りに対し、条件を満たす②の受け渡しの順番を調べます。
後半は書き出してしらみつぶしするのも大いにアリです。

むしろ書き出した方がミスしにくいまである
冬物をいつしまえばいいか誰か教えて
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
①のB、E、Hの3人による受け渡しの順序は、(i)BEHBまたは(ii)BHEBのいずれかである。
(i)BEHBのとき→×
1つ目の条件「①においてBから水差しを受け取った者の右隣は、②においてAへ水差しを渡した者であった」より、②で「Aへ水差しを渡した者」はDである。
2つ目の条件「②において、水差しをAから受け取った者とAへ渡した者は隣り合っていた」より、②で「Aから受け取った者」はCである。
ところがこの場合、AC間は1人分なので3つ目の条件「②において、水差しを渡した者と受け取った者の間には、左右どちらも2人分以上の間隔が空いていた」に反する。
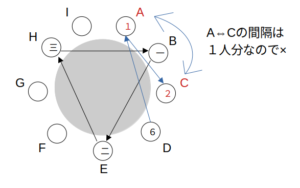
BEHB→条件を満たさない
(ii)BHEBのとき
②で「Aへ水差しを渡した者」はG、「Aから受け取った者」はFである。
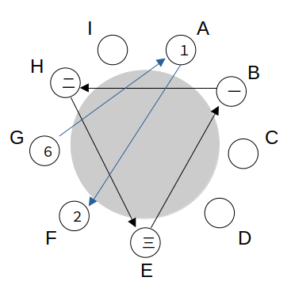
BHEBのとき2番目はF、6番目はG
このとき、全ての条件を満たすのはAFCIDGAの順番だけである。
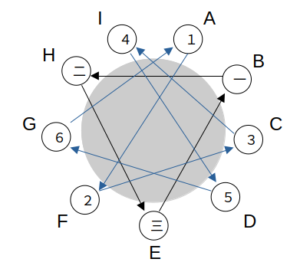
AFCIDGAであれば条件を満たす
したがって、4が正解である。



コメント