- 立方体の切り口の形が描けるようになる
- 過去問の類題を例に、本番で役立つ「解法のポイント」の使い方を学べる
- どこよりも詳しい解説で、本試験レベルの問題を完全理解
→数的処理の「あと一点」が実現!
こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
今回のテーマは「空間図形」です。
本サイトでは、過去に「切り口」と「展開図」の考え方を詳しく解説しました。
ともに空間図形では頻出のテーマなので、まだ読んでない方にはオススメです。
講義:空間図形の切り口の描き方
空間図形の切り口は、次の3ステップに従えば、誰でも、機械的に描くことができます。
- 同一平面上の点を結ぶ
- 平行な面上の辺を平行に引く
- 切り口の辺を延長しxyz軸との交点を考える
以下、立方体の切断を例に1ステップずつ説明します。
【1】同一平面上の点を結ぶ
切断面を通る3点が与えられたら、まずすることは「同一平面上の点同士を結ぶこと」です。
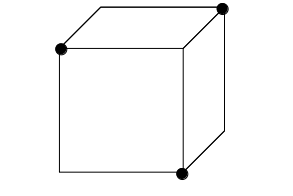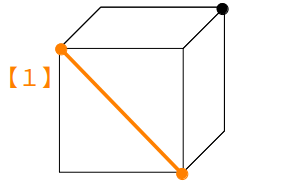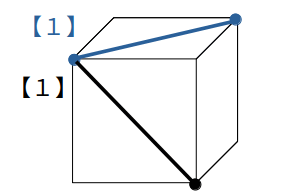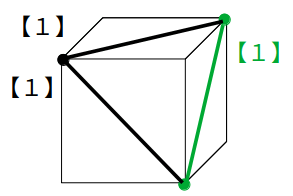
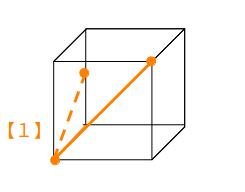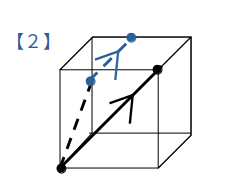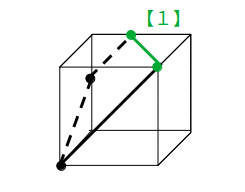
例えば、次図のように立方体の3頂点を含む平面で切断することを考えます。
この場合、【1】の「同一平面上の点を結ぶ」を使うだけで切り口が分かります。
【2】平行な面上の辺を平行に引く
【1】で結べない点があった場合は、【2】の方法を使います。
向かい合う面上の辺に対して平行に、立方体の一辺にぶつかるまで線を引きます。
ぶつかった点と、結べなかった点が同一平面上にあれば、再び【1】で切り口を描けます。
例えば、次図のように立方体の2頂点と辺上の1点を含む平面による切断を考えます。
この場合、まずは【1】を使って同一平面上の2点同士を結びます。
そこから【2】を使い、立方体の辺にぶつかるまで線を引くと、ぶつかった点は1頂点と同一平面上なので、【1】により切り口(台形)が完成します。
【2】を使って切り口を描く例をもう一つ。
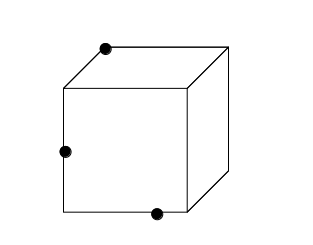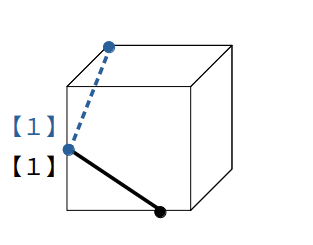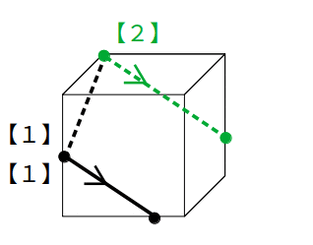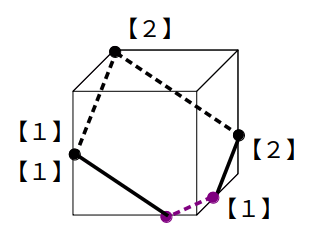
次図のように、立方体の辺上にある2点と1頂点を通る平面で切断することを考えます。
この場合、まずは【1】を使って点を結びます。
その後、向かい合う面上にある線分と平行に、立方体の一辺にぶつかるまで線を引きます。
これを2回行うと、同一平面上に2点が残るので、あとは再び【1】を使えば切り口(五角形)が描けます。
【3】切り口の辺を延長しxyz軸との交点を考える
【1】でも【2】でも解決できないときには、【3】の方法です。
この方法が有効なのは、立方体では次のような、3点が全て辺上にあるケースのみです。
この場合、切り口は六角形となります。
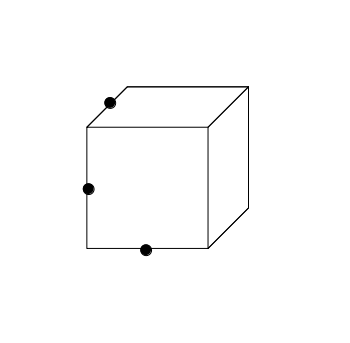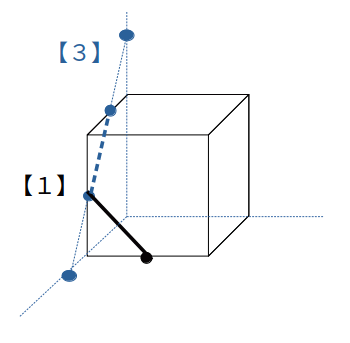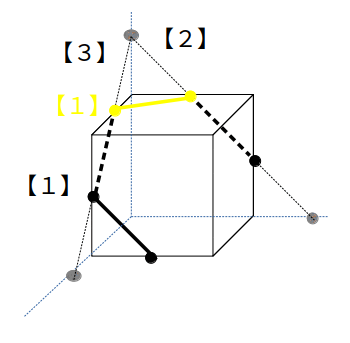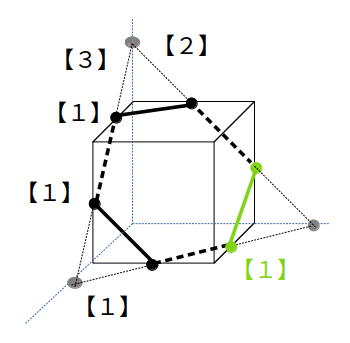

これ以外は【1】と【2】だけで解決できるよ
演習問題:立方体の切り口の形状
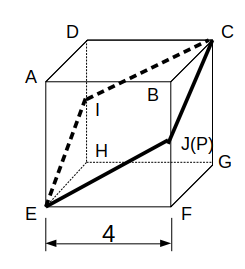
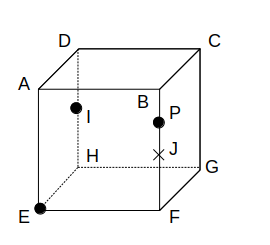
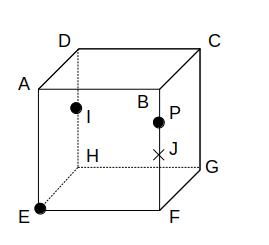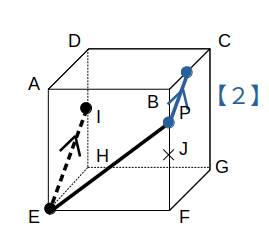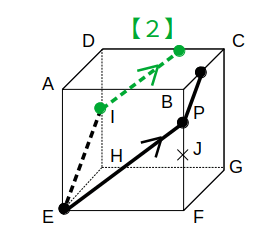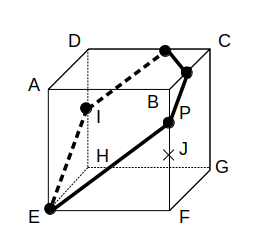
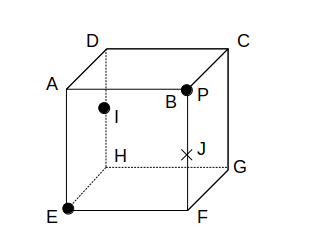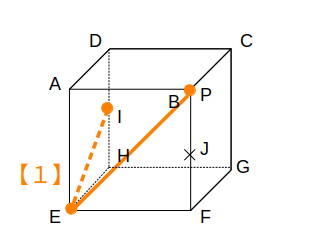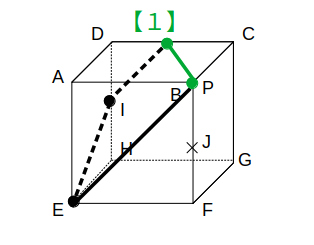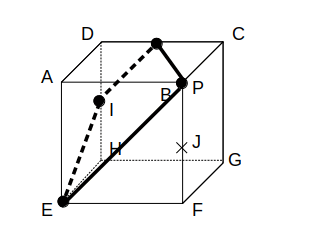
図のような1辺の長さが4の立方体ABCDーEFGHにおいて、辺DHおよびBFの中点をそれぞれI、Jとする。この立方体において、線分BJ上を自由に動く点をPとして、3点E、I、Pを通る平面で立方体を切断したときの断面を考える。このとき、切断面の形状としてあり得るものをア〜カより全て挙げたものとして正しいのは、次のうちどれか。
ただし、図の状態(点Pが点J上にある状態)は除くとする。
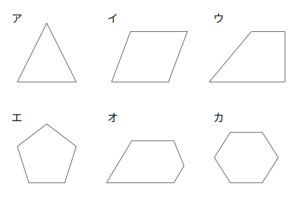
- アとウ
- アとエとカ
- イとエ
- イとオとカ
- ウとオ
5
立方体の切断面の形状を問う問題です。
「講義」で扱った切り口の描き方が威力を発揮します。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説:場合分けして切り口を描く
点Pが線分BJ上を動くとき、つねに「EP>EI」なので、ア(正三角形)、エ(正五角形)、カ(正六角形)は候補から外れます。
点Pが、中点Jを出発して頂点Bまで動くとき、「点Pが頂点にあるか否か」で状況が変わります。
つまり、次の2つのケースに分けて考えればOKです。
(i)J<P<Bのとき
(ii)P=Bのとき
各パターンにおける切り口の形は、講義の項で紹介した「解法のポイント」を使って描くことができます。
- 同一平面上の点を結ぶ
- 平行な面上の辺を平行に引く
- 切り口の辺を延長しxyz軸との交点を考える
(i)J<P<Bのとき:2組の平行な辺をもつ五角形
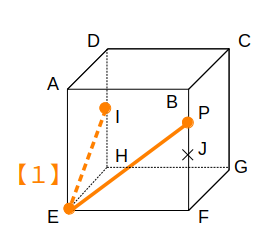
次図の状態からスタートします。
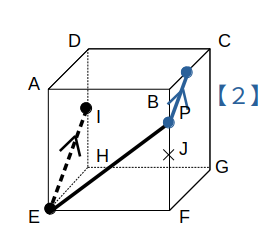
まず、【1】を使って同一平面上の点を結びます。
ここからは【2】です。
点Pから、EIに平行に線を描きます。
さらに、点Iから、EPに平行な線を描きます。
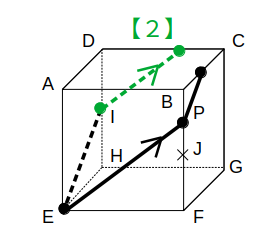
残った点は同一平面上なので、【1】を使えば切り口が完成します。
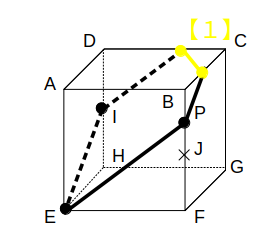
これは選択肢のオ(2組の平行な辺をもつ五角形)に他なりません。
(ii)P=Bのとき:台形
同じように、「解法のポイント」を使って切り口を描きます。
次図の状態からスタートします。
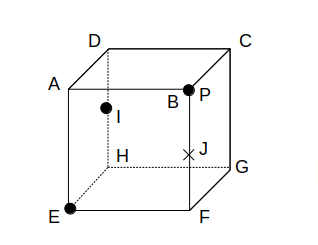
まず、【1】を使って同一平面上の点を結びます。
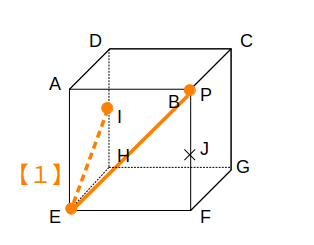
【2】を使って、点IからEPに平行な線を描きます。
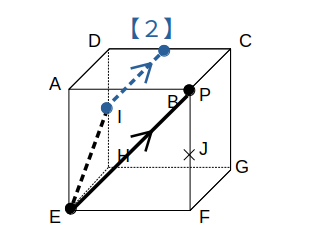
残った点は同一平面上なので、【1】を使うと切り口が完成します。
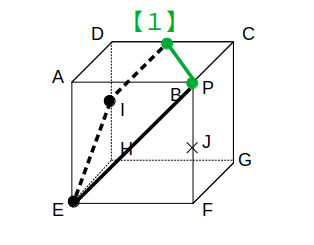
切り口は台形で、選択肢ではウに他なりません。
以上、切り口の形であり得るのはウとオです。
よって、5が正解です。
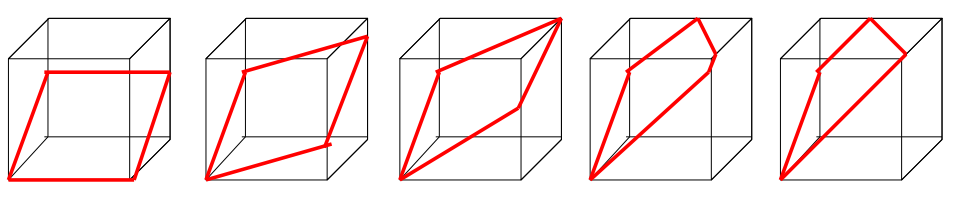
ちなみに、点Pが辺BF上を動くと、切り口は次のように変化します。

イ(平行四辺形)はF≦P≦Jのときなので本問では候補外
おわりに:切り口は同一平面上を結び平行線を描く
お疲れ様でした!
立方体の切り口は、機械的に描くことができます。
同一平面上を結んで平行線を描く、それでもダメなら軸との交点を考える、です。
立方体以外の立体でも、このやり方は通用します。

本問の元ネタは直方体だったけど、その場合でも解き方は同じ
今回は、固定した2点と動く1点からなる平面による立方体の切り口を考える問題でした。
点Pが線分BJの端点にあるときとその中間にあるときで状況が変わることに気づけたでしょうか?
場合分けしたら、あとは「解法のポイント」を使って切り口を描けばOKです。
「解法のポイント」はよく知られた方法なので、知識として身につけておいてください。

切り口はイメージと違ったりするから、ちゃんとやり方を覚えるのが大切
gif作るの思ったより時間かかった
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
点Pが線分BJ上を動くとき、つねに「EP>EI」であるから、アとエとカは不適。
あとは「点Pが頂点にあるか否か」で場合分けする。
(i)J<P<Bのとき
次図のように、切り口は2組の平行な辺をもつ五角形となる。

切り口は2組の平行な辺をもつ五角形
(ii)P=Bのとき
次図のように、切り口は台形となる。
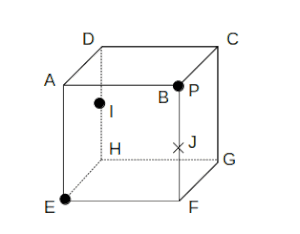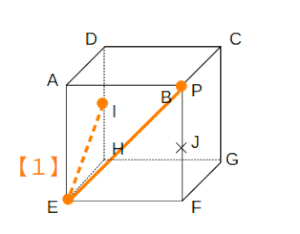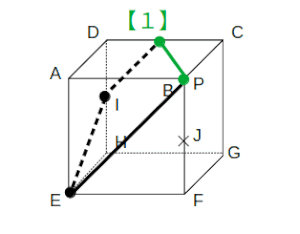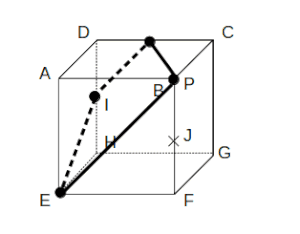
切り口は台形
以上より、切り口の形としてあり得るのはウとオ。
したがって、5が正解である。

コメント