こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
暖かくなる前に冷蔵庫を買いたい。
- 空間図形の攻略に役立つ考え方が身につく
- 過去問の類題を例に、本番で役立つ「解法のポイント」の使い方を学べる
- どこよりも詳しい解説で、本試験レベルの問題を完全理解
→数的処理の「あと一点」が実現!
数的処理の対策なら、空間図形を勉強しましょう。
理由は2つ。
- 例年1〜2問、1問はほぼ固定で出題がある
- 捨て問にする人が多いため、差が付きやすい
「空間図形はセンスが必要だから」と、捨ててしまう方は多くいます。
たしかに、空間図形は平面に比べて考えないといけない要素が多く、苦手な方には難しい部分もあります。

表から見えない裏側を想像しなくちゃいけなかったりするよね
しかし、基礎となる考え方さえ知っていれば対処できる空間図形の問題もあります。
それに、多くの人が諦めてしまう分野を盤石にできれば大きなアドバンテージになりますよね。
この記事では、公務員試験の数的処理で出題される空間図形の問題に広く応用可能な「解法のポイント」を紹介します。
それから過去問の類題を一緒に解いて理解していただくことで、本番で使える解法を身につけていってもらいます!
講義:空間図形のコツは「平面で捉えること」
空間図形の問題を解くコツはこれ。
適切な切り口を設定しよう
平面図形でいう補助線のように、適切な面で切ってあげましょう。
平面ならば、使える道具(=定理や法則)が多いので見通しが良くなることがあります。
ただし、「どんな平面で切るか?」という点は重要です。
ここを一般化するのはなかなか難しいんですが、迷ったらまずは軸に関して特徴的な平面で切ってみるのがオススメです。
特徴的な平面、というのは、(i)軸に垂直か、あるいは(ii)軸に平行な平面、のことです。

(ii)は軸を含む平面のことね
例題として、立体の切断が有効なケースを紹介します。
(問)
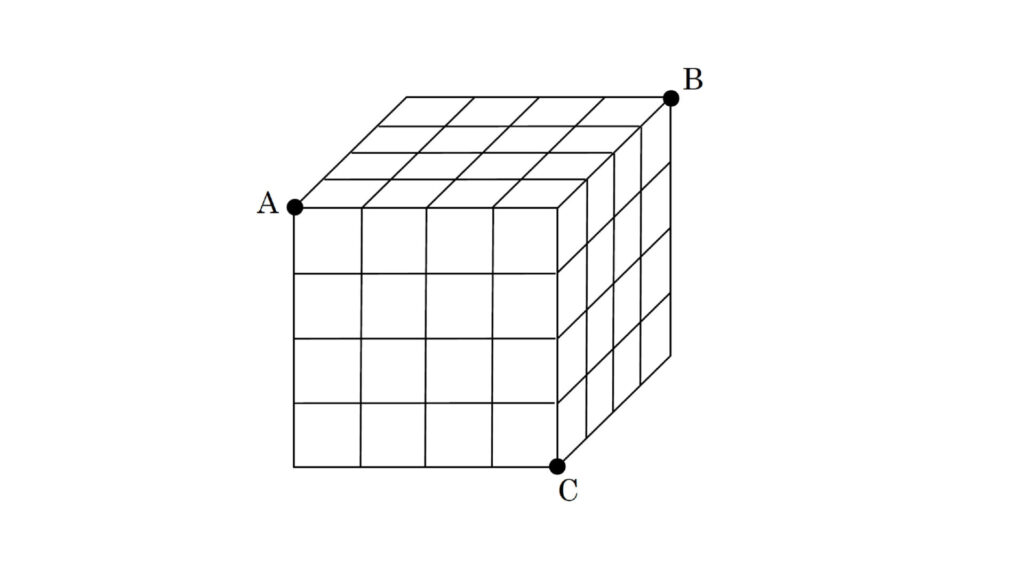
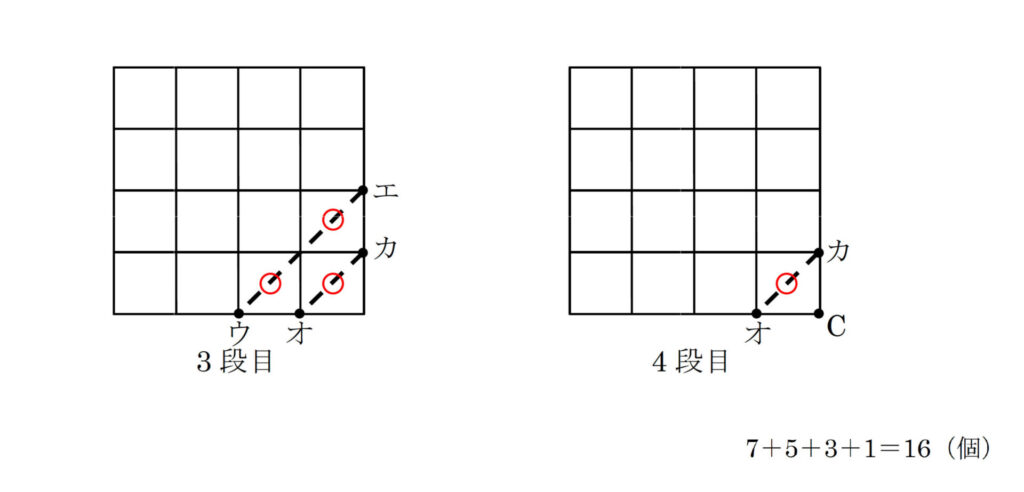
下の図のように同じ小さい立方体を64個積み重ねて大きい立方体を作ります。3つの頂点A, B, Cを通る平面でこの大きい立方体を切ったとき、切られた小さい立方体は何個ありますか。
(答)
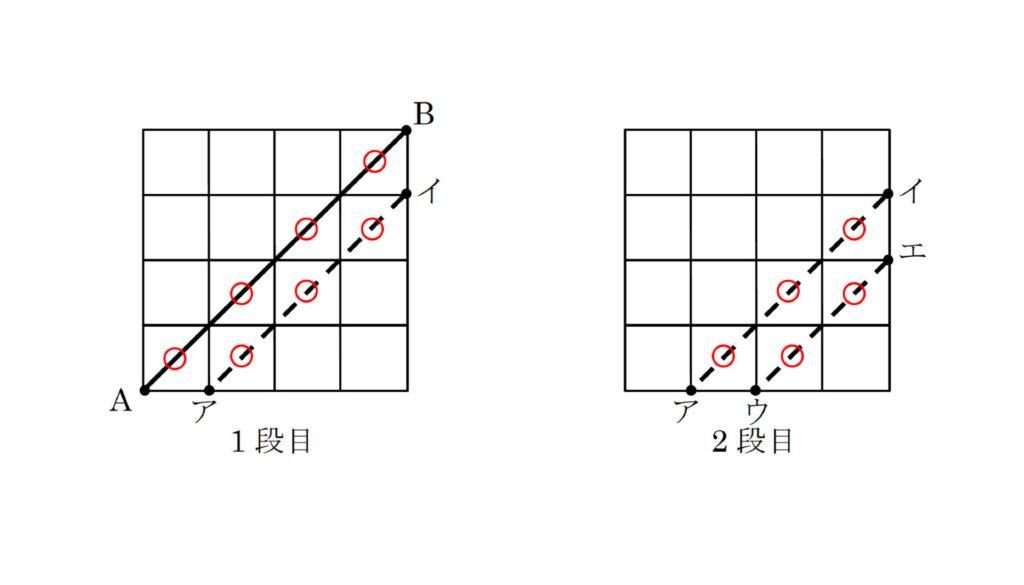
以下のように段ごとに“スライス”してみましょう。1段目ではABが切断の入り口とすると、アイが出口となりますね。「○」のついた7個の小さい立方体が切られたことになります。2段目はアイが入り口、ウエが出口となり、5個の小さい立方体が切られています。3段目、4段目は以下のとおりです。
立体図形の切断を攻略する「手順」――図形問題への取り組み② – 中学受験のアトリエ――中学受験の「いま」を知る
こちらの例題は(i)のパターンで、軸に垂直な平面でスライスしてますね。
過去の公務員試験でも、例題のような「ルービックキューブ状」の立方体が登場していて、そこでもやはり段ごとにスライスするやり方が最適解でした。
ちなみに例題の引用元のサイトには、立方体の切断面を描く手順が紹介されています。
苦手な方は見に行ってみると勉強になるかも。
筆者も「なるほど!」と目からウロコでした。

筆者も受験勉強してたときに知りたかったよ
以上の講義を理解したら、演習問題にチャレンジしましょう!
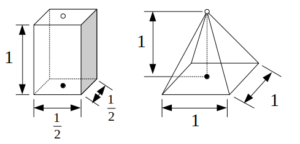
演習問題:直方体と四角すいの共通部分
次図のような直方体および四角すいにおいて、黒点同士、白点同士がそれぞれ重なり合うようにこれら2つの立体を交差させた。このとき、2つの立体の共通部分の体積の最大値はいくらか。
- \(\frac{1}{4}\)
- \(\frac{\sqrt{2}}{4}\)
- \(\frac{1}{6}\)
- \(\frac{\sqrt{2}}{8}\)
- \(\frac{3}{16}\)
3
立体を交差させたときにできる共通部分の体積を求める問題です。
状況を把握するのに適切な図を用意できるかどうかも重要です。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
「最大値」というワードがありますが、ここは素直に、与えられた立体図をそのまま平行移動させたときにできる共通部分の体積を求めるんだ、と考えましょう。
(体積が最大となる場合の議論について、気になる方は「補足」の項を見てください)
実際に重ね合わせてみると次図(左)のようになり、共通部分だけを取り出したものが次図(右)です。

手書きだとちょっとムズカシイ
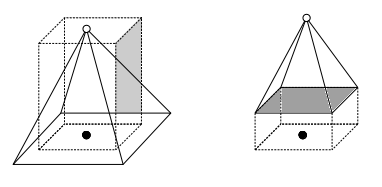
以下、直方体(点線)と四角すい(実線)に分けて体積を求めましょう。
軸を含む切り口で直方体(点線)の体積を考える
直方体(点線)の体積を求めるには、高さを知る必要があります。
ここで「解法のポイント」を思い出しましょう。
適切な切り口を設定しよう
まずは(i)軸に垂直か、あるいは(ii)軸に平行な平面で切ってみるんでしたね。
今回の場合、軸に垂直な切断面を考えてラチが明かないので、軸を含む平面で切ってみます。
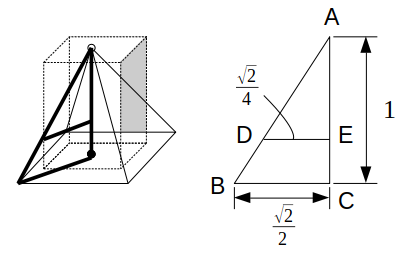
図(左)において太線で示した断面図(右)を考えると、共通部分の直方体の高さはCEの長さにあたります。
BCは1辺の長さが1の正方形の対角線の半分なので、\(\mathrm{BC}=\frac{\sqrt{2}}{2}\)
同様に、\(\mathrm{DE}=\frac{\sqrt{2}}{4}\)
\(\mathrm{BC}:\mathrm{DE}=\mathrm{AC}:\mathrm{AE}\)より、\(\frac{\sqrt{2}}{2}:\frac{\sqrt{2}}{4}=1:\mathrm{AE}\)
これより、\(\mathrm{AE}=\frac{1}{2}\)
よって、直方体(点線)の体積は、\(\left(\frac{1}{2}\right)^2×\frac{1}{2}=\frac{1}{8}\)
四角すい(実線)の体積
底面は1辺の長さが\(\frac{1}{2}\)、高さが\(\frac{1}{2}\)(=AE)の四角すいなので、
\(\frac{1}{3}×\left(\frac{1}{2}\right)^2×\frac{1}{2}=\frac{1}{24}\)
以上より、共通部分の体積は、\(\frac{1}{8}+\frac{1}{24}=\frac{1}{6}\)
よって、3が正解です。
補足:共通部分の体積の最大値?
本問は、重ね合わせた立体の共通部分の体積の「最大値」を求める問題です。
厳密にいうと、解説で示した立体(直方体+四角すい)以外にも、与えられた条件を満足する形が存在します。

軸に関して回転させれば、共通部分の形は無数にあるよ
ここでは、そんな無数のパターンの中から、なぜ解説に示した形が最大であるといえるのかを説明します。
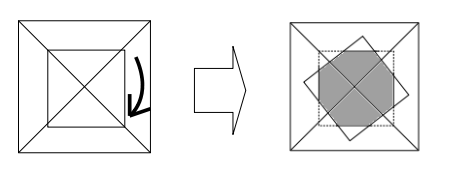
図は重ね合わせた立体を真上から見た様子です。
解説で登場した状態(左)から、直方体を中心軸周りに少し回転させると、共通部分の上半分は四角すいから八角すいに変化します。
高さが一定であることを考えると、体積の大小は底面積の大小によります。
図を見ると、初めの四角形よりも灰色で示した八角形の方が面積は小さいですね。
これにより、共通部分の上半分で比べると、どうしても
(四角すい)>(八角すい)
であることが分かります。
共通部分の下半分については、回転させても体積は変わらないので、上半分の大きさで最大かどうかが決まります。
結局、図(左)のような、四角すいおよび直方体の底面が対角線を共有する場合に、共通部分の体積が最も大きくなるといえます。
つまり、与えられた立体をそのまま平行移動させれば、共通部分の体積を最大とすることができるのです。
おわりに
お疲れ様でした!
いかがだったでしょうか?
空間図形は切り口に注目すると見通しがよくなる場合があります。
2つの立体を重ね合わせてできる共通部分の体積を求める問題でした。
「最大値を求めよ」という書き方は非常に回りくどいですね。
最大とならないケースをあれこれと考え込んで、深みにハマってしまった方もいるかもしれません。
シンプルに、与えられた図を平行移動させればOKです。
重ね合わせたときの共通部分がどんな形なのか、なかなかイメージできなかった方もいるでしょう。
本番では、必要に応じて自分で図を描いて検討しなければならないところに難しさがあります。
空間把握力に優れた方なら、脳内で立体を操作するだけで済んでしまうかもしれませんが……
絵心に自信のある方なら、上手な図を描けるので状況をつかみやすいでしょう。

筆者は空間把握力も絵心も平凡だけど、正八面体くらいまでは手書きできるように練習してたよ
図形の問題は特に、日頃から解説の図を真似て描いてみるなどして、練習しておくのがオススメです。
最後に、「切り口」を扱った問題をもう一問、紹介しておきます。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!次回もお楽しみに!
次回もお楽しみに!
略解
次図(左)のように、底面の対角線がちょうど重なるように置いた場合に共通部分の体積が最大となる。
共通部分だけを抜き出したものが次図(右)である。
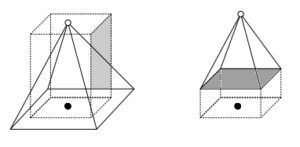
直方体と四角すいの重ね合わせ
以下、共通部分について、下部の直方体と上部の四角すいに分けて体積を求める。
直方体(点線)の体積
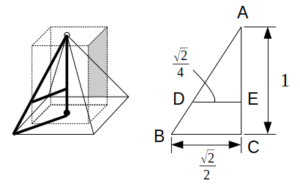
共通部分(直方体)の高さ
図(左)の断面図(右)を考えると、
\(\mathrm{BC}:\mathrm{DE}=\mathrm{AC}:\mathrm{AE}\)より、
\(\mathrm{AE}=\frac{1}{2}\)
よって、直方体(点線)の体積は、
\(\left(\frac{1}{2}\right)^2×\frac{1}{2}=\frac{1}{8}\)
四角すい(実線)の体積
底面は1辺の長さが\(\frac{1}{2}\)、高さが\(\frac{1}{2}\)(=AE)の四角すいであるから、
\(\frac{1}{3}×\left(\frac{1}{2}\right)^2×\frac{1}{2}=\frac{1}{24}\)
以上より、共通部分の体積は、\(\frac{1}{8}+\frac{1}{24}=\frac{1}{6}\)
したがって、3が正解である。

コメント