こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、条件を満たす自然数を数え上げる問題でした。
組合せの考え方を実戦レベルで活用できるか、試すのに丁度よい問題となっています。
ぜひ解いてみてください。
もう解いた方は、お疲れ様でした。
解いた経験をモノにしたいなら、復習は欠かせません。
復習するときは、解法のエッセンスを見つけ出すことを意識してみてください。
個々の解説から、他の問題にも応用可能な要素を抽出して学習する、ということです。
本試験で過去問と全く同じ問題が出ることはありませんが、似たような問題ならば出る可能性はあります。
だからこそ、学習した解法を一般化してストックしておくことが必要となります。
本サイトでは「解法のポイント」としてまとめているものもあるので、ぜひご活用ください!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
図1のような壁に囲まれた格子点上を、サイコロの出目に応じて移動する駒Aを考える。駒Aには向きがあり、進行方向が分かるようになっている。いま、図1の状態から始めて、点Pが隣接する格子点に移動するごとにサイコロを1回振り、出た目の数に応じて駒Aを移動させる、という試行を繰り返す。
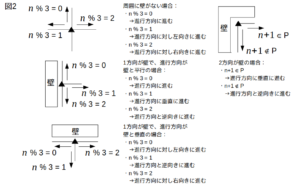
移動の規則を図2に示す。ただし、サイコロの出目\(n\)に対し、「\(n\)%3」は\(n\)を3で割った余りを、「\(n\)∈P」は\(n\)が素数であることを、それぞれ表すものとする。
このとき、4回の試行の後に駒Aが点Bにある確率はいくらか。

- \(\frac{4}{81}\)
- \(\frac{2}{27}\)
- \(\frac{1}{9}\)
- \(\frac{4}{27}\)
- \(\frac{14}{81}\)
4
サイコロの出目に応じて駒を動かす問題です。
設定がやや複雑ですが、まずはきちんと問題文を読んで頭に入れてください。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
求める確率は、4回の移動で点Bにたどり着く確率です。
これは、スタート地点から最短経路を通って点Bにたどり着く確率のことです。
最短経路は、全部で\({}_4 \mathrm{C}_2=6\)通りあります。
たかだか6通りなら、総当りしてもさほど時間はかからないでしょう。
各格子点を右図のように区別し、6通りの経路を以下に列挙します。
(i)S→C→D→G→B
(ii)S→C→F→G→B
(iii)S→C→F→I→B
(iv)S→E→F→G→B
(v)S→E→F→I→B
(vi)S→E→H→I→B
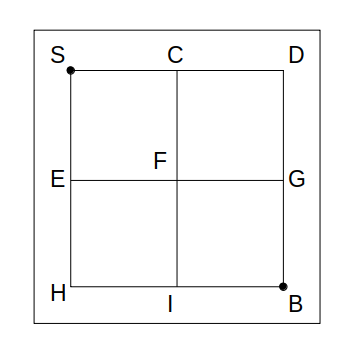
本問では、駒Aが壁に接するか否かによって状況が変わるので、最短経路を選ぶ確率を1ステップずつ確かめて乗じていく必要があります。
(i)S→C→D→G→Bの場合
S→Cと移動するのは、「\(n+1\)∈P」が成り立つとき、すなわちサイコロの出目が1、2、4、6のときなので、確率は\(\frac{2}{3}\)
C→Dと移動するのは、「\(n\)%3=0」のとき、すなわち出目が3、6のときなので、確率は\(\frac{1}{3}\)
D→Gと移動するのは、「\(n+1\)∈P」が成り立つときなので、確率は\(\frac{2}{3}\)
G→Bと移動するのは、「\(n\)%3=0」のときなので、確率は\(\frac{1}{3}\)
以上より、S→C→D→G→Bの経路で進む確率は、\(\frac{2}{3}×\frac{1}{3}×\frac{2}{3}×\frac{1}{3}=\frac{4}{81}\)
以下、同様にして(ii)〜(vi)における確率を求めます。
(ii)S→C→F→G→Bの場合
\(\frac{2}{3}×\frac{1}{3}×\frac{1}{3}×\frac{1}{3}=\frac{2}{81}\)
(iii)S→C→F→I→Bの場合
\(\frac{2}{3}×\frac{1}{3}×\frac{1}{3}×\frac{1}{3}=\frac{2}{81}\)
(iv)S→E→F→G→Bの場合
\(\frac{1}{3}×\frac{1}{3}×\frac{1}{3}×\frac{1}{3}=\frac{1}{81}\)
(v)S→E→F→I→Bの場合
\(\frac{1}{3}×\frac{1}{3}×\frac{1}{3}×\frac{1}{3}=\frac{1}{81}\)
(vi)S→E→H→I→Bの場合
\(\frac{1}{3}×\frac{1}{3}×\frac{2}{3}×\frac{1}{3}=\frac{2}{81}\)
(i)〜(vi)のケースは全て独立なので、求める確率は
\(\frac{4}{81}+\frac{2}{81}+\frac{2}{81}+\frac{1}{81}+\frac{1}{81}+\frac{2}{81}=\frac{4}{27}\)
よって、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
最短ルートで駒がゴールにたどり着く確率を求める問題でした。
駒が壁に接するか否か、および壁と進行方向との関係によって状況が変わるため、1ステップずつ確率を調べて乗じる必要があります。
「\(n\)%3」や「\(n+1\)∈P」といった条件を、確率に読み替えるのはさほど難しくないでしょう。
駒の位置と向きを丁寧に追って、正しい選択肢を選びましょう。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
スタート地点から最短経路(\({}_4 \mathrm{C}_2=6\)通り)を通って点Bにたどり着く確率を求めればよい。
各格子点を次図のように区別し、最短経路を以下に列挙する。
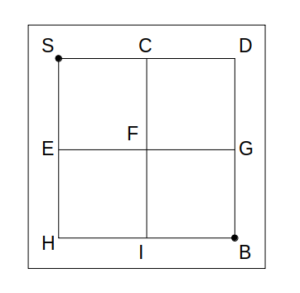
格子点をアルファベットで区別
(i)S→C→D→G→B
(ii)S→C→F→G→B
(iii)S→C→F→I→B
(iv)S→E→F→G→B
(v)S→E→F→I→B
(vi)S→E→H→I→B
各経路について、1ステップごとに次の点に移動する確率を求め、乗じることでそれぞれの確率を求める。
(i)S→C→D→G→Bの場合
\(\frac{2}{3}×\frac{1}{3}×\frac{2}{3}×\frac{1}{3}=\frac{4}{81}\)
(ii)S→C→F→G→Bの場合
\(\frac{2}{3}×\frac{1}{3}×\frac{1}{3}×\frac{1}{3}=\frac{2}{81}\)
(iii)S→C→F→I→Bの場合
\(\frac{2}{3}×\frac{1}{3}×\frac{1}{3}×\frac{1}{3}=\frac{2}{81}\)
(iv)S→E→F→G→Bの場合
\(\frac{1}{3}×\frac{1}{3}×\frac{1}{3}×\frac{1}{3}=\frac{1}{81}\)
(v)S→E→F→I→Bの場合
\(\frac{1}{3}×\frac{1}{3}×\frac{1}{3}×\frac{1}{3}=\frac{1}{81}\)
(vi)S→E→H→I→Bの場合
\(\frac{1}{3}×\frac{1}{3}×\frac{2}{3}×\frac{1}{3}=\frac{2}{81}\)
以上、(i)〜(vi)は全て独立だから、求める確率は
\(\frac{4}{81}+\frac{2}{81}+\frac{2}{81}+\frac{1}{81}+\frac{1}{81}+\frac{2}{81}=\frac{4}{27}\)
したがって、4が正解である。


コメント