こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本ブログ、「数的処理の穴場」を運営しておりますモクセイと申します。
今回のテーマは「面積」です。
実は、面積の問題の解法って2パターンしかないんです。
以下の記事に詳しく書いているので、まだ見てない方はぜひ覗いてみてください。

まだの方は先に見てきてもらえると理解が早いかも
演習問題:図形の折り返しと面積
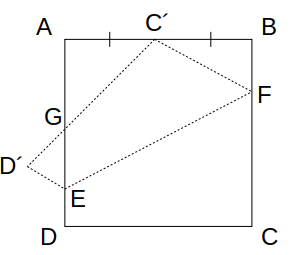
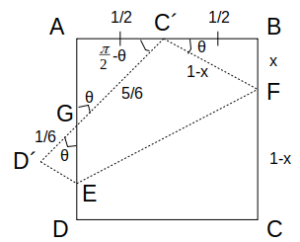
1辺の長さが1である正方形ABCDにおいて、図の線分EFを折り目として、頂点Cが辺ABの中点に重なるように折り返すことを考える。
折り返したときの頂点Cおよび頂点Dの移る先をそれぞれC´、D´とし、ADとC´D´の交点をGとするとき、三角形D´EGの面積はいくらか。
- \(\frac{1}{8}\)
- \(\frac{3}{13}\)
- \(\frac{\sqrt{3}}{56}\)
- \(\frac{1}{96}\)
- \(\frac{\sqrt{3}}{32}\)
4
折り返しがテーマの図形問題です。
「中点」という条件が提示されていることから、線分の長さがカギになってきそうですね。
以下、詳しい解説ですが、回りくどいのが苦手な方は一番下に略解も載せてあるので、そこだけ見てもらっても大丈夫です。
それでは、解説スタート!
詳しい解説
図形問題で面積を求める方法は、大きく分けて2つ。
- 大きさが分かっている図形との相似比から求める方法
- 具体的に長さを求めて面積公式に当てはめる方法
1は相似比などを利用して解く方法なので、「角度」とか「平行線」が問題の条件として与えられることが多いです。
対して、2は長さに関する情報が与えられた場合に有効です。
本問では「1辺の長さが1」とか「中点」といったヒントがあるので、2の方針が使えそうですね。
必要なのは直角三角形D´EGの2辺D´EおよびD´Gの長さです。
以下、直角三角形D´EGの2辺D´EおよびD´Gの長さを求める方針で進めます。

直角三角形に注目するのがポイント
直角三角形BC´Fの辺の長さ
辺BFの長さを\(x\)とおくと、BCは正方形の1辺なので、線分CFの長さは\(1-x\)です。
ここで、折り返し、という条件を思い出しましょう。
もともと、線分C´Fは線分CFを折り返したものなので、長さは一致します。
よって、線分C´Fの長さも\(1-x\)です。
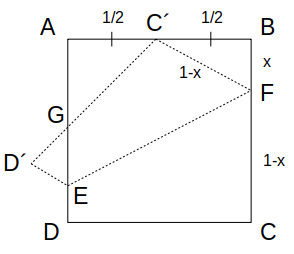
これで直角三角形BC´Fの3辺の長さが出揃いましたね。
三平方の定理を使えば、\(x\)の値を求めることができます。
\((1-x)^2=x^2+(\frac{1}{2})^2\)を解いて、\(x=\frac{3}{8}\)

二次方程式に見えるけど、整理してみると一次方程式になるよ
直角三角形AC´Gの辺の長さ
直角三角形AC´Gについて、与えられた条件だけでは辺AC´が\(\frac{1}{2}\)であることしか分かりません。
辺C´Gの長さが分かれば、C´D´=1よりD´Gが分かるのですが、何かいい方法はないでしょうか?
結論を言うと、三角比を使います。
△AC´Gは直角三角形なので、∠AC´G(あるいは∠AGC´)が分かれば三角比が利用できそうですね。
∠BC´F=\(\theta\)とおけば、∠BC´F+∠FC´D+∠AC´G=\(\pi\)より、∠AC´G=\(\frac{\pi}{2}-\theta\)となります。

∠AGC´=∠D´GE=\(\theta\)となることも分かるね
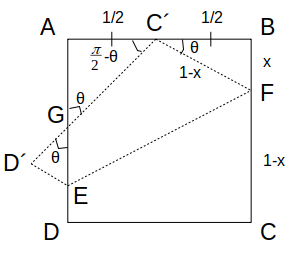
このとき、角度\(\theta\)に関する三角比が以下のように求められます。
\[
\sin\theta=\frac{\mathrm{BF}}{\mathrm{C´F}}=\frac{3}{5},
\cos\theta=\frac{\mathrm{BC´}}{\mathrm{C´F}}=\frac{4}{5},
\tan\theta=\frac{\mathrm{BF}}{\mathrm{BC´}}=\frac{3}{4}
\]
これを用い、直角三角形AC´Gの辺の長さC´Gを以下のように求めます。
\[
\mathrm{C´G}=\frac{\mathrm{AC´}}{\cos(\frac{\pi}{2}-\theta)}=\frac{\frac{1}{2}}{\sin\theta}=\frac{5}{6}
\]

補角や半角の公式を使ってるよ
この辺りの計算がやや複雑なので注意
直角三角形D´EGの辺の長さと面積
すると、\(\mathrm{D´G}=\mathrm{C´D´}-\mathrm{C´G}=\frac{1}{6}\)のようにD´Gの長さも分かります。
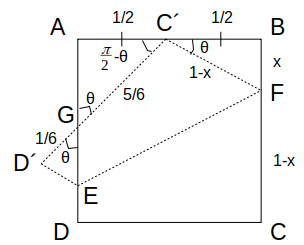
さらに、∠D´GE=\(\theta\)の関係、および△D´EGが直角三角形であることより、以下のように辺D´Eの長さを求めます。
\[
\mathrm{D´E}=\mathrm{D´G}\tan\theta=\frac{1}{8}
\]
これで、直角三角形D´EGの2辺D´G(底辺)およびD´E(高さ)が揃いましたね。
あとはこれらを面積公式に当てはめればいいですね。
\[
△\mathrm{D´EG}=\frac{1}{2}\mathrm{D´G}×\mathrm{D´E}=\frac{1}{2}×\frac{1}{6}×\frac{1}{8}=\frac{1}{96}
\]
したがって、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
面積の問題は、相似比か面積公式で解けます。
折り返しという条件と、長さや角度の設定がポイントとなる問題でしたね。
途中、「余角の公式」と「半角の公式」を利用してます。
しれっと使っていますが、余角の公式も併せて、三角比(三角関数)の公式はしっかりと使えるように頭の引き出しに入れておいてください。
国家総合職の数的処理を攻略する上で、平面図形の対策は避けて通れません。
平面図形の対策を怠ると空間図形の問題も苦しくなりますから、くれぐれも万全の対策をとって本番に臨んでほしいと思います。

空間図形も毎年1〜2問出題されてるね
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、
ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解

線分BFをxとおく
直角三角形BC´Fにおいて、\((1-x)^2=x^2+(\frac{1}{2})^2\)より、\(x=\frac{3}{8}\)
また、∠BC´F=\(\theta\)とおくと、∠BC´F+∠FC´D+∠AC´G=\(\pi\)より、∠AC´G=\(\frac{\pi}{2}-\theta\)
すると、直角三角形AC´Gにおいて、∠AGC´=∠D´GE=\(\theta\)

角度θの設定
直角三角形BC´Fにおいて
\[
\sin\theta=\frac{\mathrm{BF}}{\mathrm{C´F}}=\frac{3}{5},
\cos\theta=\frac{\mathrm{BC´}}{\mathrm{C´F}}=\frac{4}{5},
\tan\theta=\frac{\mathrm{BF}}{\mathrm{BC´}}=\frac{3}{4}
\]
これを用いると、直角三角形AC´Gについて、
\[
\mathrm{C´G}=\frac{\mathrm{AC´}}{\cos(\frac{\pi}{2}-\theta)}=\frac{\frac{1}{2}}{\sin\theta}=\frac{5}{6}
\]
ゆえに、\(\mathrm{D´G}=\mathrm{C´D´}-\mathrm{C´G}=\frac{1}{6}\)
D´Gの長さの算出
したがって、
\[
△\mathrm{D´EG}=\frac{1}{2}\mathrm{D´G}×\mathrm{D´E}=\frac{1}{2}\mathrm{D´G}×\mathrm{D´G}\tan\theta=\frac{1}{96}
\]
よって、正解は4である。

コメント