こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本ブログ、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、いくつかの条件と順序関係から座席の位置を確定させる問題をやりましたね。
本日は第四回目!早速問題文を見ていきましょう。
本日の演習問題
ただし、2名以上が同時に控室を出ることも、2名以上が同時に控室に戻ってくることもなかったものとする。
- 控室に戻ったときに部屋にいた人数が、自分を除いて3人だったという人は2人いて、自分を除いて2人いたという人、および1人いたという人はそれぞれ1人いた。
- 控室を出たときに自分を除いて部屋にいた人数と、戻ったときに自分を除いて控室にいた人数が同じだった人は1人だった。
- 控室を出たときに自分を除いて部屋に2人いたという人は、2番目に戻ってきた人ではない。
- Dが控室を出たとき、部屋には自分を除いて1人いた。
- Aは2番目に控室に戻ってきた。
- Bは3番目に戻ってきた。
- Cは1番最後に戻ってきた。
- Dは1番最初に戻ってきた。
- 控室に誰もいないという状況があった。
3
順序関係の問題です。4つの条件から、A〜Dが控室を出たときと戻ってきたときの人数と、控室に戻ってきた順序を検討します。
以下に詳しい解説を載せますが、回りくどいのが苦手な方は一番下の略解だけ見る、でも大丈夫です。
それではスタート!
詳しい解説
最終的には4つの条件ア〜エの全てを満たす状況を考えなくてはならないので、いっそ始めから1つの条件を満たす状況を全て列挙してしまい、それらのうちから他の条件を満たさないものを省いていく、という手順でいきましょう。
これだけだと、さすがにどういうことか分かりませんね汗
具体的には、まず条件アの前半、「控室に戻ったときに部屋にいた人数が、自分を除いて3人だったという人は2人」という箇所に注目します。
最初から「控室に戻ったときに〜」という条件を認めてしまい、これを満たす場合を全て洗い出してしまうんです。
「控室に戻ったときに〜」の2人が出ていった後の状況の変化を考えると、次の3通りの場合が挙げられます。
- 2人とも、自分が出た後に誰も控室を出ないうちに戻ってきた。
- 2人とも、自分が出た後に控室を出た人が少なくとも1人いた。
- 2人のうち1人が、自分が出た後に誰も控室を出ないうちに戻ってきた。
イの場合、代表として次の表1および表2のような変化のし方がありますが、いずれも条件エの「控室を出たとき、部屋には自分を除いて1人いた」という部分を満たすことができないので、イは間違いです。(ちなみに、1人減るタイミングが前半ではなく後半だった可能性もありますが、どのみち条件エを満たしません。)
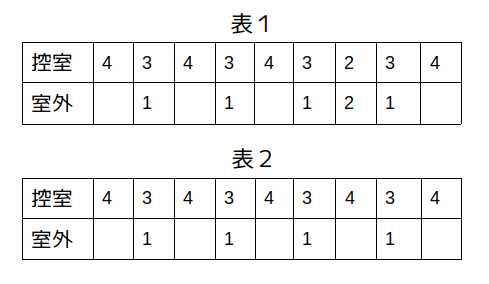
ロの場合は次の表3のような変化のし方が考えられますが、やはり条件エの「部屋には自分を除いて1人いた」という箇所に合いません。
よって、ロも間違いとなります。
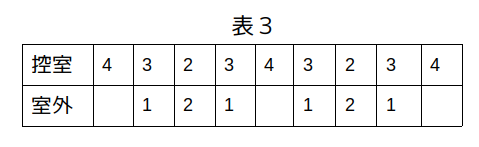
続くハの場合はさらに分岐します。
つまり、「自分が出た後に誰も控室を出ないうちに戻ってきた」が起こるタイミングが最初か、あるいは最後かによって次の表4、表5の2通りに枝分かれします。
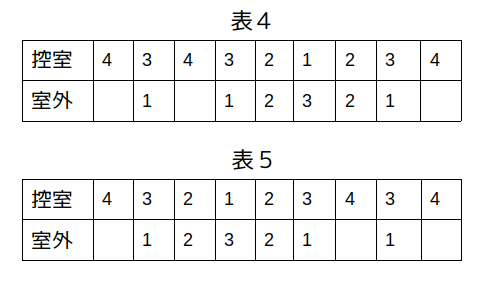
条件エによると、Dが控室を出るときの残りの人数は1人でなければならないので、最後の1人が控室を出るときの残り人数が3人である表5は候補から外れます。
以上から、条件を満たしうるのは表4に示す場合のみ、ということになります。
(この時点で選択肢5は不正解であると分かります。)
あとは表4に従ってA〜Dの4人の動きを確定させるだけです。
まず、「控室を出たときに自分を除いて部屋にいた人数と、戻ったときに自分を除いて控室にいた人数が同じだった」1人を確定させます。
表4を見ると、それはAだと分かります(控室を出たときと、戻ってきたときの人数がともに3人)。
次に、2番目に戻ってきた人は誰なのかを考えましょう。
表4によると、2番目に人が戻ってきたときの控室には、最初に戻ってきたAのみがいます。
条件エより、Dが戻ってきたとき「部屋には自分を除いて1人いた」ので、2番目に戻ってきたのはDでなければなりません。
この時点で、控室にはAとDがいて、戻ってきていないのはBとCです。
この後、BとCが順に戻ってくるわけですが、どちらが先でしょうか?
答えは条件イから確定させることができます。
つまり、今控室にいるのは2人なので、控室を出たときの残り人数が「2人ではなかった」人が3番目です。
表4によると、それはBだと分かりますね。
残る4番目はCと決まります。
控室に戻ってきた順番はA→D→B→Cでした。
出入りの状況をまとめると、表6のようになります。
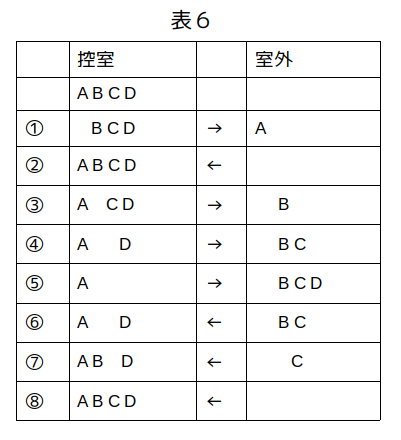
逆算的に表6から条件ア〜エを検討しても矛盾はありません。
したがって、正解は3となります。
おわりに
お疲れ様でした!
いかがだったでしょうか?
問題だけ見ると捉えどころのないように思われますが、1つの条件を足がかりに場合分けすることで少しずつ状況を絞り込んでいくことができました。
条件から逆算する方法もあるのだ、と知っていただければ、私も出題した甲斐があります。
国家総合職の数的処理は、例えば「位置関係」や「順序関係」というありきたりなテーマであっても、設定が複雑なものや、分野横断型の複合的な問題が頻繁に出題されています。
今回でいえば、4人が控室を出た順番だけでなく戻ってきた順番も明らかにしなければならないところが、この問題の複雑さの所以となっていたと思います。
こうした問題への対策としては、月並みですが基礎と言われるレベルの問題を確実に理解することに尽きます。
設定が複雑な問題も、元をただせば基礎問題の解き方に帰着する場合がきわめて多いですし、設定がシンプルな問題の理解なくしては複雑な問題の理解は難しいからです。
今回の問題で正しい解法に至らなかったという方は、最初に勉強した参考書で「順序関係」を扱った問題を復習してみるのもおすすめです。
本ブログでは、今後もこうした演習用の問題をアップしていく予定なので、
ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
という部分について、この2人が控室を出た後の部屋の人数の変化によって、以下の3通りに場合分けできる。
- 2人とも、自分が出た後に誰も控室を出ないうちに戻ってきた。
- 2人とも、自分が出た後に控室を出た人が少なくとも1人いた。
- 2人のうち1人が、自分が出た後に誰も控室を出ないうちに戻ってきた。
イの場合、表1および表2の状況がありうるが、いずれも条件エを満たせないので不適。
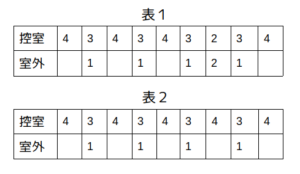
4→3→4の変化が2回ある場合
ロの場合、表3のような状況がありうるが、やはり条件エを満たせないので不適。
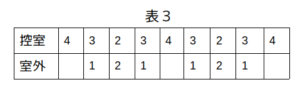
4→3→2→3の変化が2回のとき
ハの場合は、「自分が出た後に誰も控室を出ないうちに戻ってきた」という状況が起こったタイミングによって、さらに表4、表5に示す2つのパターンに分岐する。
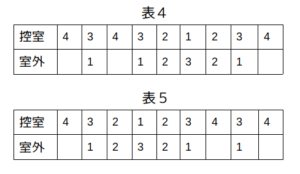
4→3→4の変化が1回のとき
しかし、表5は条件エを満たさないため不適。
つまり、この問題では表4の場合だけ考察すればよいことになる。
この場合、まず条件イを満たすのは、表4より最初に控室を出る人、すなわちAである。
次に、2番目に戻ってくる人は誰かを考える。
表4を見ると、2番目に人が戻ってくるとき、控室にはAのみがいる状況だったと分かる。
条件エより、それはDでなければならない。
同時に、条件イはDのことを述べた文章であったと分かる。
すると、3番目と4番目に戻ってくるのはそれぞれB、Cと決まる。
(B→出るとき3人だったので戻ったとき2人である必要があるから)
4人の出入り状況を表6としてまとめる。
表6は条件ア〜エを全て満たしているので、これは正しい。
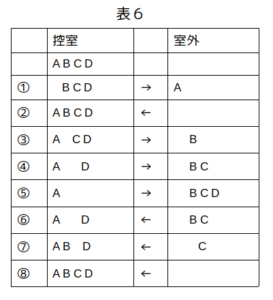
控室の出入り状況まとめ
よって、正解は3である。

コメント