こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
「貧乏な人の特徴」という本にある、「貧乏な人は学歴が資産形成につながると思い込む」という指摘にはハッとさせられました。
学生時代はテストで点数を取ることが一つのステータスなので、その延長で勉強をがんばれば社会でも通用する、とつい思ってしまいますよね。
このサイトに来る方は、今、国家総合職を目指して数的処理を勉強しているかと思いますが、高得点を取ったあとの「それから先のこと」もぜひ思い描いてみてほしいと思います。
二次試験には面接もありますし、何よりその先には官庁訪問も待ってますからね。
前回は、展示会で1日に訪問できるブースの最大数を求める問題をやりましたね。
解法のポイントは覚えていますか?
大まかでもいいので、どんな問題で、どんな解き方だったか、この場で思い出してみましょう。
思い出すことで、記憶が強化されていきます。
完全に忘れてしまう前に思い出すことを習慣化しましょう。
このやり方は数的処理以外の科目にも使えるのでおすすめです!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
A、B、C、D、Eと書かれた箱が左からアルファベット順に並んでいる。いま、Aの箱には黒球を、B〜Eの箱には白球をそれぞれ1つずつ入れ、次の操作を任意の順序で何回か行って箱の中身を入れ替えることを考える。
- A〜Eのうちからランダムに2つの箱を選び出し、互いの中身を入れ替える。
- A〜Eのうちから箱をランダムに1つ選び、中身の色を反転させる(選んだ箱の中身が黒球なら代わりに白球を入れ、箱の中身が白球であったら代わりに黒球を入れる)。
- 箱の中身を次のアルファベットの箱へ移す。ただし、Eの箱の中身はAの箱に移す。
これらの操作を合計で5回行ったところ、B、C、Eの箱の中身が黒球で、A、Dの箱の中身が白球であった。このとき、確実にいえるのはどれか。
- αは少なくとも1回は行われた。
- βを行った回数は、αを行った回数よりも多い。
- βを行った回数は2回または3回または4回である。
- γが2回行われたとすれば、その2回は連続している。
- γは1回も行われなかった可能性がある。
5
始まりと終わりの状態が決まっている中で、途中どのような操作が行われたかを推測する問題ですね。
始めの状態から出発して、矛盾なく終わる操作手順にはどんなものがあるか、検討しましょう。
以下で詳しく解説します。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただいても問題ありません。
それではスタート!
詳しい解説
条件に合う操作手順としては、例えば「ααγββ」があります。
(=最初の2回のαでそれぞれBとC、DとEが選ばれ、最後の2回のβでCとEが選ばれればよい)
このように、実現可能な操作手順を挙げていくのも解決法の一つですが、これには問題点があります。
- 一つの組み合わせの中に可能な手順が何通りもある(αβγαβもあり得る)
- 「ααγββ」の手順一つに対して箱の選び方が何通りもある(最初の2回のαで2回ともCとDが選ばれる場合もあり得る)
手順も箱の選び方もただ一つに定まるような場合なら、可能な手順を全て列挙するやり方もアリですが、本問にはあまり有効ではなさそうです。
では、どうするか。
以前の記事で、選択肢から逆算する考え方の有用性をお伝えしました。
この考え方を本問に応用すると、例えば1の「αは少なくとも1回は行われた」だったら、αが1回も行われなかった場合、つまりβとγだけで条件を満たせるかを考えればいいですね。
(βとγだけで条件を満たせるなら、1は誤りであると分かります)
検証してみましょう。
1について
例えば、最初にBとDにβを行ってから、次にγを行うと、3回の操作で「B、C、Eの箱の中身が黒球で、A、Dの箱の中身が白球」という状況になります。
あとは残りの2回で、どれでもいいので一つの箱(Aとします)にβを2回適用してやると、そのまま条件を満たします。
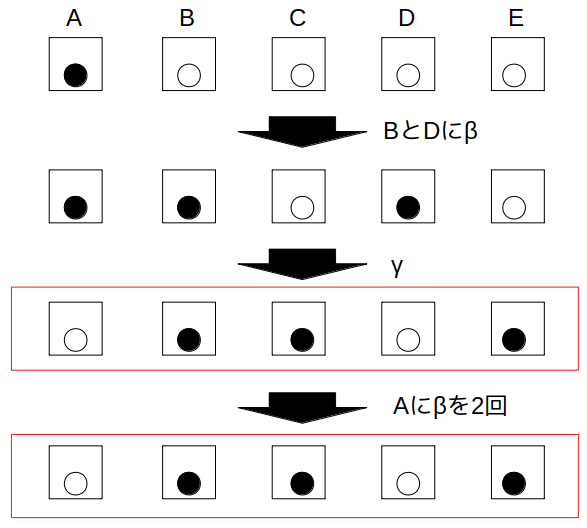
このようにすれば、αを行わずとも条件を満たすことができるので、1は誤りです。
2以降も同じように、反例を探す方針で検証していきましょう。
2について
ここでいう「反例」とは、次のような場合です。
(αの回数)>(βの回数)・・・(☆)
3種類の操作のうち、黒球の数を増やすことができるのはβしかありません。
始めは1つしかなかった黒球が、終了時には3個にまで増えていることを考えると、5回の操作のうち、少なくとも2回はβが行われる必要があります。
その中で、☆印の状況が起こるとすれば、それは「αが3回、βが2回」行われたときしかありません。
そのような操作のし方があれば、2は誤りだといえますね。
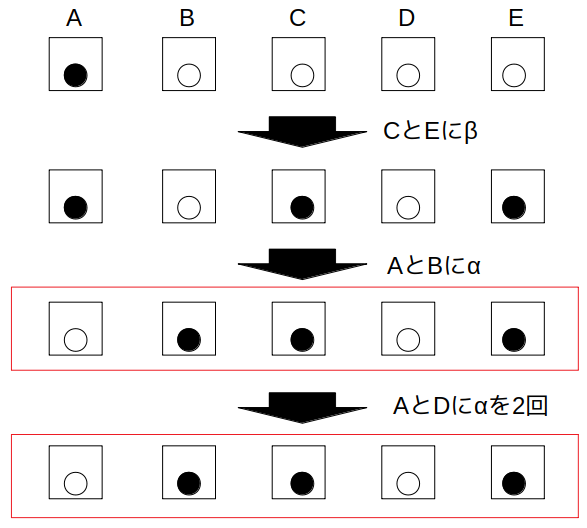
例えば、終了時にはCとEに黒球が入っていることより、最初の2回でCとEにβが行われたと考えます。
次にAとBに対しαが行われると、この時点で条件を満たすことが可能です。
あとは同じ色の箱同士(例えばAとD)でαが2回行われれば、「αが3回、βが2回」で条件を満たすことが可能となります。
よって、☆印を満たすような操作手順が可能なため、2は誤りとなります。
3について
前項で、βは少なくとも2回行われる必要があることを述べました。
これが3回になると、黒球は1つ増えて4つか、1つ減って2つか、のいずれかになります。
いずれにせよ、これでは「B、C、Eの箱の中身が黒球」という状況にはなり得ません。
したがって、βが3回という手順はあり得ないので、3は誤りとなります。
ちなみに、βが4回のときは、最低回数の2回で黒球を3個にしたあと、残り2回は同じ箱を選べば黒球は3個のままなので、条件を満たす操作が可能です(例えば、ββββα)
4について
2回のγが連続しないような手順があるか?を考えればいいですね。
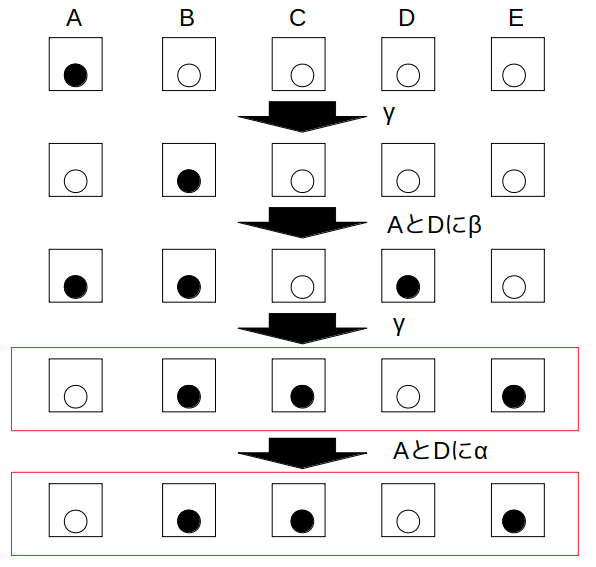
まずγを1回行って、Aにある黒球をBに移します。(白黒白白白)
次に、AとDにβを行ったあと(黒黒白黒白)、γを1回行うと最終的な形(白黒黒白黒)となります。
あとは最後の1回で同じ中身の箱同士にαを行えば(例えばAとD)、条件を満たします。
この場合はγを2回行っているにもかかわらず、それらは連続していないので、4は誤りです。
※この時点で消去法により5が正解と分かってしまいますが、念のため5も解説します。
5について
この場合、反例を考えるとややこしいので、素直にγが1回もないケースはあり得るか?を考えます。
まず、αを4回、AとBとCとEに行うと、最終的な形になります。
あとは、最後の1回で中身が同じ箱(例えばAとD)に対してβを行えば、そのまま条件を満たします。
よって、γが1回も行われない手順は可能なので、5は正しい。
以上より、5が正解となります。
おわりに
お疲れ様でした!
いかがだったでしょうか?
判断推理では、あり得るケースを全て洗い出す、というのはありがちな解法ですが、本問でそれは得策とはいえません。
解説したように、選択肢を利用して「反例」を探していく方が近道です。
反例を探すときは、条件の範囲内でできる限り簡単な手順を見つけるのがコツになります。
例えば、最後の5なんかは、αのゴリ押しで条件を満たす形(白黒黒白黒)を作り出したあと、最後にβで当たり障りのない(=状況を変化させない)箱を選んでます。
この場合はあくまで「γが1回もない」というのが前提条件なので、それさえ守ればあとは好きに考えていいんです。
国家総合職の数的処理としては、本問のような操作手順を題材にした問題は多くはありませんが、割と近年にも出題された実績はあるので、今後また登場する可能性は十分にあると考えられます。
参考書で学んだ基礎を活用することができるのかどうかを確かめるには、過去問を解いてみるのが一番です。
このサイトで扱う問題は過去問に準じたレベルになっているので、この記事を最後まで読んでくれたあなたは、国家総合職レベルの操作手順の問題に対応する力が確実にアップしています。
参考書を一通り終えた後のトレーニングとして、ぜひ本サイトを活用していただければと思います!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
1:×
例えば、最初にBとDにβを行ってから、次にγを行うと、3回の操作で目的の状況(白黒黒白黒)になる。
残りの2回で、任意の一つの箱(Aとする)にβを2回適用すると、そのまま条件を満たす。
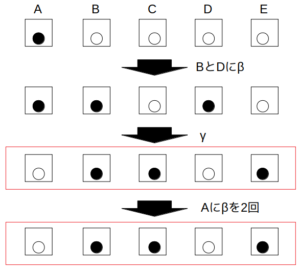
αを用いずに条件を満たす手順
このように、αを行わずに目的の状況に至ることが可能なので、1は誤りである。
(αの回数)>(βの回数)・・・(☆)を満たす操作手順があり得るのかを考えればよい。
ここで、始めは1つだった黒球が、終了時には3個に増えていることより、少なくとも2回はβが行われたことになる。
よって☆印の状況が起こるとすれば、それは「αが3回、βが2回」行われたときしかない。
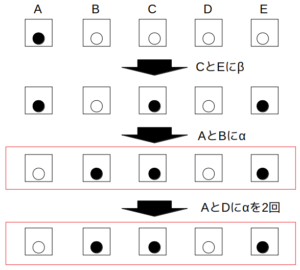
例えば、最初の2回でCとEにβが行われたときを考える。(黒白黒白黒)
次にAとBに対しαが行われると、目的の状況(白黒黒白黒)になる。
あとは同じ色の箱同士(例えばAとD)でαが2回行われれば、「αが3回、βが2回」で目的の状況が実現できる。
よって☆印を満たすケースがあり得るので、2は誤りである。
3:×
前項の通り、βは少なくとも2回行われる必要がある。
これが3回になると、黒球は1つ増えて4つか、1つ減って2つか、のいずれかになるため、目的の状況は実現し得ない。
したがって、βが3回行われるような手順はあり得ないので、3は誤りである。
なお、βが4回のときは、白球の箱にそれぞれβを行って黒球を3個に増やしたあと、残り2回は同じ箱を選べば黒球は3個のままとなるので、目的の状況を実現できる(例えば、ββββαなど)
4:×
2回のγが連続しないような手順があるかを考える。
まずγを1回行う。(白黒白白白)
次に、AとDにβを行い(黒黒白黒白)、そこにγを1回行うと目的の状況(白黒黒白黒)となる。
最後の1回で同じ中身の箱同士(例えばAとD)にαを行えば、目的の状況が実現できる。
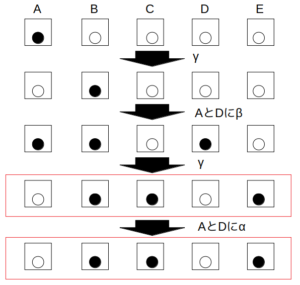
2回のγが連続しない手順
よって、2回のγが連続しない手順があり得るので、4は誤りである。
5:○
反例を考えるとややこしいので、γが1回もないケースはあり得るかどうかを考える。
まず、αを4回、AとBとCとEに行うと、目的の形となる。
最後の1回で中身が同じ箱(例えばAとD)に対してβを行えば、目的の状況が実現される。
よって、γが1回もない手順があり得るので、5は正しい。
以上から、正解は5である。

コメント