こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
新しくインストールしたスマホゲーが開始早々に落ちるので未だに始められない。
数年前に回線契約の割引対象だった機種なので、そろそろ型落ちでしょうかね。
買い替えるにしたところで、他に欲しい機種って特にないんだよなー。
機種変するなら回線も乗り換えたいので、割引キャンペーンを活用したいところですが、そうなるとますます選択肢が限られる……
まあ、あまり焦らないで決めようと思います。
前回は、直方体と四角すいが共有する領域の体積を求める問題をやりましたね。
国家総合職で毎年のように出題がある空間図形の問題です。
まだ問題を見てない方はぜひ挑戦してみてください。
解き終わった方も、しっかり復習して知識を定着させることが大切です。
一度解いただけでは、まだ安心できません。
解説を読んで理解したつもりでも、いざ自力で解いてみると思うように進まなかった、ということはよく起こります。
ここで手が止まったり間違えたりした箇所は、再度解説を読み直してきちんと納得しておくことが必要です。
問題演習で、ただ一度だけ解いて満足してしまうのはもったいないです。
数をこなすだけでなく、学んだ解法を一つずつ身につけることにも気を配ってみてください。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
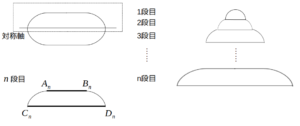
角丸長方形とは、二つの半円が平行な線分によってつながれた図形で、陸上競技のトラックによく用いられる。この角丸長方形を次図に示す対称軸で分割し、次に示すルールに従って積み重ねることでできる段組み図形を考える。
ルール1:段組み図形の最頂部は半径\(r\)の半円とすること。
ルール2:\(\mathrm{C}_n\mathrm{D}_n=\mathrm{A}_{n+1}\mathrm{B}_{n+1}\)であること。
このとき、\(n=60\)における段組み図形の外周の長さとして正しいのは、次のうちどれか。
- \(30\pi r\)
- \(60(\pi+1)r\)
- \(60(\pi+2)r\)
- \(120(\pi+1)r\)
- \(120(\pi+2)r\)
3
半角丸長方形を積み重ねる問題です。
「ルール」と与えられた図がヒントです。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
念のため確認すると、「外周の長さ」とは次図の太線のことです。
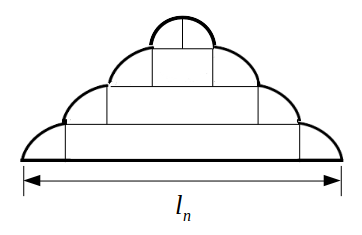
図のように補助線を加え、各段を長方形と扇形に分割すると見通しが良くなります。
これによると、\(n\)段の場合は\(2×n\)個の四半分の扇形(=\(n\)個の半円)と、長さ\(l_n\)の線分からなることが分かります。
長さについて、前者は\(n\pi r\)として、後者はどうやって求めたらよいでしょう?
ここも、やはり補助線を用いた分割に着目しましょう。
再三になりますが、\(n\)段目は長方形と四半分の扇形2つ(=半径\(r\)の半円1つ)に分けられます。
長さでいうと、前者は\(l_{n-1}\)、後者は\(2r\)ですね。
式にすると、\(l_n=l_{n-1}+2r\)
すなわち、\(l_n-l_{n-1}=2r\)
両辺を、区間\(2≦n≦60\)で和をとると、\(l_{60}-l_1=59×2r=118r\)
\(l_1=2r\)であったことを思い出すと、\(l_{60}=118r+l_1=120r\)
ゆえに、\((外周の長さ)=60\pi r+l_{60}=60(\pi+2)r\)
よって、3が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
段組み図形の外周の長さを求める問題でした。
解説の図のように、各段を長方形と扇形に分割して考えられるか?が第1のポイントです。
この見方ができれば、\(n\)段目の底辺を半径と\((n-1)\)段目の底辺の長さを用いて表せることに気がつくでしょう。
\(l_n\)を\(r\)と\(l_{n-1}\)で表したら、いかにして\(l_{60}\)を求めるか?が第2の関門です。
解説のように、\(l_n-l_{n-1}\)の形に変形して、区間\(2≦n≦60\)で和をとればOKです。
何気なく処理してますが、隣り合う項の差(階差数列といいます)で和をとるのは定石ともいえる解法です。
和をとると、中間の項(\(l_2〜l_{59}\))がプラスマイナスで打ち消し合って\(l_{60}\)と\(l_1\)だけが残るので、初期条件から\(l_{60}\)を求めることができます。
数列関連の問題で時折見かけるテクニックなので、ぜひ覚えておいてくださいね。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!次回もお楽しみに!
次回もお楽しみに!
略解
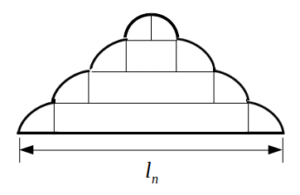
段組み図形の外周の長さを求める
図のような補助線を加えると、各段は長方形と半径\(r\)の四半分の扇形2つからなることが分かる。
\(n=60\)のとき、両側には120個の四半分の扇形があるので、
\(\frac{\pi}{2}r×120=60\pi r\)
また、最下層の底辺を\(l_n\)とおけば、
\(l_n=l_{n-1}+2r\)
すなわち、\(l_n-l_{n-1}=2r\)
両辺を、区間\(2≦n≦60\)で和をとると、\(l_{60}-l_1=118r\)
\(l_1=2r\)であるから、\(l_{60}=118r+l_1=120r\)
よって、\((外周の長さ)=60\pi r+l_{60}=60(\pi+2)r\)
したがって、3が正解である。

コメント