こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
そろそろ花粉が気になるこの季節、花粉症がそこまでひどくない身体をありがたく思ってます。
私は鼻詰まりがあるくらいですが、敏感な方は大変みたいですね。
帰宅したときは必ず玄関先で花粉を払っている、なんて話は聞いたことがあります。
小さい頃から花粉症に悩まされたことはなく、鼻詰まりもここ数年になって表れた症状なんですよね。
丈夫(鈍感?)な身体に感謝です。
前回は、サッカーの総当たり戦の問題をやりましたね。
各チーム各試合の得点状況を、条件にしたがって明らかにする問題でした。
まだ問題を見てない方は、ぜひ挑戦してみてください。
今回のテーマは「展開図」です。
展開図のコツは「面移動」をマスターすることです。
以下の記事では、展開図の面移動について導入から説明しているので、不安のある方は参考にしてください。

展開図の面移動は、カレーの福神漬くらい大切(←??)
演習問題:切頂八面体の展開図
図は切頂八面体(正八面体の全ての頂点を切り落とした立体)の展開図である。この立体において、互いに平行な面に書かれた数字の和が全て等しいとき、※の面に書かれた数字として正しいのは次のうちどれか。
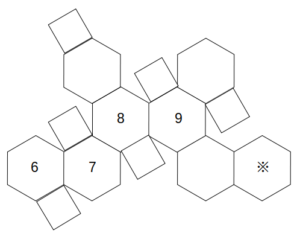
- 6
- 7
- 8
- 9
- 10
2
空間図形の、展開図を扱った問題です。
切頂八面体については問題文に説明があるので、実は基本的な正多面体の知識さえあれば解けてしまいます。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
展開図を切頂八面体から正八面体に直す
「切頂八面体」というのは聞き慣れない名前ですね。
問題文に、正八面体を元にした立体である、という主旨のヒントがあります。
切頂八面体のままでは扱いづらいので、展開図をもとの正八面体にもどしてみます。
切頂八面体の展開図から正八面体の展開図を復元すると、次図の赤線のようになります。
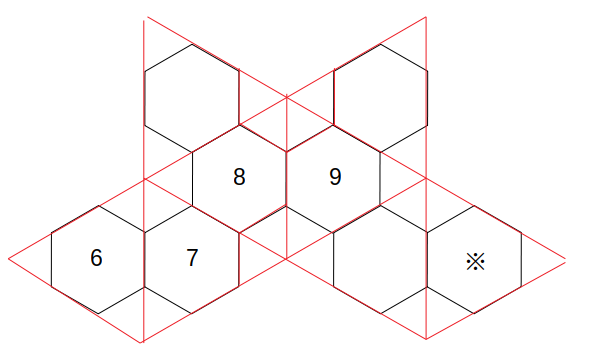

数字が書かれているのはいずれも正八面体の面だから、正八面体の展開図で考えればOK
面移動で展開図を見やすい形に変形
このままだと、もとの立体をイメージしづらいので、少し変形させます。
展開図では、組み立てて一致する辺同士はくっつけたり切り離したりできるのでしたね。
隣り合う辺は回転による面移動も有効
次図(左)の赤い太線同士をくっつけて、次図(右)のような展開図に書き換えます。
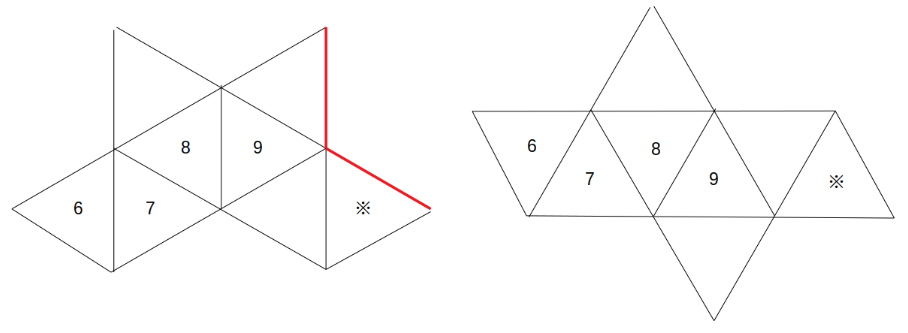
見慣れた正八面体の展開図になりました。
ここまで来れば、あとは正八面体の知識だけで解けます。
正八面体の展開図で、4つの面が一直線上にある場合、その両端にある面同士が向かい合います。
上の図の場合、6と9の面および8と※の面がそれぞれ向かい合うことになります。
6+9=8+※より、※=7
よって、2が正解です。
おわりに:展開図を解くためのポイントは「面移動」
お疲れ様でした!
いかがだったでしょうか?
展開図のコツは「面移動」です。
面移動は展開図の攻略に必須のテクニックなので、ぜひマスターしましょう。
過去の記事も参考にしてください。
展開図上で、互いに平行な面に書かれた数字の和が等しくなるような数字を選ぶ問題でした。
与えられた展開図は切頂八面体のものですが、六角形が正八面体の面にあたることに気づけば、もとの展開図のままでも正答を得ることはできます。
しかし、もとの展開図だと2つ目の図に示した面の移動がイメージしづらいので、解説では正八面体を復元して考えてます。
ただし、正八面体の展開図を得られても、向かい合う面に関する知識がないとここで止まってしまいます。
「正八面体の展開図で、4つの面が一直線上にある場合、その両端にある面同士が向かい合う」というのは覚えておいてください。
向かい合う面は展開図に多いテーマなので、どの面が向かい合うのか、法則をしっかりと暗記しておくことが大切です。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!次回もお楽しみに!
次回もお楽しみに!
略解
切頂八面体の展開図から正八面体の展開図を復元すると、次図(左)のようになる。
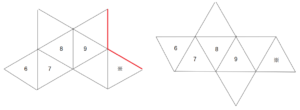
展開図の変形
この図(左)における赤い太線は、組み立てたときに重なる辺であるから、※の三角形を移動させて図(右)のような展開図を得る。
正八面体の展開図において、一直線に並んだ4つの面があるとき、両端の面は互いに平行となる。
6+9=8+※より、※=7
したがって、2が正解である。

コメント