【国家一般職】数的処理でよく出る速さの解き方３つまとめたよー【船の航行する速さと川上りにかかる時間】

こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます！
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。

今回のテーマは「速さ」です。
速さの公式は小学校で習うもので、定義自体はさほど難しくはありません。

しかし、定義だけで解けるほど単純な問題は、数的処理にはほぼありません。
数的処理で問われるのは、速さの公式を基礎にした応用力です。
状況を図示したり、比や方程式、グラフといった数学の知識も援用する必要があります。

この記事では、数的処理の「速さ」に関する問題を解くためのコツである「解法のポイント」を紹介します。
それから過去問の類題を一緒に解いて理解してもらうことで、本番で使える解法を身につけていってもらいます！

講義：速さを扱った問題の解き方

速さの問題には、いくつか解き方のパターンがあります。

以下、一つずつ解説します。

【１】方程式を立てる

未知数を文字でおいて、条件を数式化するやり方です。
文字にするのは速さ/距離/時間のいずれかです。
知りたい数値をそのまま文字でおく場合もあれば、他の数値を求めた後に速さの公式を使って間接的に求める場合もあります。

（問）
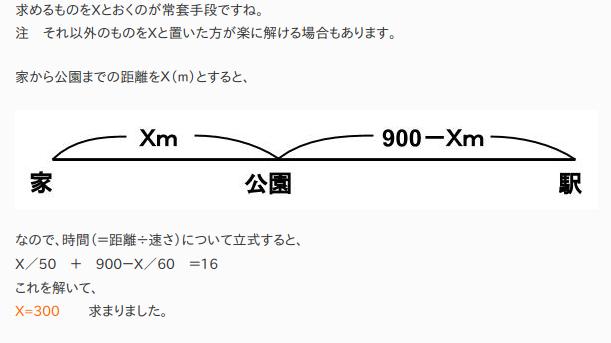
Aは朝８時に家を出発した。家から公園までは分速５０mで歩き、公園から駅までは分速６０mで歩いたところ、８時１６分に駅に着いた。家から駅までの道のりは９００mである。家から公園までの道のりは何mか。

（答）

（別解）

上の例題は、道のりを問うたものです。
距離をXとおいて解くやり方が一つ。
もう一つ、時間をXとして求めたあと、速さの公式を使って距離を算出しています。

【速さ 基礎】① | 公務員試験数的処理解法テクニック KOMARO

どちらも方程式を立てて解く方法ですが、ダイレクトに距離を求めてもいいし、時間というパラメータを経由して公式から距離を求めることもできます。

【２】比を使う

比を使って処理する方法もあります。
取っつきづらいですが、慣れれば簡単な計算で解答を出せます。
「\(速さ＝\frac{距離}{時間}\)」の公式より、速さの比は距離の比および時間の逆比に等しくなります。

\[
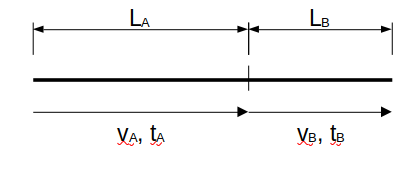
v_{A}:v_{B}=L_{A}:L_{B}=\frac{1}{t_{A}}:\frac{1}{t_{B}}
\]

（問）
長距離走大会にA、Bの２人が参加した。Aがスタートしてから３km地点にいたとき、Bは３００m後方にいた。その後Aがゴールしたとき、Bは７２０m後方にいて、Aがゴールしてから４分後にスタートした。このときAがゴールした時間として正しいのはどれか。ただし、A、Bの２人は同時にスタートし、２人は終始一定の速さで走ったものとする。
１．２０分
２．２４分
３．２８分
４．３２分
５．３６分

（答）
正解…５
Aが３０００m進んだとき、Bは３００m後方、つまり２７００m進んでいるので、AとBの速さの比は、
３０００：２７００＝１０：９です。
この２人が、スタートからゴールまで、同じ距離を進むのにかかる時間の比は９：１０、
その差が４分にあたるので、Aは３６分、Bは４０分でゴールしたことがわかります。

【速さ】問題３ | 公務員試験数的処理解法テクニック KOMARO

上の例題では、比を使って時間を求めています。
（距離の比）＝（速さの比）＝１０：９であり、これが「時間の逆比」に等しいので、
\(\frac{1}{t_{A}}:\frac{1}{t_{B}}\)＝10：9
つまり、\(t_{A}:t_{B}\)＝９：１０
ここでは\(t_{B}=t_{A}+4\)なので、
\(t_{A}=\)３６です。

【３】ダイアグラムを描く

時間（横軸）に対する位置（縦軸）をグラフ化したものが「ダイアグラム」です。
三角形を描き出して、相似の関係に持ち込んで図形的に解決する方法です。
グラフを描くには上に出てきた速さ/距離/時間の関係や比の関係に対する知識が必要で、ちょっと上級の解法です。

ある区間を行ったり来たりする問題には特に有効です。

（問）

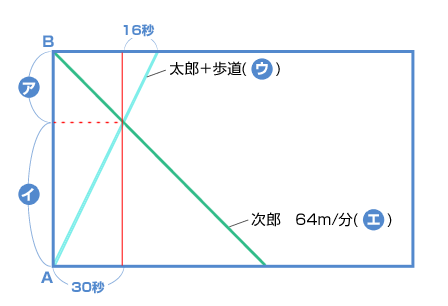
ある駅にはA地点からB地点へ向けて動く歩道があります。太郎君はA地点からB地点に向かってこの動く歩道上を毎分55mの速さで、次郎君はB地点からA地点に向かって普通（ふつう）の歩道を毎分64mの速さで同時に歩き始めました。2人は30秒後にすれ違（ちが）い、その16秒後に太郎君はB地点に着きました。動く歩道の速さは毎分 （1） mで、A地点からB地点までの距離（きょり）は （2） mです。
（芝中　2007年　2回）

（答）

右上と左下の直角三角形で、「16」と「30」が相似の比になっています。
だから、

で、次郎君と太郎君がそれぞれ進んだ距離（きょり）の比です。
つまり速さの比でもあるわけで、

64 × 15 ÷ 8 ＝ 120　　毎分120m （太郎君の歩く速さ ＋ 動く歩道の速さ）
よって、動く歩道の速さは、流水算の考え方で、

2人は30秒ですれ違（ちが）っているので、A地点からB地点までの距離は、

「速さとダイヤグラム」の解き方［中学受験］算数の頻出問題｜ベネッセ教育情報サイト

上の例題は、ダイアグラムで解く簡単な問題の例です。
図を描いて、直角三角形の相似から動く歩道とAB間の距離を求めています。
速さ一定なので直線で、あとは傾きと時間の大小関係を考慮してグラフ化します。

演習問題：船の航行する速さと川上りにかかる時間

一定の速さで流れる川を船で遡行する問題です。
基本に忠実に、「講義」の項の内容を思い出してください。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。

それでは、解説スタート！

問題文を見る

解説：速さを文字でおくと比の関係から方程式が立つ

求める数値は「時間」です。
距離が決まっているので、あとは速さが分かれば公式から時間を求められます。
「静水時における速さを１．５倍にして、〜」とあるので、これを\(1.5x\)とおきます。

選択肢が全て分単位で与えられているので、\(x\)の単位は「km/min（分速〜km）」とします。

こうすると、前半部において、上りと下りの速さはそれぞれ\(x-0.3\)、\(x+0.3\)と表せます。
（流速の単位変換：毎秒５m→毎分０．３km）

ここで上り下りの移動距離に注目。
速さの公式によると、速さと距離は比例の関係にあるんでしたね。
つまり、\(v_{A}:v_{B}=L_{A}:L_{B}\)

これを本問に適用すると、
\(x-0.3:x+0.3=4:10=2:5\)
よって、\(x=0.7\)[km/min]

さて、本問は「静水時における速さを１．５倍にして、A地点から１５km上流にあるB地点まで航行したとき」にかかる時間を求める問題です。
１．５倍の速さ→1.5×0.7＝1.05[km/min]

これは静水時の速さなので、上りだと1.05-0.3=0.75[km/min]
距離１５kmの移動の時間は、１５/0.75=20分

よって、３が正解です。

本問は方程式と比の合わせ技で解く問題でした。

おわりに：速さの解法は方程式と比とダイアグラム

お疲れ様でした！
いかがだったでしょうか？

速さの問題を解く方法は3つあります。
方程式を立てるか、比の関係を用いるか、ダイアグラムを描くか、です。
いずれか一つの解法で解ける場合もあれば、組み合わせて解くケースもあります。

今回は、流れが一定の川の遡上にかかる時間を問う問題でした。
いわゆる「流水算」というやつです。
「流水算はこれ」「旅人算ならこれ」と対処するより、同じ「速さの問題」として勉強した方が応用が利きます。
そのため、この記事では速さ一般の問題に対する解法を紹介しました。

最後までお読みいただきありがとうございました。

本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！

この記事が参考になったら、ぜひシェアしてください！

Tweet

次回もお楽しみに！

略解