こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、表記ミスがある食塩水の配合問題でした。
問題文がかなり長く、情報を取捨選択して読み取ることが求められる問題です。
ぜひ解いてみてください。
もう解いた方は、お疲れ様でした。
学んだことを定着させ、本番で活用するためにも、しっかり復習しましょう。
おすすめのやり方は「解法の一般化」です。
学んだ解法から、似た問題に使えそうな考え方を抽出し、インプットする勉強法です。
これは、過去問と全く同じ問題の出る可能性がほぼない数的の試験に対して有効です。
闇雲に解法を丸暗記するのではなく、重要なポイントに絞って頭に入れるようにしましょう。
本サイトにある「解法のポイント」を、ご自分で探してみましょう!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
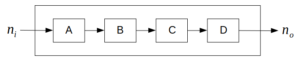
図のように、任意の入力値\(n_i\)に対し、4つの演算処理A〜Dを順に適用して得られる出力値\(n_o\)を返すシステムがある。A〜Dには、整数値\(n\)に対し、(I)「\(n+3\)」、(II)「\(3n\)」、(III)「\(n/2\)」、(IV)「\(n\)が偶数である場合は\(n-1\)、奇数である場合\(n-2\)」のうち互いに異なる1つがそれぞれ当てはまるものとする。いま、\(n_i\)としてある奇数の値を入力したところ、\(n_o=8\)であった。このとき、\(n_i\)としてあり得るのは次のうちどれか。
ただし、各処理の結果として得られる数値が整数でなかった場合は、以後の処理を中止してエラーが出力されるものとする。
- 3
- 5
- 7
- 9
- 11
2
システムの入力と出力に関する問題です。
A〜Dに当てはまる処理のパターンを考えましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
問題文の最後、「各処理の結果として得られる数値が整数でなかった場合は、以後の処理を中止してエラーが出力される」より、各処理の結果は全て整数となる必要があります。
本問では、(III)「\(n/2\)」の結果が整数となるような処理の順番を考えましょう。
(III)の結果が整数であるためには、(III)の前にある処理の数値が偶数でなければなりません。
\(n_i\)は奇数なので、次図の「?」、入力から(III)に至るまでのどこかの段階に、奇数→偶数の変化を含む処理が入ります。
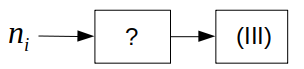
(I)〜(IV)のうち、奇→偶という変化が可能な処理は(I)「\(n+3\)」のみです。
したがって、「?」には(I)が入ります。
(I)と(III)の間には(II)と(IV)のいずれか(または両方)が入る可能性がありますが、(IV)「\(n\)が偶数である場合は\(n-1\)、奇数である場合\(n-2\)」だけはちょっと注意が必要です。
(IV)を行う前の\(n\)が偶数だった場合、\(n-1\)という処理によって奇数に変化するからです。
(I)と(III)の間に(IV)があると、せっかく(I)で得られた偶数の値が、(IV)によって再び奇数に変換されてしまい、その後の(III)でエラーとなってしまいます。
したがって、(IV)が(I)と(III)の間にあるパターンは除かなければなりません。
以上のことを踏まえて、あり得る処理手順のパターンを考えてみましょう。

図において、3つの丸印のいずれかに(II)または(IV)が一つずつ入ると考えると、並び方は
\[
{}_3 \mathrm{C}_2×2!=6通り
\]
丸印に(II)と(IV)が同居するパターンもあり得ます。
「(II)(IV)」というかたまりが、3つの丸印のいずれかに入ると考えて、並び方は
\[
{}_3 \mathrm{C}_1×2!=6通り
\]
以上より、処理手順は全部で6+6=12通り、
ではなく、ここから(IV)が(I)と(III)の間にあるパターンを差し引かなければなりません。
該当する並びは4通りあります。
よって、処理手順は全部で12-4=8通り
8通りなら、ギリギリしらみ潰しが可能ですね。
全て列挙してみます。
(IV)→(I)→(II)→(III)
(II)→(I)→(III)→(IV)
(IV)→(I)→(III)→(II)
(I)→(II)→(III)→(IV)
(II)→(IV)→(I)→(III)
(IV)→(II)→(I)→(III)
(I)→(III)→(II)→(IV)
(I)→(III)→(IV)→(II)
ここからは選択肢に挙がっている数値を入力値として、出力を計算します。
ゴリ押しで5×8=40回計算して終了、でもOKですが、ちょっと面白味に欠けるので、ここではもう少しスマートな解き方を紹介します。
40回もの計算をミスなく処理する、というのもなかなか難しい話だと思うので。
紹介するのは、8通りのうちから出力値が最大および最小となるプロセスを選び出し、\(n_o=8\)をその範囲に含む選択肢を候補として残す、という方法です。
……実際に見た方が早いでしょう。
まず、出力値が最大となるプロセスについて。
出力値を最大化するなら、(II)の直前の値が大きい方が有利です。
よって、(I)→(II)という順番が含まれると考えられます。
かつ、(IV)は引き算なので(II)よりも後にある方がよく、(I)→(II)→(IV)という順番になります。
これらの条件にマッチするプロセスは、「(I)→(II)→(III)→(IV)」と「(I)→(III)→(II)→(IV)」ですね。
(乗除の計算には交換法則があるので、(II)→(III)と(III)→(II)は同じ結果になります)
次に、出力値が最小となるプロセスについて。
この場合はさっきと反対で、(II)の直前の値をできるだけ小さい方が有利です。
よって、(入力値)→(IV)→(II)という順番だと考えられます。
これに当てはまるのは「(IV)→(II)→(I)→(III)」だけです。
これらをもとに、正解の選択肢を絞り込みます。
まず、1の「3」について、最大値を与えるプロセスに入力すると、\(n_o=7\)
最大値が7、ということは、8パターンあるプロセスのいずれを用いても8にはなり得ないので、候補から除外できます。
次に、2の「5」について、出力の最大値は11、最小値は6なので、8パターンのプロセスの中に\(n_o=8\)となるものがあり得ます。
3の「7」については、最小値は9なので候補から外れます。
同様に計算してみると、4の「9」と5の「11」も候補から外れることが確認できます。
結局、正解の候補は2の「5」しかありません。
実際、プロセス「(II)→(IV)→(I)→(III)」のとき、\(n_o=8\)となります。
よって、2が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
システムの出力値をもとに入力値を特定する問題でした。
パターン化しづらい問題なので、何から手を付けていいかよく分からなかったかもしれません。
問題文に散りばめられた条件をもとに、処理手順としてあり得るものを絞り込むのが第一歩。
そこに選択肢の数値を順に入力してしらみ潰しするわけですが、処理手順が8通りと少し多いので、一手間加えたスマートなやり方を解説では紹介しました。
ただ、これはあくまで理想論なので、実戦的には泥臭く8通り全てに5択を入力するやり方も大いにアリです。
いずれにしても、計算ミスには気をつけましょう。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
「各処理の結果として得られる数値が整数でなかった場合は、以後の処理を中止してエラーが出力される」より、各処理の結果は全て整数となる必要がある。
\(n_i\)は奇数なので、次図の「?」、すなわち入力から(III)に至るまでのどこかの段階に、奇数→偶数の変化を含む処理が入る。
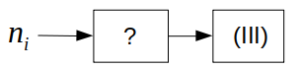
(III)の前の処理
(I)〜(IV)のうち、奇→偶という変化が可能な処理は(I)「\(n+3\)」のみなので、「?」には(I)が入る。
(IV)「\(n\)が偶数である場合は\(n-1\)、奇数である場合\(n-2\)」について、(IV)を行う前の\(n\)が偶数だった場合、\(n-1\)という処理によって奇数に変化してしまうので、(IV)が(I)と(III)の間にあるケースは候補から外す必要がある。

条件を満たす処理パターンを考える
図の○の位置に、(II)と(IV)のいずれか(または両方)が入るパターンのうち、上述の条件を満たすものだけをピックアップすると、以下の8通りが処理手順の候補として残る。
(IV)→(I)→(II)→(III)
(II)→(I)→(III)→(IV)
(IV)→(I)→(III)→(II)
(I)→(II)→(III)→(IV)
(II)→(IV)→(I)→(III)
(IV)→(II)→(I)→(III)
(I)→(III)→(II)→(IV)
(I)→(III)→(IV)→(II)
8通りの処理手順のうち、出力が最大/最小となるものを特定する。
まず、出力値が最大となるプロセスについて、出力値を最大化するなら、(II)の直前の値が大きい方が有利である。
よって、そこには(I)→(II)という順番が含まれると考えられる。
かつ、(IV)は引き算なので(II)よりも後にある方がよく、(I)→(II)→(IV)という順番ができる。
これらの条件にマッチするプロセスは、「(I)→(II)→(III)→(IV)」と「(I)→(III)→(II)→(IV)」
(乗除の計算には交換法則があるので、(II)→(III)と(III)→(II)は同じ結果になる)
次に、出力値が最小となるプロセスについて、この場合は(II)の直前の値をできるだけ小さい方が有利である。
よって、(入力値)→(IV)→(II)という順番が考えられる。
これより、最小の出力値を得る処理手順は「(IV)→(II)→(I)→(III)」と決まる。
1の「3」について、最大値を与えるプロセスに入力すると、\(n_o=7\)なので出力が8となることはなく、不適。
一方、2の「5」について、出力の最大値は11、最小値は6なので、8パターンのプロセスの中に\(n_o=8\)となるものがあり得る。
実際、8通りの処理手順において、それぞれ入力を「5」とすると、「(II)→(IV)→(I)→(III)」において\(n_o=8\)となる。
したがって、2が正解である。

コメント