こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「整数」
実は、かなり対策しやすい単元。
整数問題には型があり、解き方のパターンが決まっているから、パターンごとに狙いを絞った対策が可能なんです。
整数問題の「型」とは、【範囲、書き出し、しらみ潰し】
苦手な人も、まずはこの解き方の流れを練習してみてください。

知っているだけでもかなり有利になる
本サイトでは、整数問題でよく使われる解き方の流れを「解法のポイント」としてまとめています。
- 範囲を絞る
- 倍数、約数、余りから候補を書き出す
- しらみつぶしで特定
「解法のポイント」を念頭におきながら、今回も数的処理の過去問みたいな問題を解いていきます。
演習問題:株取引の利益と整数
X氏は、A〜Dの4社と株取引をすることにした。株は1口から購入でき、口数に比例して年ごとに一定の利益が得られるものとする。X氏は、一年ごとに必ず持っている株を全て売却するという条件のもと、会社ごとに予算を決め、3年の間に購入する株の合計額が予算を超えることのないようにした。次表は、4社の年ごとの利益とX氏が決めた予算の一覧である。年ごとの取引について、次のことが分かっているとき、確実にいえるのはどれか。
ただし、利益は変動せず常に一定であったものとする。
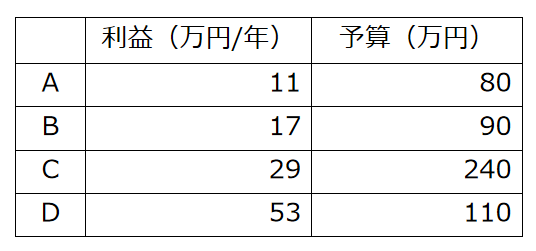
- 1年目は、D以外の3社の株をそれぞれ1口以上購入した結果、計120万円の利益を得た。
- 2年目は、AとC、およびBとDの口数が同じとなるように、4社全ての株をそれぞれ1口以上購入した結果、計230万円の利益を得た。
- 3年目は、4社全ての株をそれぞれ1口以上購入した結果、計150万円の利益を得た。
- 2年目にBの株を2口購入した。
- 2年目にCの株を1口購入した。
- 3年目にAの株を2口購入した。
- 3年目にDの株を2口購入した。
- 3年目に購入した株の口数の合計は奇数であった。
3
たまにある、お堅いテーマ。
小難しい文章にだまされないで。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:整数の範囲を決めて総当たり
選択肢を見ると、何をすべきか分かります。
選択肢はいずれも何年目にどの会社の株をいくつ買ったのか、という内容。
そして、条件は年ごとの利益の合計額。
1口あたりの額は与えられているので、口数を文字でおけば合計額の関係を方程式で表せます。
方程式を解けば、口数が分かります。

そうだ、条件を方程式にしてみよう
1年目:整数は「いくつまで?」が重要

1年目に買った口数を(A, B, C)=(\(a_1+1,b_1+1,c_1+1\))とおけば、合計額について
\[
11(a_1+1)+17(b_1+1)+29(c_1+1)=120 \\
→11a_1+17b_1+29c_1=63……(\mathrm{i})
\]
ここで(\(a_1,b_1,c_1\))は整数(=口数)、という隠れた条件を使うと、あら不思議。
たった一つの方程式から、(\(a_1,b_1,c_1\))を全て特定できるんです。

\(a_1\)は0スタートね
整数問題には解き方のパターンがある、と言いました。
「解法のポイント」を思い出します。
- 範囲を絞る
- 倍数、約数、余りから候補を書き出す
- しらみつぶしで特定
範囲をしぼる
まずは(\(a_1,b_1,c_1\))の【範囲を絞り込み】ます。
株の口数は無限に増やせるんでしょうか?
そんなことはないはず。
物事には必ず終わりがあるものです。

スマホゲーのガチャですら天井があるしね
本問では、予算が天井です。
口数の制限を書いておきます。
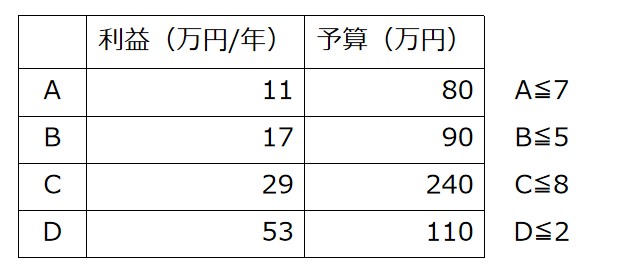
この制約のもと、例えば\(c_1\)の上限を考えてみます。
\(c_1=0,1,……\)と増やしていくとき……
右辺(=63)を満たすには\(c_1\)が2以下である必要があると分かります。

\(c_1=3\)以上だと63を超えてしまう

つまり、0≦\(c_1\)≦2
書き出し&しらみつぶし
範囲が決まったら、【書き出してしらみつぶし】です。
\(c_1\)は0以上2以下の整数。
→\(c_1\)=0 or 1 or 2
\(c_1\)=0, 1, 2を、全て(i)へ代入します。
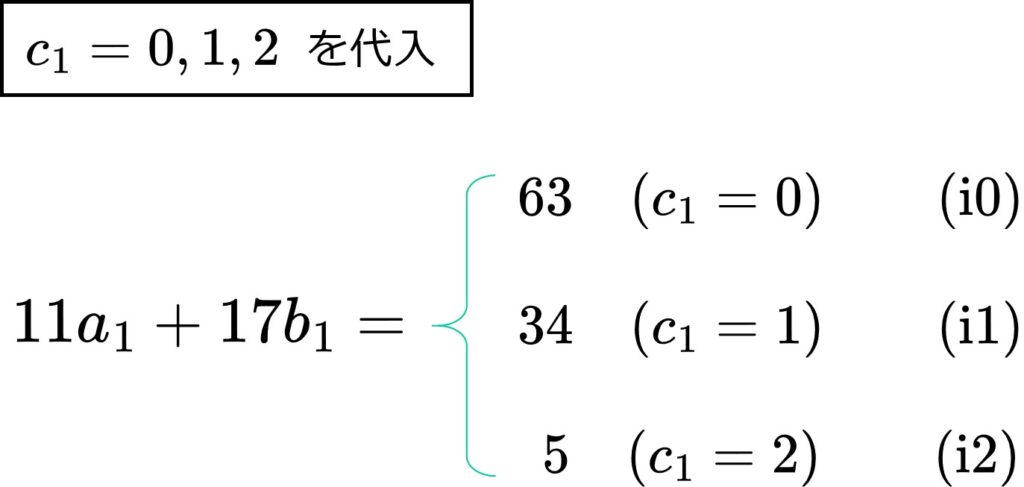
それぞれ、「A=~」の形に変形しますと、
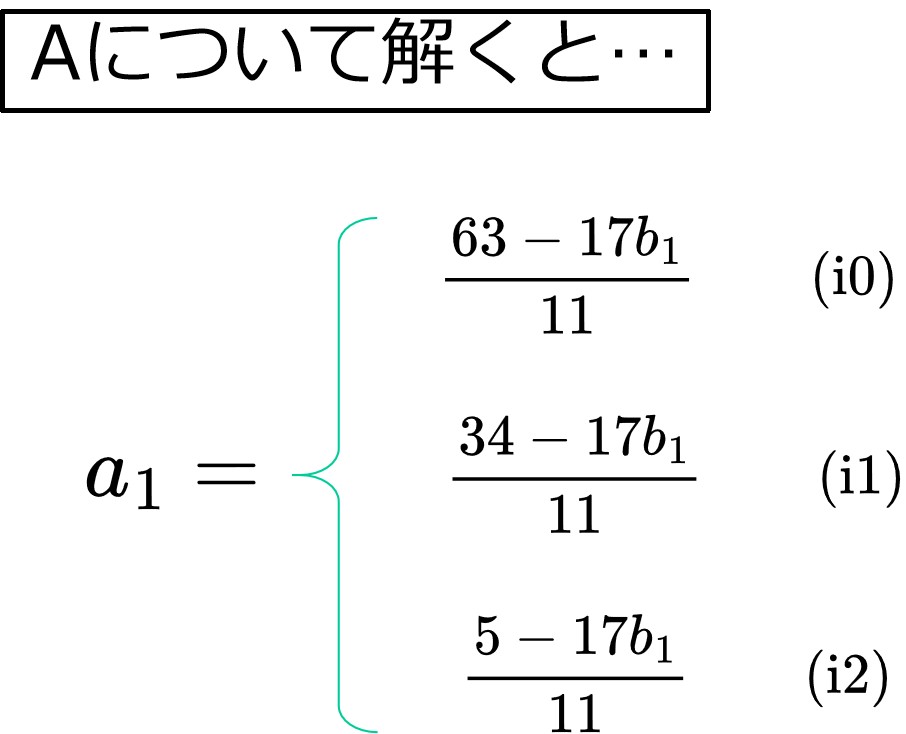
(i0)~(i2)のそれぞれで、\(b_1\)についてしらみつぶしします。
「\(a_1\)=整数」となる整数\(b_1\)を見つければOK。
(i0)~(i2)に対し、\(b_1=0,1,\)……を代入していくと、Aが整数となるのは、、、
(i1)で、\(b_1=2\)のとき\(a_1=0\)
↑これだけ。
よって、(\(a_1,b_1,c_1\))=(0,2,1)

+1に注意
2&3年目についても、同じように口数を求められます。
2年目:未知数(整数)は実質的に2つ

口数を(A, B, C, D)=(\(a_2+1,b_2+1,a_2+1,b_2+1\))とおけます。
合計額の方程式は、
\[
11(a_2+1)+17(b_2+1)+29(a_2+1)+53(b_2+1)=230 \\
→4a_2+7b_2=12 \\
→a_2=3-\frac{7b_2}{4}……(\mathrm{ii})
\]
\(a_2\)は整数、ということは、\(\frac{7b_2}{4}\)も整数のはず。
→\(b_2\)=0あるいは4の倍数

\(b_2\)=0 or 4 or 8 or ……
ここでもやはり【範囲を絞る】ことが必要になります。
式(ii)によると、\(b_2\)は4以上にはなれないことが分かります。(\(a_2\)は0以上)
つまり、\(b_2=0\)とするしかなく、\(a_2=3\)

+1を忘れずに
3年目:候補の数が少ない整数で総当たり

合計額について、
\[
11(a_3+1)+17(b_3+1)+29(a_3+1)+53(b_3+1)=150 \\
→11a_3+17b_3+29c_3+53d_3=40……(\mathrm{iii})
\]
再び、式(3)を眺めます。
左右が等しくあるためには、\(d_3=0\)とするしかありません。
→\(11a_3+17b_3+29c_3=40\)
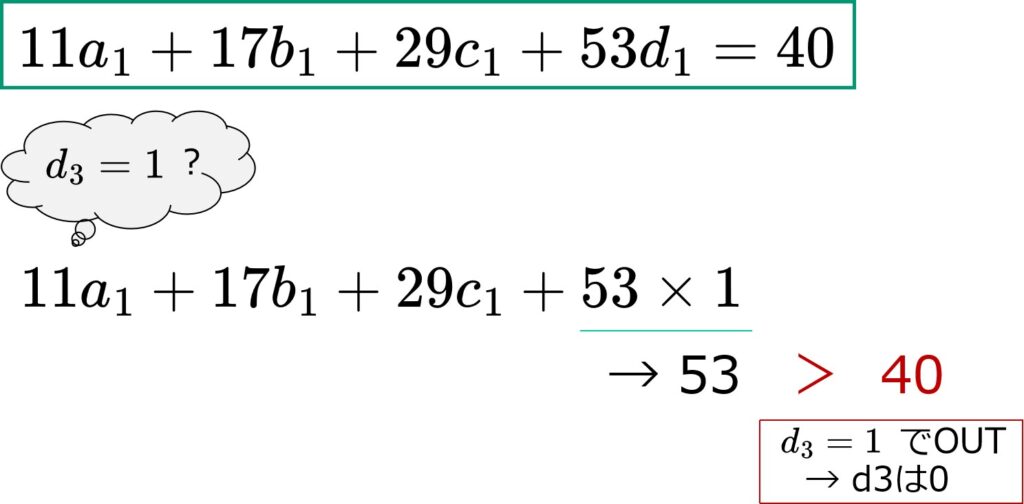
Bについて。
Bの上限は5ですが、2年目までで4口買っています。
かつ、「4社全ての株を1口以上」
ということで、\(b_3=0\)に決まります。
→\(11a_3+29c_3=40\)
同じように式変形しますと、
\[
a_3=\frac{40-29c_3}{11}
\]
\(c_3=1\)であれば、分子が11の倍数となって約分できます。
このとき、\(a_3=1\)
| 1年目 | 2年目 | 3年目 | 計 | 予算(万円) | |
| A | 1 | 4 | 2 | 7(77万円) | 80 |
| B | 3 | 1 | 1 | 5(85万円) | 90 |
| C | 2 | 4 | 2 | 8(232万円) | 240 |
| D | 0 | 1 | 1 | 2(106万円) | 110 |
表をもとに選択肢を検討しますと、正しいのは3。
よって、3が正解です。
おわりに:範囲の整数を書き出してしらみつぶし
お疲れ様でした!
整数問題を解く3ステップは、【範囲、書き出し、しらみ潰し】
未知数が整数である限り、範囲が決まれば候補を書き出せます。
候補が挙げられればしめたもの。
あとは候補を一つ一つ式に当てはめて、矛盾のないものを探せばいいわけです。
「解法のポイント」について、詳しく知りたい方は以下の記事へ。
余りの問題の記事はこちら↓
ちょっと難しめの、総合職のやつも載せときます。
「モクセイ」で検索したらゲームのキャラがヒットした

中盤に出てくるボスキャラだった。ちなブサイク
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!





コメント