こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
白米と玄米を同じように水に浸して数日放置すると、白米は黒く変色してしまうのに、玄米は芽が出てツルが伸びてくるんだそうです。
玄米にはまだ生物としての機能が残っているのが分かりますよね。
「白米よりも玄米の方が健康的」とはよく言われますが、こういう実験を知って、私も食生活に玄米を取り入れてみたくなりました。
前回は、条件に合う3つの自然数を特定する問題をやりましたね。
国家総合職で頻出の整数をテーマにした問題で、整数の性質の扱い方を学べるので、解いてない方はぜひ挑戦してみてください。
もう解いた方は、忘れないうちに復習するようにしてください。
「忘れないうちに」というのがポイントで、忘れてから復習するとなると、また一から解説を読み込む羽目になりますが、それは面倒ですよね。
であれば、まだかすかに記憶が残っているうちに要点だけでも思い出して、脳内で完結させる方が遥かにオトクだと思うんです。
さっと復習する、を何度も繰り返すのがコツです。
復習がバッチリな方は、本日の問題へ参りましょう。
本日の演習問題
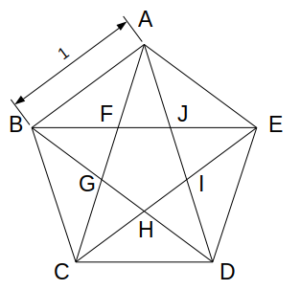
図のような1辺の長さが1の正五角形ABCDEにおいて、対角線の交点をF、G、H、I、Jとすると、五角形FGHIJもまた正五角形となる。このとき、正五角形FGHIJの面積は正五角形ABCDEの面積の何倍か。
- \(\frac{1}{9}\)倍
- \(\frac{3}{25}\)倍
- \(\frac{7-3\sqrt{5}}{2}\)倍
- \(5-2\sqrt{2}\)倍
- \(\frac{23-8\sqrt{7}}{9}\)倍
3
正五角形の面積比に関する問題です。
通常、面積は公式などにより直接求めるか、あるいは相似比を経由するのが一般的です。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
面積を求める方法については、前に正方形を折り返す問題でも述べましたが、基本的には以下の2つのうちのいずれかを用いることになります。
- 大きさが分かっている図形との比から求める方法
- 具体的に長さを求めて面積公式に当てはめる方法
本問では「正五角形ABCDEの面積の何倍か?」を聞かれていることより、1の方法を使います。
もう一歩踏み込むと、正五角形どうしの面積比なので、相似比が分かれば求められますね。
もっと言うと、基準となるABCDEの1辺の長さが与えられているので、あとはFGHIJの1辺の長さが分かればOKです。
以下、正五角形FGHIJの1辺の長さを求める方針でいきます。
まず、AB=BC=AE=1
また、正五角形の内角は等しいので、∠BAE=∠ABC=∠AED=108°
よって、△ABE≡△BCA≡△EAD
これより、∠BAF=∠FBA=36°なので、△FABはFA=FBの二等辺三角形と分かります。
△ABE、△BCA、△EADは全て底角が36°の二等辺三角形なので、∠FAJ=108°-36°×2=36°
よって、∠ABJ=∠FAJ=36°
これと∠AJF=∠BJA(共通)より、△AFJ∽△BAJ
さらに、∠BJA=∠BAF+∠ABF=36°+36°=72°
また、∠AJF=∠JEA+∠JAE=36°+36°=72°=∠BJA
よって、△AFJ(および△ABJ)はAF=AJ(BA=BJ=1)の二等辺三角形です。
以上より、FJを\(x\)とおくと、次図のように各辺の長さが決まります。
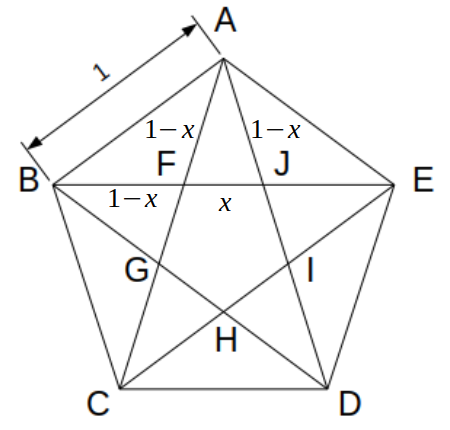
△AFJ∽△BAJより、AB:AF=AJ:FJ
すなわち、\(1:(1-x)=(1-x):x\)
これを解くと、\(x=\frac{3-\sqrt{5}}{2}\) (前提条件0<\(x\)<1に注意)
よって、正五角形ABCDEとFGHIJの相似比は\(1:\frac{3-\sqrt{5}}{2}\)
これより、面積比は\(1^2:(\frac{3-\sqrt{5}}{2})^2=1:\frac{7-3\sqrt{5}}{2}\)
したがって、3が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
正五角形に対角線を引いてできる正五角形の面積を求める問題でした。
今回はFGHIJが正五角形であることは問題文に書いてあったので、1辺の長さが分かれば相似比と面積比の関係からFGHIJの面積を知ることができました。
問題で与えられなかったとしても、FGHIJが正五角形となることは図形の対称性を考えればすぐに分かります。
きちんと証明しようとすれば手間がかかりますが、教養試験は短答式なので、それくらい大ざっぱな理解で大丈夫です。
むしろ、数的処理の図形問題で完璧主義は足かせとなりやすいです。
特に理系の方であれば、「きちんと証明しなければ」と思ってしまう気持ちは分かりますが、数的処理ではいち早く正解にたどり着くことが最優先事項です。
きちんと証明できなくても、図を描いて「それっぽいな」と思ったことは使ってしまった方がいいと思います。
そうして選択肢のいずれかにたどり着いたら、それをマークして次の問題に移るのが賢明です。
数的処理は圧倒的に時間が足りない試験なので、解答までの手数を少しでも減らすように工夫することが必要になります。
100%自信のある解答1つより、70〜80%くらいの出来の解答3つの方が高得点には結びつきやすいです。
完璧主義な方はぜひ肩の力を抜いて、自分なりの抜け道を発見する練習もしてみてください。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
また、正五角形の内角は等しいので、∠BAE=∠ABC=∠AED=108°
これとAB=BC=AE=1より、△ABE≡△BCA≡△EAD
これより、∠BAF=∠FBA=36°であるから、△FABはFA=FBの二等辺三角形である。
△ABE、△BCA、△EADは全て底角が36°の二等辺三角形であるから、∠FAJ=108°-36°×2=36°
よって、∠ABJ=∠FAJ=36°
これと∠AJF=∠BJA(共通)より、△AFJ∽△BAJ
さらに、∠BJA=∠BAF+∠ABF=36°+36°=72°
また、∠AJF=∠JEA+∠JAE=36°+36°=72°=∠BJA
よって、△AFJ(および△ABJ)はAF=AJ(BA=BJ=1)の二等辺三角形である。
以上より、FJを\(x\)とおくと、次図のように各辺の長さが決まる。
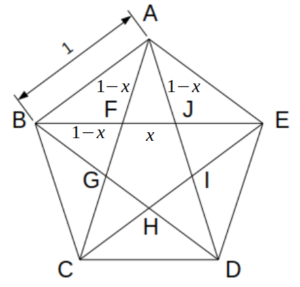
FJ=xとおく
△AFJ∽△BAJより、AB:AF=AJ:FJ
すなわち、\(1:(1-x)=(1-x):x\)
これを解くと、\(x=\frac{3-\sqrt{5}}{2}\) (前提条件0<\(x\)<1に注意)
よって、正五角形ABCDEとFGHIJの相似比は\(1:\frac{3-\sqrt{5}}{2}\)
これより、面積比は\(1^2:(\frac{3-\sqrt{5}}{2})^2=1:\frac{7-3\sqrt{5}}{2}\)
したがって、正解は3である。

コメント