こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「転がる円の回転数」
数的処理の平面図形で、円の回転数を問う問題が出ることがあります。
図形の周りを滑らずに転がる円の回転数を求めよ、というやつ。
一度は見たことがあるはず。
しかし、これに的を絞って対策する、ということもなかなかないかもしれません。
かなり限定的なテーマですし、つい後回しにしてしまうと思います。

やれるときにやろうと思ってやらないパターンはありがち
そんな方も、一度本腰を入れて対策しておくことをオススメします。
というのも、この手の問題は解き方を知っていれば対処できるものも結構多いんです。

周りがやらないから一歩リードできる
この記事では、滑らずに転がる円の回転数を求める公式を2通り紹介。
後半では、過去問に似せた演習問題を解きながら、コツの使い方を学びます。
講義:転がる円の回転数の公式は2つ
転がる円の回転数を求めるには、大きく2通りの方法があります。
- 小円の中心の移動距離÷小円の円周
- \(\frac{大円の円周}{小円の円周}\)+1
順に解説します。
【1】転がる中心の移動距離÷転がる円周
回転数の問題でよく知られた解き方です。(筆者調べ)
まずはこちらの解き方を覚えましょう。

(筆者調べ)←これのアテにならなさハンパないよ
まず、中心が描く軌道の形を捉えるのが第一歩。
円と円、円と正方形など、ありがちな図形は覚えてしまうのが吉。
中心の経路長を求めたら、小円(転がる円)の円周の長さで割れば回転数が分かります。
特に中心の軌道が円であれば、半径の比(円軌道÷小円)でも求められます。

「センターラインの公式」とか「中心線の公式」っていうらしいよ
なぜこれで回転数が分かるのか?
こちらのサイトで、半径を変えて何通りか調べてみると、正しいっぽいことが確認できます。
実験してみてください。
厳密ではありませんが、これでも納得はできますね。

ときに深追いは禁物
もう少し説明が欲しい、という方へ。
上のサイトにもあるように、転がる道のりを延ばして直線にしてみます。
この場合の「滑らずに1周する」とは、直線を端から端まで転がる、ということです。
すると、図のように、中心が描く軌道も直線で、長さは転がる道のりと等しくなることが分かります。
円周に沿って回転する円の回転数|みんなの算数オンライン
例題1:円が円の外周を転がるケース
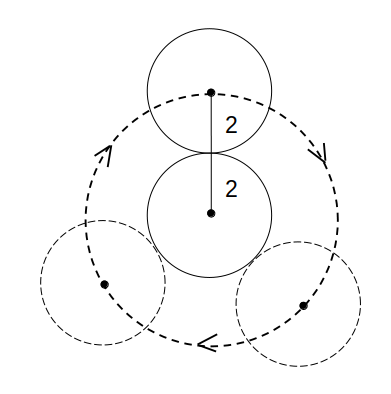
半径2の円を2つ用意し、一方が他方の外周を滑らずに1周するとします。
小円の中心は、半径4の円を描きます。
→\(\frac{2\pi × 4}{2\pi × 2}=2\)(回転)
例題2:円が正方形の外周を転がるケース
1辺の長さが4の正方形の外周を、半径2の円が滑らずに1周するとします。
中心の軌道を正しく捉えられるかがカギ。
実際に描いてみたものが次の図です。

(生地をオーブンに入れて)3分経ったものがコチラ。
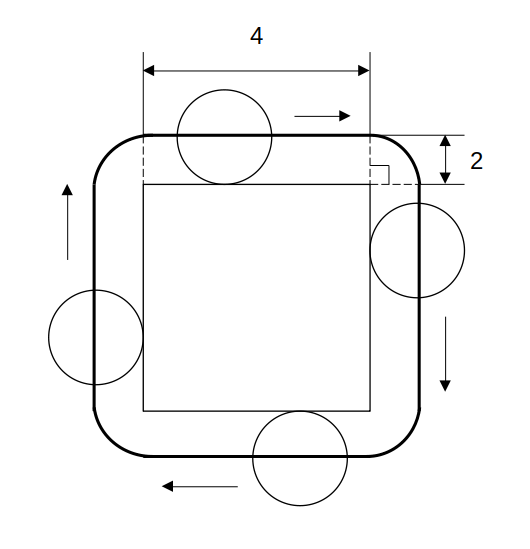
経路の長さは、直線部分と四隅に分けて考えればOK。
直線:長さ4が4本→4×4=16
四隅:半径2のおうぎ形(90°)が4つ→4π
これより、回転数は
\(\frac{16+4\pi}{4\pi}=\frac{4}{\pi}+1\)(回転)
【2】\(\frac{大円の円周}{小円の円周}\)+1
円周の長さの比に、1を加えるやり方。
中心の移動距離が転がる距離に等しい場合は、この公式が使えます。

上で出た、円が円の上を転がるケースはOK
やはり道のりを直線になおして考えます。
円周に沿って回転する円の回転数|みんなの算数オンライン
滑らずに転がる、ということは、小円の中心が円周の長さだけ移動したときが小円の1周に相当します。
であれば、(大円周)÷(小円周)で回転数が求められそうですね。
ところが、これだけでは不正解。
上の考察は、あくまで転がる道のり(=大円)を直線になおした場合の考え方。
実際は円形なので、補正を加えることが必要となります。
公式の「+1」は、小円の中心が1周したことによるもので、直線→円の変換に必要な素材です。

山奥に棲むドラゴンの牙みたいなモンです
地球の天体運動をイメージしてください。
自転(割り算)は昼夜の入れ替わり、公転(+1)は季節の移ろい。
転がりによる回転(割り算)と中心の回転(+1)は、別々に考えて足し合わせます。
次の説明も参考になります。
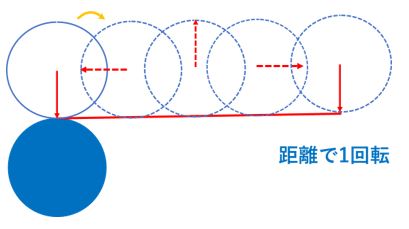
距離で1回転=自転、形で1回転=公転です。
また、次のような別の考え方でも確認してみることができます。
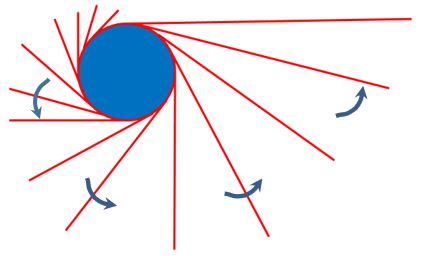
真ん中の青い円の周りには赤いひもが巻いてあります。
この赤いひもを切ってほどいてみます。
するとこんな下図のような状態になります。巻いてあった赤いひもの長さは回転する円の周りの長さと等しいので、
この赤いひもの上を滑らずに右方向に動くとちょうど1回転します。実際に1周分の距離を回転しているので
この1回転を距離で1回転すると呼ぶことにしましょう。次にこの赤いひもを真ん中の青い円の周りに再び巻き付けて
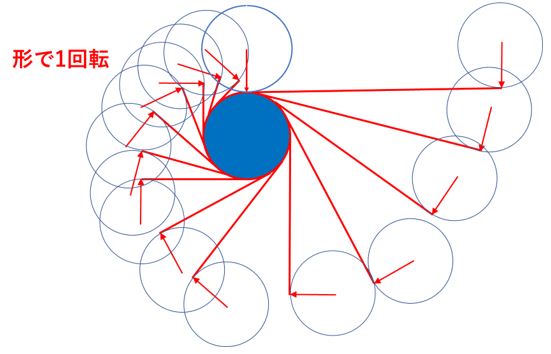
最初の状態に戻してみます。ご覧のようにひもを巻き付けるだけで外側の円が1回転していることが矢印を見ると
確認することができますね。
この1回転を形で1回転すると呼ぶことにしましょう。このように真ん中の円の周りを外側の円が滑らずに1周動いたとき
円周の周りを円が動くと何回転するの?|中学受験プロ講師ブログ
距離で1回転、形で1回転したということがいえます。
例題1:円周の比で解く
半径2の円が、半径2の円の周上を1周するから、
\(\frac{2\pi × 4}{2\pi × 2}=2\)(回転)

ね、簡単でしょ?
例題2:円が正方形の外周を転がるケース→×
1辺の長さが4の正方形の外周を、半径2の円が滑らずに1周するとします。
この例では、【2】の公式は使えません。
【2】は、中心の移動距離が転がる距離に等しいことが前提だからです。
この例であれば、四隅を転がるときを考えてみてください。

角を曲がる間、円はずっと頂点で接します。
この間、中心は移動しているのに、転がる距離は増えません。
つまり、(中心の移動距離)≠(転がる距離)であり、【2】は使えません。
以上、滑らずに転がる円の回転数を求める公式の解説でした。
ここからは、過去問をもとに作ったオリジナルの演習問題を解きながら、「解法のポイント」の使い方を学んでいきます。
演習問題:転がる内接円/外接円の回転数の比
3つの円αβγが、図のように配置された、3つの円αβγがある。αは点Pでβに内接し、γは点Qでβに外接する。αの半径は3、βとγの中心間の距離は13、βとγの共通接線RSの長さは12である。いま、固定したβの内周および外周を、それぞれαおよびγが滑ることなく1回転して元の位置に戻るとき、αとγの回転数の整数比はいくらか。
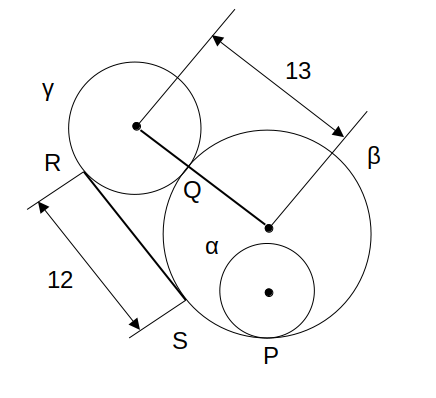
- 5:12
- 6:13
- 7:11
- 8:13
- 8:15
4
内接円/外接円の回転数の問題。
回転数を知るには、何が必要でしょう?
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:3円の半径から回転数へ
回転数とは、ざっくり言うと「大円の円周は小円の何倍か?」ということ。
言い換えると、半径の比によって決まります。

(半径の)2π倍は約分で消える
与えられた図を見ると、半径は図形的に求められそう。
そこで、以下は半径を求めていきます。
共通接線&補助線で半径を求める
αβγの中心を、それぞれA、B、Cとします。
図形問題といえば、補助線。
BとS、CとRをそれぞれ結びます。
さらに、CからBSへ向かって垂線CHを下ろします。
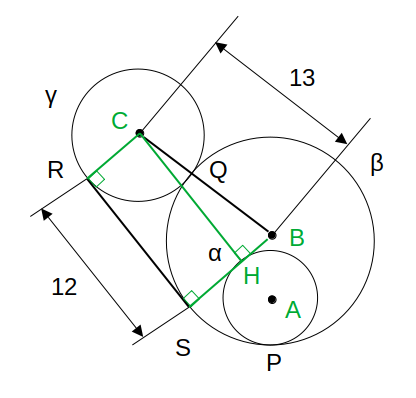
接線の性質より、BS⊥RS、CR⊥RS
これとBS⊥CHより、CH//RS
よって、CHSRは長方形で、CH=RS=12
△BCHは直角三角形なので、三平方の定理が使えます。
\(12^2+\mathrm{BH}^2=13^2\)より、BH=5
さて、目標は半径を求めることでした。
β、γの半径をそれぞれ\(b,c\)とおきます。
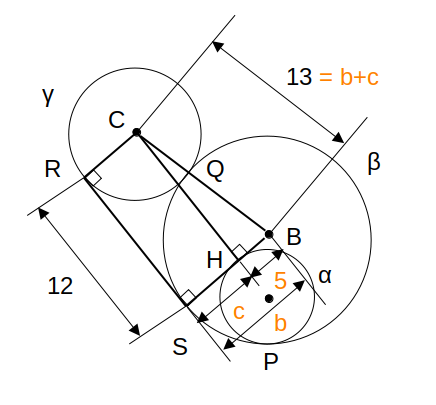
中心間の距離について、\(b+c=13\)…(i)
BHについて、\(b-c=5\)…(ii)

BH=BS-HS、HS=CR=\(c\)ってことね
(i)と(ii)を連立方程式として解くと、
(\(b,c\))=(9, 4)
中心の経路÷転がる円の円周で回転数
αβγの半径が出そろいました。
ここからは、内接円/外接円の回転数の問題。
記事の前半で紹介した「解法のポイント」が、ようやく登場します。
- 小円の中心の移動距離÷小円の円周
- \(\frac{大円の円周}{小円の円周}\)+1
αについて、中心Aは半径6の円を描きます。
軌道の長さは、\(2\pi × 6\)
これに対し、αの円周は\(2\pi × 3\)
よって、回転数は\(\frac{2\pi × 6}{2\pi × 3}\)=2
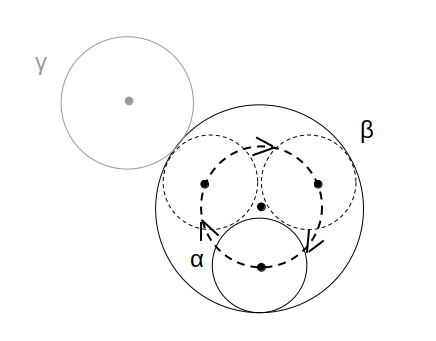
γについて、中心Cは半径13の円を描きます。
軌道の長さは、\(2\pi × 13\)
これに対し、γの円周は\(2\pi × 4\)
よって、回転数は\(\frac{2\pi × 13}{2\pi × 4}\)=\(\frac{13}{4}\)
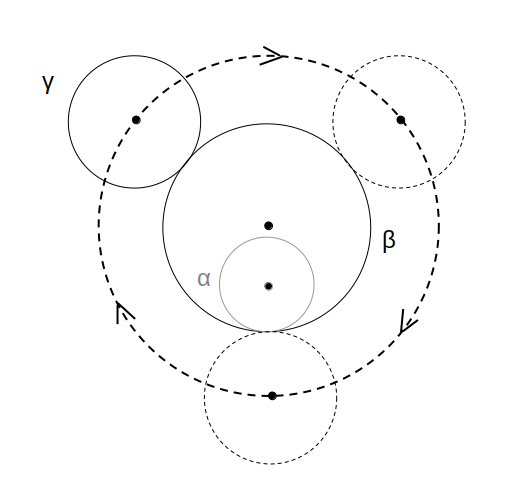
これより、回転数の比は\(2:\frac{13}{4}=8:13\)
よって、4が正解です。
おわりに:円の回転数は「中心の経路」か「円周の比」で
お疲れ様でした!
滑らずに転がる円の回転数を求める方法は2つ。
【1】中心の経路長から求める
【2】周長に注目する
まずは【1】を覚えましょう。
典型問題なら、この解き方で対応できます。
理屈で覚えるのが得意なら、【2】もオススメ。
天体の自転と公転に置き換えるとイメージしやすいです。
今回は、円の内外を転がる2円の回転数の比を求める問題でした。
回転数の比が半径の比に相当することに気づいたら、まずは図形的に半径を求めます。
垂線を引いて、台形を「長方形+直角三角形」に分解するのがポイント。
共通接線の問題は、以下の記事も参考になります。
半径が求められたら、あとは転がる円の問題。
解説は【1】で解いてますが、【2】でもOK。
【2】なら、中心の軌道を考えずとも半径だけで比を出せます。
☆正四面体コロコロ
アゴ痛くて口開かないのにサムライマックのトリプル食った

箸で細かくしながら食べた。うまかった。
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
αβγの中心を、それぞれA、B、Cとする。
次図のように、補助線BSおよびCRを引き、CからBSへ垂線CHを下ろす。

接点と中心を結び垂線を下ろす
接線の性質より、BS⊥RS、CR⊥RS
これとBS⊥CHより、CH//RS
よって、CHSRは長方形で、CH=RS=12
△BCHに三平方の定理を用いると、
\(12^2+\mathrm{BH}^2=13^2\)より、BH=5
ここで、β、γの半径をそれぞれ\(b,c\)とおく。

半径を文字でおいて方程式を立てる
中心間の距離について、\(b+c=13\)…(i)
BHについて、\(b-c=5\)…(ii)
(i)と(ii)を解くと、(\(b,c\))=(9, 4)
αについて、中心Aは半径6の円で、周長は\(2\pi × 6\)
これに対し、αの円周は\(2\pi × 3\)
よって、回転数は\(\frac{2\pi × 6}{2\pi × 3}\)=2

内接円の中心が描く軌道
γについて、中心Cは半径13の円で、周長は\(2\pi × 13\)
これに対し、γの円周は\(2\pi × 4\)
よって、回転数は\(\frac{2\pi × 13}{2\pi × 4}\)=\(\frac{13}{4}\)

外接円の中心が描く軌道
これより、回転数の比は\(2:\frac{13}{4}=8:13\)
よって、4が正解である。






コメント
円αの半径が3である根拠は何でしょうか?
与えられた問題文と図では円αの半径は特定出来ないと思うのですが
!!
αの半径3、という条件を入れ忘れておりました。
下半期イチの驚きです。
毎度のご指摘、感謝しております。
今後も何とぞ見守ってくださいませ。