こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
筋トレのあとのプロテインおいしい。
前回は、円形の領域を直線で分割する問題をやりましたね。
今ここで、解法の大まかな流れを思い浮かべてみましょう。
思い出せない方は、早めに復習しておくことをおすすめします。
せっかく苦労して解いた問題を忘れてしまうのは、とてももったいないです。
解いた問題を、まずはしっかりと記憶として定着させましょう。
記憶のストックをコツコツと積み上げることこそ、難しい問題に対応するための近道です!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
次図のように、1つのポンプと水車に対し2つのバルブが直列に接続されている場合、水車が回るのは2つのバルブがともに開いている場合であり、どちらか一方でもバルブが閉まっていれば水は流れず水車は回らない。
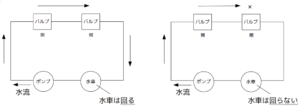
一方、次図のように2つのバルブが並列に接続されている場合は、2つのバルブのうちいずれか片方でも開いていれば水が流れ水車は回るが、2つとも閉まっているときは水が流れず水車は回らない。
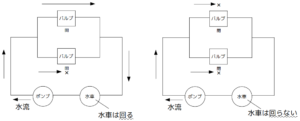
いま、次図のように、\(n\)個のバルブが直列に接続された水道管を用意し、それを\(n\)本並列に接続したAという要素を考える。
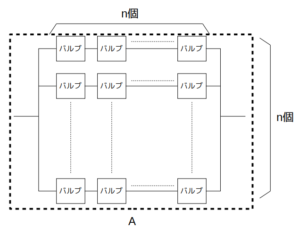
1つのポンプと水車に対し、Aを\(n\)個直列に接続した水路を(ア)、Aを\(n\)個並列に接続した水路を(イ)とする。また、Aを構成するバルブがそれぞれ個別に開いている確率を\(p\)(ただし\(0≦p≦1\))とする。このとき、(ア)で水車が回る確率\(P_ア(n, p)\)、(イ)で水車が回る確率\(P_イ(n, p)\)について、正しい記述はどれか。
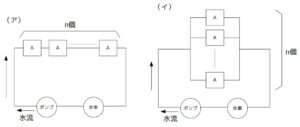
- \(p=\frac{1}{2}\)のとき、\(P_ア=P_イ=\frac{1}{2}\)である。
- \(n=4\)のとき、\(P_イ(4, p)=[1-(1-p^4)^4]^{16}\)である。
- \(p\)が一定のとき、\(n\)が大きくなると\(P_ア\)は大きくなる。
- \(n\)が一定のとき、\(p\)が大きくなると\(P_イ\)は小さくなる。
- \(n\)と\(p\)が一定のとき、\(P_ア(n, p)>P_イ(n, p)\)である。
3
水車とバルブを題材とした、確率の問題ですね。
直列と並列で水車が回る条件が異なることに注意しましょう。
以下で詳しく解説します。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
\(n\)個のバルブが水を「通す」(=水車が回る)確率は、直列ならばバルブが開いている確率\(p\)から直接求められます。
これに対して並列の場合は、「水を通す=少なくとも1つバルブが開いている」なので、余事象である、水を「通さない」確率を経由しなくてはなりません。
このことを頭に入れつつ、まずはA単体が水を通す確率を考えてみましょう。
各バルブが開いている確率は全て\(p\)です。
よって、Aの1列で、\(n\)個のバルブが全て開いていて水を通す確率は\(p^n\)ですね。
これにより、この1列が水を通さない確率は、余事象なので\(1-p^n\)となります。
Aは、これが\(n\)本並列につながっているのですから、Aが水を通さない(=\(n\)本全てが水を通さない)確率は\((1-p^n)^n\)ですね。
これにより、Aが水を通す確率は、余事象なので\(1-(1-p^n)^n\)と求められます。
ここまでを、A単体が水を通す/通さない確率として表にまとめます。
| 通す | 通さない | |
| 確率 | \(1-(1-p^n)^n\) | \((1-p^n)^n\) |
あとは、これが\(n\)個直列になった場合(ア)と並列になった場合(イ)それぞれについて、単体のときと同じやり方で水を通す(=水車が回る)確率\(P_ア\)および\(P_イ\)を求めます。
まず、(ア)についてですが、\(P_ア\)は\(n\)個全てが水を通す確率なので、
表より\(P_ア(n, p)=[1-(1-p^n)^n]^n\)
続いて(イ)ですが、水を「通さない」確率は、\(n\)個のAが全て水を通さない確率なので、
表より\([(1-p^n)^n]^n=(1-p^n)^{n^2}\)
これより、水を「通す」確率は、余事象なので\(P_イ(n, p)=1-(1-p^n)^{n^2}\)
\(P_ア\)と\(P_イ\)が具体的な式として求められましたね。
これらを元に、選択肢の正誤を検討しましょう。
1について
試しに\(p=\frac{1}{2}\)としてみると、\(P_ア(n, \frac{1}{2})=[1-(1-(\frac{1}{2})^n)^n]^n\)
例えば、\(n=2\)のときを考えると、\(P_ア(2, \frac{1}{2})=\frac{49}{256}≠\frac{1}{2}\)
よって、1は誤りです。
2について
\(n=4\)のとき、\(P_イ(4, p)=1-(1-p^4)^{16}\)なので、2は誤りです。
3について
\(p\)が一定のとき、\(n\)が大きくなると\(p^n\)が増えるので\((1-p^n)\)は小さくなります。
すると、\((1-p^n)^n\)も小さくなって\(1-(1-p^n)^n\)は大きくなるので、\([1-(1-p^n)^n]^n\)は増えます。
よって\(p\)が一定のとき、\(n\)が大きくなると、\(P_ア\)は大きくなるので、3は正しいです。
4について
\(n\)が一定のとき、\(p\)が大きくなると\(p^n\)が増えるので\((1-p^n)\)は小さくなります。
すると、\((1-p^n)^{n^2}\)も小さくなって\(1-(1-p^n)^{n^2}\)は大きくなります。
よって\(n\)が一定のとき、\(p\)が大きくなると\(P_イ\)は大きくなるので、4は誤りです。
5について
例えば、\(n=2\)かつ\(p=\frac{1}{2}\)とすると、\(P_ア(2, \frac{1}{2})=\frac{49}{256}\)
また、\(P_イ(2, \frac{1}{2})=\frac{175}{256}>P_ア(2, \frac{1}{2})\)
よって、5は誤りであると分かります。
以上より、3が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
\(n×n\)個のバルブからなる要素を、直列または並列にしたときに水車が回る確率に関する問題でした。
余事象が入れ子状に折り重なっているので、自分が今なんの確率を求めているのか、常にゴールを明確に描く必要がありました。
定式化さえできれば、あとはそれをもとに各選択肢を検討するだけです。
反例は1つあればいいので、\(n\)と\(p\)に具体的な値を入れて調べてもOKです。
例えば4だったら、同じ\(n=1\)に対し、\(p=\frac{1}{2}, \frac{1}{3}\)の2つのケースを比較しても増減は分かります。
本番で自分にあった解き方を選択できるように、普段の勉強ではいろんな解法を貪欲に吸収していく姿勢があるといいですね。
今回は確率の問題としてはやや概念的要素の強い問題でした。
しかし、積の法則や余事象など、やはり根底にあるのは確率の基本的な定理や法則の活用でした。
特に本問は余事象の扱いの練習にはうってつけの教材だったのではないでしょうか。
国家総合職の数的処理では確率分野は頻出なので、幅広いタイプの問題に対応できるよう、トレーニングしていってほしいと思います。
ぜひ本サイトも活用しながら、本番に即した問題演習を繰り返すことで、少しでも数的処理の得点力を上げていきましょう!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
まずAの1列で、\(n\)個のバルブが全て開いていて水を通す確率は\(p^n\)
よってAの1列が水を通さない確率は、余事象であるから\(1-p^n\)
Aはこの1列が\(n\)本並列につながっているから、Aが水を通さない確率は\((1-p^n)^n\)
よって、Aが水を通す確率は、余事象であるから\(1-(1-p^n)^n\)
| 通す | 通さない | |
| 確率 | \(1-(1-p^n)^n\) | \((1-p^n)^n\) |
この結果をもとに、Aが\(n\)個直列の場合(ア)と並列の場合(イ)に水が流れる(=水車が回る)確率を求める。
表より\(P_ア(n, p)=[1-(1-p^n)^n]^n\)
次に、(イ)について、水を「通さない」確率は、\(n\)個のAが全て水を通さない確率で、
表より\([(1-p^n)^n]^n=(1-p^n)^{n^2}\)
これより、水を「通す」確率は、余事象より\(P_イ(n, p)=1-(1-p^n)^{n^2}\)
これら\(P_ア\)と\(P_イ\)を用いて、選択肢の正誤を検討する。
1:×
例えば\(p=\frac{1}{2}\)で\(n=2\)のとき、\(P_ア(2, \frac{1}{2})=\frac{49}{256}≠\frac{1}{2}\)より、誤り。
2:×
\(n=4\)のとき、\(P_イ(4, p)=1-(1-p^4)^{16}\)であり、誤り。
3:○
\(p\)が一定のとき、\(n\)が大きくなると\(p^n\)が大きくなり、\((1-p^n)\)は小さくなる。
すると、\((1-p^n)^n\)も小さくなり、\(1-(1-p^n)^n\)は大きくなるから、\([1-(1-p^n)^n]^n\)は大きくなる。
よって\(p\)が一定のとき、\(n\)が大きくなると\(P_ア\)は大きくなるから、正しい。
4:×
\(n\)が一定のとき、\(p\)が大きくなると\(p^n\)が大きくなり\((1-p^n)\)は小さくなる。
すると、\((1-p^n)^{n^2}\)も小さくなるから、\(1-(1-p^n)^{n^2}\)は大きくなる。
よって\(n\)が一定のとき、\(p\)が大きくなると\(P_イ\)は大きくなるから、誤り。
5:×
例えば、\(n=2\)かつ\(p=\frac{1}{2}\)とすると、\(P_ア(2, \frac{1}{2})=\frac{49}{256}\)
また、\(P_イ(2, \frac{1}{2})=\frac{175}{256}>P_ア(2, \frac{1}{2})\)
よって、誤り。
したがって、正解は3である。

コメント