こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
解いた後すぐに答え合わせができるように、問題の直下に正答番号を表示させるボタンを設置しました。
ネタバレ防止のために、クリックで開く仕様になってます。
ホント、いいねボタンより先にこっちを導入すべきだった。
前回は、果物の階級と購入者の対応関係を推測する問題をやりましたね。
まだ解いてない方は、ぜひ挑戦してみてください。
すでに解いた方は、解いたときのことをここで思い出してみましょう。
どんな問題だったか、どんな解法を使ったか、などなど。
思い出すことで、解法が記憶として定着します。
定着した記憶は、きっと本番で皆さんの力となってくれるはずです。
問題を解いたら、解きっぱなしで終わらず、何度も復習して自分の糧にしましょう。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
あるお店では、パック入りの卵2種類(茶色、白色)を次図のように横一列に並べて置いている。
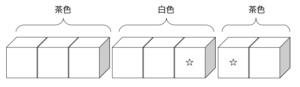
この図において、☆印は値引きされた卵パックであることを示す。
いま、次図の灰色の場所にある卵がすでに購入された状態からスタートして、このお店に来た客が次に示すア〜エの規則にしたがって卵パックを1つずつ選んで購入する場合を考える。
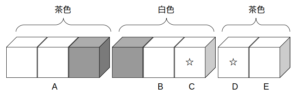
- 可能な限り、値引きされた卵パックを選ぶ。
- 値引きされた卵パックがない場合は、角にあるものを優先して選ぶ。
- 同じ条件に当てはまる同じ色の卵パックが複数ある場合は、等しい確率で1つを選ぶ。
- 同じ条件に当てはまる違う色の卵パックが複数ある場合は、\(\frac{2}{3}\)の確率で白卵を選ぶ。
このとき、白→茶→茶→白の順に購入される確率を最も高くするには、図のA〜Eのうち、どの位置にある卵パックを最初に購入すればよいか。
- A
- B
- C
- D
- E
4
2種類の卵がどんな順番で買われるかは、実際に書き出してみないと分かりませんね。
その意味では、確率分野の中でも場合の数的な要素の強い問題であるといえるかもしれません。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
まずは、A〜Eを最初に選んだ場合のそれぞれについて、卵がどんな順番で買われていくのかを樹形図で書き出してみましょう。
買われる順番が明らかになれば、「白→茶→茶→白の順に購入される確率」も計算できます。
以下では、一番左の1個を「F」として説明します。
優先度の高さは、「値引き」>「角」>「茶 or 白」となります。
例えば、Aが最初に買われた場合に選ばれる順番としてあり得るのは、次の4通りです。
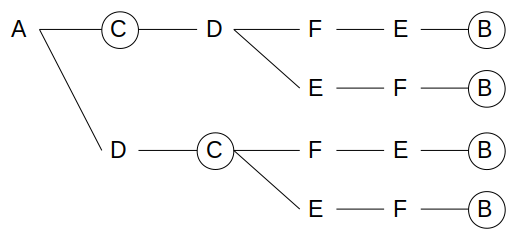
○印は白色の卵です。
このうち、白→茶→茶→白の順に買われるのは下から2つのパターンですね。
これらが起こる確率を求めましょう。
条件エ「同じ条件に当てはまる違う色の卵パックが複数ある場合は、\(\frac{2}{3}\)の確率で白卵を選ぶ」より、最初の分岐でD(茶卵)が選ばれる確率は\(\frac{1}{3}\)です。
次のEとFの分岐では、条件ウ「同じ条件に当てはまる同じ色の卵パックが複数ある場合は、等しい確率で1つを選ぶ」より、EとFのいずれかを選ぶ確率は、どちらも等しく\(\frac{1}{2}\)です。
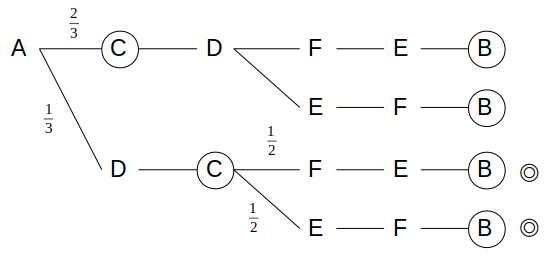
よって、確率は\(\frac{1}{3}×\frac{1}{2}×2=\frac{1}{3}\)
B〜Eを最初に選んだ場合の確率も、同様に調べます。
Bを最初に選んだ場合、買われる順番としてあり得るのは次の4通りです。
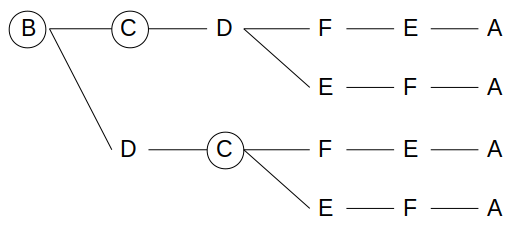
この場合は白→茶→茶→白の順に買われることはないので、確率は0です。
Cを最初に選んだ場合、買われる順番としてあり得るのは次の4通りです。
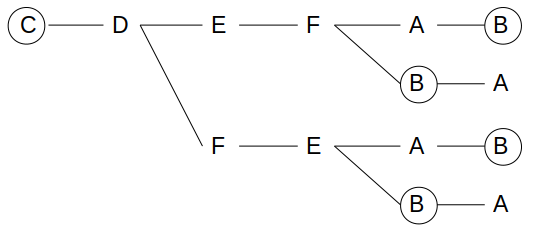
この場合も白→茶→茶→白の順に買われることはなく、確率は0です。
Dを最初に選んだ場合、買われる順番としてあり得るのは次の4通りです。
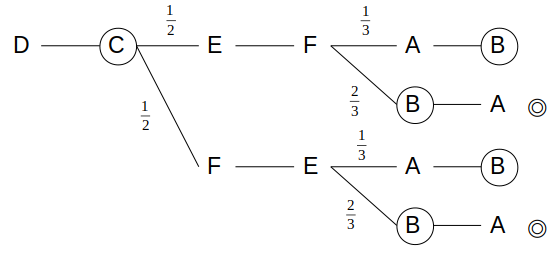
この場合、白→茶→茶→白の順に買われるのは上から2段目と4段目です。
まず、上から2段目のパターンについて、最初の分岐はEとFが選ばれる確率はともに\(\frac{1}{2}\)です。
かつ、2つ目の分岐でBが選ばれる確率は\(\frac{2}{3}\)なので、この場合の確率は\(\frac{1}{2}×\frac{2}{3}=\frac{1}{3}\)
また、上から4段目のパターンについても、同様に\(\frac{1}{2}×\frac{2}{3}=\frac{1}{3}\)です。
これにより、確率は\(\frac{1}{3}+\frac{1}{3}=\frac{2}{3}\)
Eを最初に選んだ場合、買われる順番としてあり得るのは次の4通りです。
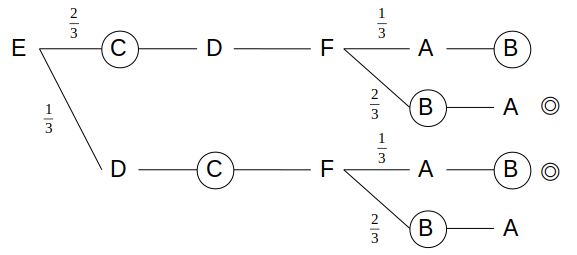
このうち、白→茶→茶→白の順に買われるのは上から2段目と3段目です。
まず上から2段目について、最初の分岐でCを選ぶ確率は\(\frac{2}{3}\)です。
かつ、2つ目の分岐でBを選ぶ確率は\(\frac{2}{3}\)なので、この場合の確率は\(\frac{2}{3}×\frac{2}{3}=\frac{4}{9}\)
また上から4段目については、最初の分岐でDを選ぶ確率は\(\frac{1}{3}\)です。
かつ、2つ目の分岐でAを選ぶ確率は\(\frac{1}{3}\)なので、この場合の確率は\(\frac{1}{3}×\frac{1}{3}=\frac{1}{9}\)
これにより、確率は\(\frac{4}{9}+\frac{1}{9}=\frac{5}{9}\)
以上をまとめると、次のようになります。
| A | B | C | D | E | |
| 確率 | \(\frac{1}{3}\) | \(0\) | \(0\) | \(\frac{2}{3}\) | \(\frac{5}{9}\) |
最も確率が高いのはDなので、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
確率と場合の数は密接な関係にあります。
確率を知るためには場合の数を正確に数え上げなくてはなりません。
樹形図は場合の数を数え上げる方法の一つです。
本問のように、具体的な順番を知りたい問題では有効な手段となります。
書き出す、というのはかなり原始的な方法ですが、数的処理では意外にも有効な場合が多いです。
その場合は数え忘れや重複して数えたりすることがないように注意しましょう。
数的処理の中で、確率は絶対に外せない重要単元です。
もちろん、国家総合職でもかなりの頻出分野となっています。
苦手な方は、まずは書き出して解決できる問題から攻略するのがいいのではと思います。
本サイトで過去に紹介した確率の問題を載せるので、ぜひそちらもチャレンジして、いろいろな出題パターンに触れてみてください↓
もちろん、今後も様々な確率の問題を解説する予定なので、ぜひまた勉強しにきてください!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
一番左の1個を「F」として、A〜Eを最初に選んだときに購入される卵パックの順番を樹形図で書き出したのち、白→茶→茶→白の順番を含む場合が起こる確率を求める。
例えばAを最初に選ぶとき、購入される順番は以下の4通りがあり得る。
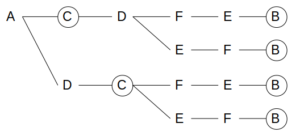
最初にAを選んだ場合に購入される順番
このうち、白→茶→茶→白の順番を含むのは、下半分の2段である。
まず、条件エ「同じ条件に当てはまる違う色の卵パックが複数ある場合は、\(\frac{2}{3}\)の確率で白卵を選ぶ」より、最初の分岐でDが選ばれる確率は\(\frac{1}{3}\)
次の分岐では、条件ウ「同じ条件に当てはまる同じ色の卵パックが複数ある場合は、等しい確率で1つを選ぶ」より、EとFのいずれかを選ぶ確率は、どちらも等しく\(\frac{1}{2}\)
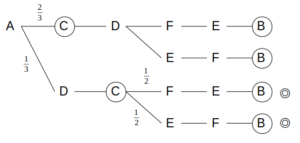
Aの場合の確率
よって、確率は\(\frac{1}{3}×\frac{1}{2}×2=\frac{1}{3}\)
Bを最初に選ぶときは、購入される順番は以下の4通りがあり得る。
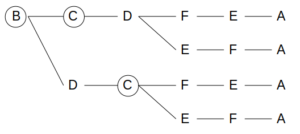
最初にBを選んだ場合に購入される順番
この場合は白→茶→茶→白の順番を含むパターンは起こり得ないので、確率は0である。
Cを最初に選ぶときは、購入される順番は以下の4通りがあり得る。
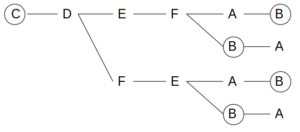
最初にCを選んだ場合に購入される順番
この場合も白→茶→茶→白の順番を含むパターンはないので、確率は0である。
Dを最初に選ぶときは、購入される順番は以下の4通りがあり得る。
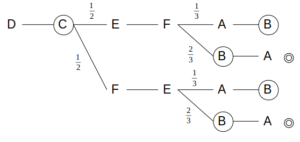
Dの場合の確率
このうち、白→茶→茶→白の順番を含むのは、上から2段目と4段目である。
まず、上から2段目について、最初の分岐でEとFが選ばれる確率はともに\(\frac{1}{2}\)である。
かつ、2つ目の分岐でBが選ばれる確率は\(\frac{2}{3}\)であるから、この場合の確率は\(\frac{1}{2}×\frac{2}{3}=\frac{1}{3}\)
上から4段目のパターンも、同様に\(\frac{1}{2}×\frac{2}{3}=\frac{1}{3}\)
これより、確率は\(\frac{1}{3}+\frac{1}{3}=\frac{2}{3}\)
Eを最初に選ぶときは、購入される順番は以下の4通りがあり得る。
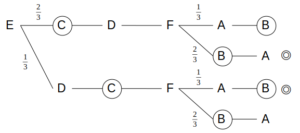
Eの場合の確率
このうち、白→茶→茶→白の順番を含むのは、上から2段目と3段目である。
まず上から2段目について、最初の分岐でCを選ぶ確率は\(\frac{2}{3}\)
かつ、2つ目の分岐でBを選ぶ確率は\(\frac{2}{3}\)であるから、この場合の確率は\(\frac{2}{3}×\frac{2}{3}=\frac{4}{9}\)
上から4段目については、最初の分岐でDを選ぶ確率は\(\frac{1}{3}\)
かつ、2つ目の分岐でAを選ぶ確率は\(\frac{1}{3}\)であるから、この場合の確率は\(\frac{1}{3}×\frac{1}{3}=\frac{1}{9}\)
これにより、確率は\(\frac{4}{9}+\frac{1}{9}=\frac{5}{9}\)
| A | B | C | D | E | |
| 確率 | \(\frac{1}{3}\) | \(0\) | \(0\) | \(\frac{2}{3}\) | \(\frac{5}{9}\) |
以上より、最も確率が高いのはDである。
したがって、正解は4である。

コメント