こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「対応関係」
毎年必ず出題のある、最重要単元。
数的処理は、対応関係をいかに攻略するか、にかかっています。
「対応関係、勉強してるのに過去問が解けない」と困っていませんか?
それもそのはず、巷には対応関係の効果的な解き方が全くと言っていいほど出回っていません。
だから、やみくもに問題を解きまくっても初見の問題には対処できないんです。

その場かぎりの解き方しか載ってないのよね
今回は、数的処理の最難関である国家総合職の試験をパスした筆者が編み出した、対応関係の必勝法ともいえる解き方をご紹介。
本サイトでは、「解法のポイント」として繰り返し紹介しています。
まずは適切なフォーマットを用意すること
- 項目が2つ→○×式
- 項目が3つ→数字など書き込み式
例によって、数的処理の過去問みたいな演習問題を使って学んでいきます。
キーワードは……【表】

過去問を初見で解けるようになりたい人は絶対最後まで見て
演習問題:日帰りツアーの行き先と対応関係
A〜Fは、旅行会社を通じてある県を日帰りで訪れるプランを利用した。このプランでは、朝・昼・夕方の各時間帯に訪れたい場所を選択することができ、場所ごとに滞在時間が決められている。各時間帯に訪れることのできる場所と滞在時間は、下表の通りである。次のことが分かっているとき、確実に正しいといえるのはどれか。
| 朝 | 寺(2h) | 神社(1.5h) |
| 昼 | 海(3h) | 山(3.5h) |
| 夕方 | 博物館(1.5h) | 美術館(1h) |
- A〜Fが1日のうちに訪れた場所の組み合わせは、全員異なっていた。
- A、B、Eが昼に訪れた場所は同じであった。
- BとCが夕方に訪れた場所は同じであり、かつDとEが夕方に訪れた場所も同じであった。
- 1日全体の滞在時間でみると、DとE、AとBとCがそれぞれ同じであった。また、DはA、B、Cのいずれよりも短く、Fよりも長かった。
- Aは朝に神社を訪れた。
- Aは夕方に美術館を訪れた。
- Bは朝に寺を訪れた。
- Cは昼に山を訪れた。
- Dは朝に神社を訪れた。
2
日帰り旅行プランの問題。
選べるっていいよね。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:対応関係の表を作る、樹形図も使って
対応関係の問題っぽい、というのは何となく分かると思います。

条件付きの文章題で位置や順番の話じゃないなら対応関係になる
対応関係といえば……【表】
まずは適切なフォーマットを用意すること
- 項目が2つ→○×式
- 項目が3つ→数字など書き込み式
まずはフォーマット作りから。
【表】に盛り込む項目を、条件&選択肢を見て決めます。
選択肢は、全て「誰(A〜E)」が「いつ(朝昼夕)」に「どこ」を訪れたか、という内容。
項目が3つ、ということで、書き込み式の表にします。
| 朝 | 昼 | 夕 | |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |

「寺or神社」などを書き込んでいきます
合計時間(8通り)を樹形図で書き出す
加えて、条件では「滞在時間」にも触れられています。
合計時間の大小関係なので、合計時間を考える必要があります。
与えられた表によると、滞在時間は訪れた場所の組み合わせで決まります。
例えば、訪れた場所が「寺・海・博物館」の組み合わせだったら、時間は6.5h。
場所の組み合わせは、せいぜい8通り。
であれば、全パターン書き出してもさほど手間はないでしょう。
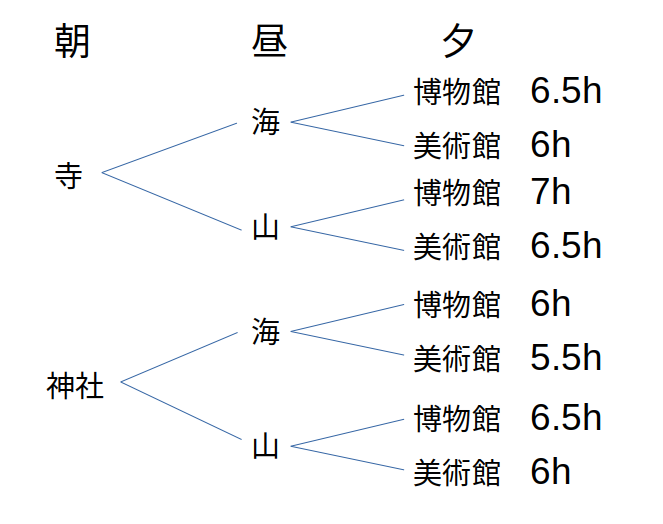
パターン数から時間の対応関係が分かる
さて、
時間の条件1日全体の滞在時間でみると、DとE、AとBとCがそれぞれ同じであった。また、DはA、B、Cのいずれよりも短く、Fよりも長かった。
は「F<D=E<A=B=C」
樹形図によれば、「5.5<6(3)<6.5(3)<7」
大小関係とパターン数から考えて、F=5.5hです。

すると、パターン数の関係からD=E=6h、A=B=C=6.5hに決まります。

DE=6.5だと、またもABC=7になってしまう
D〜Fが訪れた場所の対応関係
樹形図より、F=5.5hの場所は「神社、海、美術館」
| 朝 | 昼 | 夕 | 合計時間 | |
| A | 6.5h | |||
| B | 6.5h | |||
| C | 6.5h | |||
| D | 6h | |||
| E | 6h | |||
| F | 神社 | 海 | 美術館 | 5.5h |
DとE(=6h)は、
3つ目の条件の後半〜、かつDとEが夕に訪れた場所も同じであった。
より、夕の場所が同じ。
樹形図を見ますと、6hで夕の場所が同じである組み合わせは、「寺、海、美術館」と「神社、山、美術館」
すると、候補は次の2パターン。
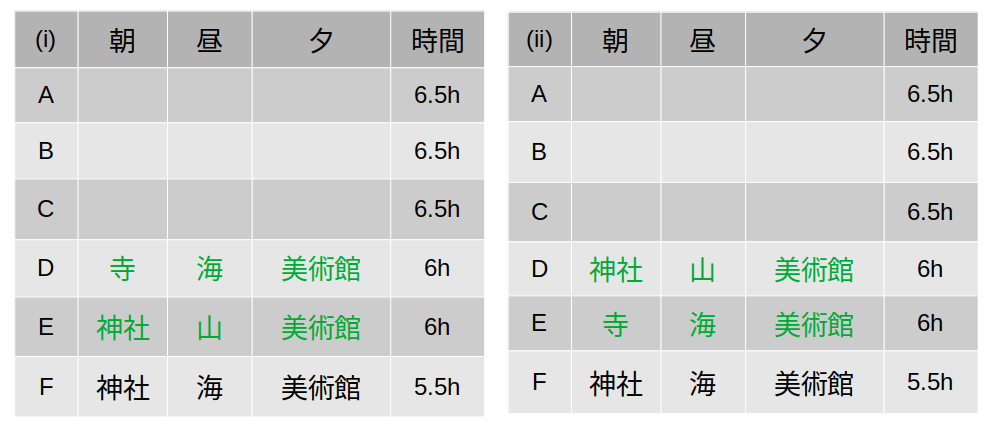

「寺、海、美術館」って美ら海水族館みたいね
(i)→○:滞在時間より対応関係は1通りに決まる
2つ目の条件A、B、Eが昼に訪れた場所は同じであった。 によると、ABの昼は「山」です。
残るは 3つ目の条件の前半BとCが夕に訪れた場所は同じであり、〜 。
BCは、いずれも滞在時間が6.5h。
樹形図を見ると、夕の場所であり得るのは上から「博美博」

これより、BCの夕はともに「博物館」に決まります。

美術館は残り1パターンしかないからB=Cになれない
| 朝 | 昼 | 夕 | 合計時間 | |
| A | 山 | 6.5h | ||
| B | 山 | 博物館 | 6.5h | |
| C | 博物館 | 6.5h | ||
| D | 寺 | 海 | 美術館 | 6h |
| E | 神社 | 山 | 美術館 | 6h |
| F | 神社 | 海 | 美術館 | 5.5h |
Bについて、合計6.5hかつ(昼夕)=(山博)より、Bは「神社、山、博物館」

トリオ解散してそう
すると、昼=山であることより、Aは「寺、山、美術館」
残るCは「寺、海、博物館」に決まります。
| 朝 | 昼 | 夕 | 合計時間 | |
| A | 寺 | 山 | 美術館 | 6.5h |
| B | 神社 | 山 | 博物館 | 6.5h |
| C | 寺 | 海 | 博物館 | 6.5h |
| D | 寺 | 海 | 美術館 | 6h |
| E | 神社 | 山 | 美術館 | 6h |
| F | 神社 | 海 | 美術館 | 5.5h |
(ii)→×:昼A=Bを満たす対応関係はない
この場合、 2つ目の条件A、B、Eが昼に訪れた場所は同じであった。 より、ABの昼は「海」となるはず。
が、樹形図を見てください。
時間6.5hの昼といえば、「海山山」。
つまり、(ii)は条件を満たすことができないので候補から外れます。


「海」になれないって表現、詩的じゃね?
選択肢を検討すると、正しいのは2。
よって、2が正解です。
おわりに:対応関係の表の項目は増えてもOK
お疲れ様でした!
対応関係は【表】です。
選択肢と条件から、必要な項目を読み取り、フォーマットを作ります。
項目の数によって、○×式と書き込み式を使い分けます。
もちろん、最初のフォーマットに必ずしもこだわる必要はありません。
自分にとって分かりやすくなるなら、追記してもOKです。
本問では、しれっと合計時間の列が追加されています。

お分かりいただけただろうか……
対応関係の「解法のポイント」について、詳しく知りたい方はコチラ
もう一問。
もしかして記事タイトル横の「NEW!」って必要ないんじゃね?

毒にも薬にもならない、とはこのこと
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
「誰(A〜E)」が「いつ(朝昼夕)」に「どこ」を訪れたか、を調べるため、次のような表を用意する。
| 朝 | 昼 | 夕 | |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
時間の条件「1日全体の滞在時間でみると、DとE、AとBとCがそれぞれ同じであった。また、DはA、B、Cのいずれよりも短く、Fよりも長かった。」より、滞在時間の合計は「F<D=E<A=B=C」
場所の組み合わせ(8通り)を書き出した樹形図によると、「5.5<6(3)<6.5(3)<7」

樹形図で合計滞在時間を書き出す
大小関係とパターン数から考えて、F=5.5h(神社、海、美術館)
よって、D=E=6h
| 朝 | 昼 | 夕 | 合計時間 | |
| A | 6.5h | |||
| B | 6.5h | |||
| C | 6.5h | |||
| D | 6h | |||
| E | 6h | |||
| F | 神社 | 海 | 美術館 | 5.5h |
樹形図より、合計時間6hかつ夕の場所が同じである組み合わせは、「寺、海、美術館」と「神社、山、美術館」。
よって、あり得るのは次の2通り。

DEの訪れた場所の候補は2パターン
(i)
2つ目の条件「A、B、Eが昼に訪れた場所は同じであった。」によると、ABの昼は「山」。
3つ目の条件の前半「BとCが夕に訪れた場所は同じであり、〜」を考える。
BCは、いずれも合計時間が6.5h。
樹形図より、BCの夕はともに「博物館」となる。

BCの夕の場所は博物館
| 朝 | 昼 | 夕 | 合計時間 | |
| A | 山 | 6.5h | ||
| B | 山 | 博物館 | 6.5h | |
| C | 博物館 | 6.5h | ||
| D | 寺 | 海 | 美術館 | 6h |
| E | 神社 | 山 | 美術館 | 6h |
| F | 神社 | 海 | 美術館 | 5.5h |
Bについて、合計6.5hかつ(昼夕)=(山博)より、Bは「神社、山、博物館」
すると、Aは「寺、山、美術館」、Cは「寺、海、博物館」に決まる。
| 朝 | 昼 | 夕 | 合計時間 | |
| A | 寺 | 山 | 美術館 | 6.5h |
| B | 神社 | 山 | 博物館 | 6.5h |
| C | 寺 | 海 | 博物館 | 6.5h |
| D | 寺 | 海 | 美術館 | 6h |
| E | 神社 | 山 | 美術館 | 6h |
| F | 神社 | 海 | 美術館 | 5.5h |
(ii)
2つ目の条件「A、B、Eが昼に訪れた場所は同じであった。」によれば、ABの昼は「海」。
しかし、樹形図を見ると、時間6.5hあるいは7hである組み合わせで、昼が「海」であるのは1パターンしかないため、このケースは条件を満たさない。

ABの昼の場所は「海」になれない→×
以上より、確実に正しいといえる選択肢は2。
したがって、2が正解である。





コメント
コメント失礼します。
(i)の場合分けについて質問です。
>最終的に、Bの朝が「寺」なのか、「神社」なのかによって2通りが残ります。
ここで2通りの対応関係を提示されていますが、他にもパターンがあるのではないかと思いコメントいたしました。
人:場所(所要時間)として、以下のパターンは存在しないのでしょうか。D、E、Fは解説と同じです。
A:寺(2)、山(3.5)、美術館(1)計6.5
B:神社(1.5)、山(3.5)、博物館(1.5)計6.5
C:寺(2)、山(3.5)、博物館(1.5)計7
もし上記の場合が考えられると、選択肢3.Cは昼に海を訪れた。が確実とは言えなくなります。
私が見当違いなことを言っている可能性が高いのですが、ご確認いただけますと幸いです。
一番乗りですね!
全然見当違いなどではありませんよ
見直したところ、候補は全部で5通りもあったようです
条件「A=B=C」を追加したので、改めて確認してみてください
>A:寺(2)、山(3.5)、美術館(1)計6.5
>B:神社(1.5)、山(3.5)、博物館(1.5)計6.5
>C:寺(2)、山(3.5)、博物館(1.5)計7
「A=B=C」という条件がなければ、このパターンも候補になります
確かにこれだと、Cの昼は確定しませんね
私が解いたところABCの三人のパターンは5通りありました。
そのうちCが山になるケースは2通りあります。
あんぱん小僧さんが挙げた例の他に
A 寺、山、美 6.5h
B 寺、山、博 7h
C 神、山、博 6.5h
があります。
今回も確認ありがとうございました
おっしゃるように、ABCの候補は全部で5通りでした
条件「A=B=C」があれば1通りが残るじゃん、と気づき、問題に少々手を加えました
途中で思い込みが入ると、抜け出せないから恐ろしいですね