こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本ブログ、「数的処理の穴場」を運営しておりますモクセイと申します。
YouTubeの影響で気になっていた、「オートミール」を初めて買って食べてみました。
シンプルに牛乳をかけただけだったんですが、牛乳の甘みとマッチしてかなりおいしかったです。
オートミール自体は味がなくいろんな味付けに合うらしいので、今度はしょっぱい系の味も試してみたいと思います。
オートミールは白米よりも高タンパクだったり、食物繊維が豊富だったりでヘルシーなので、皆さんも毎日の食事に取り入れてみてはどうでしょう?
前回は、4つの小円に外接する大円の内部にできる領域の面積を求める問題をやりましたね。
解法の要点は今ここで思い出せますか?
問題を解いたら、解答のおおまかな流れを時々でいいので思い出してみてください。
数的処理に限らず、勉強した内容は「思い出す」というプロセスによって記憶が強化されます。
「なんとなく覚えてる」くらいのタイミングで復習する方が、完全に忘れてから見返すより効率的に定着させられるのでおすすめです!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
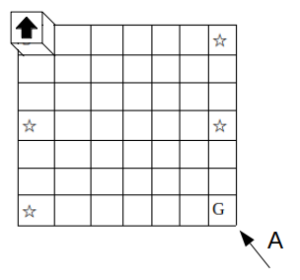
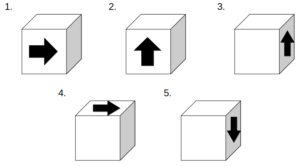
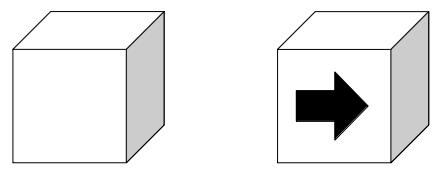
7×7のマス目の左上に、マス目と同じ大きさの側面を持つ立方体を置く。立方体には1つだけ矢印が描かれた面があり、最初、図のようにこの矢印が上向きに見えるように置いてある。いま、この状態からサイコロを振り、以下に示す3つの条件ア〜ウに従って立方体を移動させたところ、サイコロを振る回数が3回で一番右下のゴールのマスGにたどり着いたとする。ゴールにある立方体を図の矢印Aの方向から見たときの見え方としてあり得るのは、次のうちどれか。
- サイコロの目が奇数のときは下に、偶数のときは右に、出た目の数だけ滑らないように立方体を転がして移動させる。
- サイコロを振って移動させるとき、移動先がマス目の範囲を超える場合は移動できず、その場に留まる。
- ☆印のマス目に止まった場合、次の移動のとき、一つ隣のマス目への移動のみ転がさずに滑らせる(2マス目以降は滑らないように転がす)。
1
矢印の付いた立方体を、サイコロの目の数だけ移動させる問題です。
条件に注意して、ゴールにたどり着くまでの経路を、もれなく全て網羅しましょう。
以下で詳しく解説します。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただいても問題ありません。
それではスタート!
詳しい解説
ゴールへたどり着くには、右方向、下方向の移動がともに必須なので、偶数の目も奇数の目も出る必要があります。
また、右方向、下方向の移動がそれぞれ合計で6マスにならなければならないので、3回のうち2回は奇数の目(=下方向の移動)が出る必要があると分かります。
(これにより残りの1回は6の目であると決まります)
和が6となるようなサイコロの目(奇数)の出方は、(1, 5)または(3, 3)しかありません。
よって、この2組について、6の目が何回目に出るのかによって場合分けして考察します。
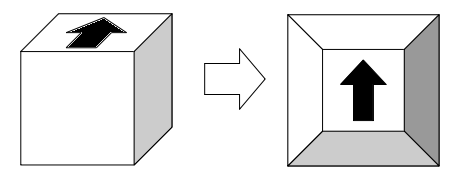
なお、分かりやすさのため、以下では立方体を「位相図」に変換して説明しています。
(位相図が分からない方はこちらの記事の補足の項で詳しく説明してるので、ご参考ください。)
(i)6の目が1回目に出る場合
目の出方は(6, 1, 5)、(6, 5, 1)、(6, 3, 3)のいずれかとなります。
このうち、(6, 1, 5)と(6, 5, 1)では、下方向の移動によって☆印のマスに止まることはないので、立方体の移動のし方はともに次図(左)のようになる。
また(6, 3, 3)では、1回目の「3」で☆印のマスに止まるので、移動のし方は次図(右)のようになる。
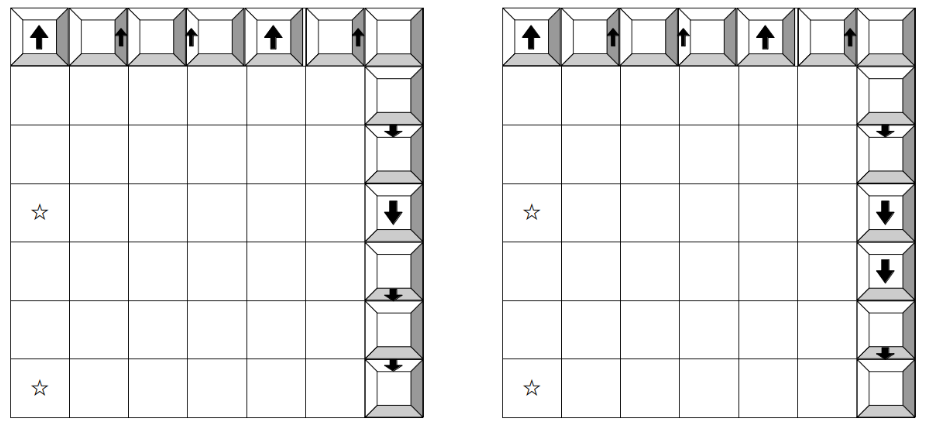
問題文のAの方向から見たとき、結局は両者とも見え方は一緒で、次のようになります。
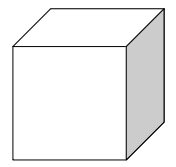
(ii)6の目が2回目に出る場合
目の出方は(1, 6, 5)、(5, 6, 1)、(3, 6, 3)のいずれかです。
このうち、(1, 6, 5)と(5, 6, 1)は、一度も☆印のマスには止まらないので、それぞれ次図(左)の(ii-a)と(ii-b)のように移動します。
また、(3, 6, 3)は2回、☆印のマスに止まるので次図(右)のように移動する。
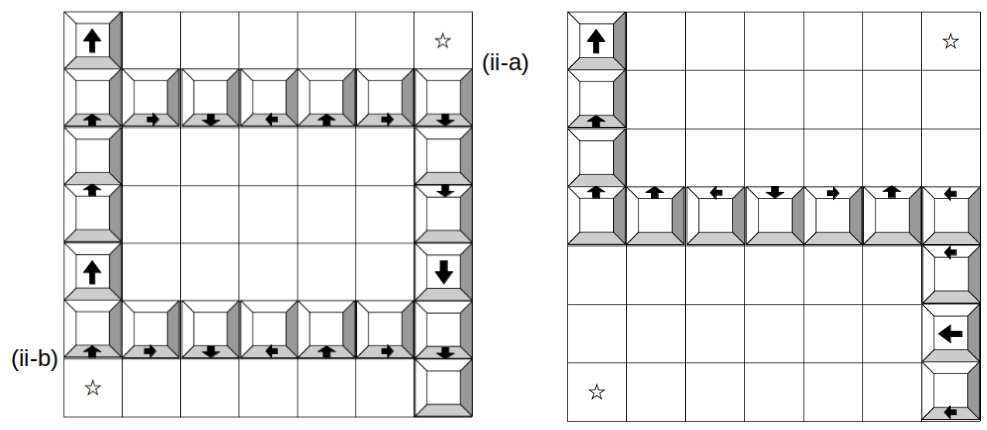
問題文のAの方向から見たときの見え方は、それぞれ次のようになります。
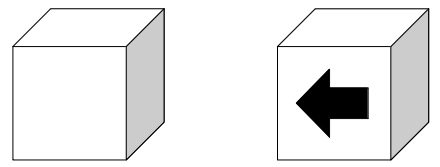
(ii)6の目が3回目に出る場合
目の出方は(1, 5, 6)、(5, 1, 6)、(3, 3, 6)のいずれかです。
このうち、(1, 5, 6)と(5, 1, 6)は、☆印のマスに止まるのは左下のマスの1回のみで、立方体の移動のし方は次図(左)のようになります。
また、(3, 3, 6)の場合は、左下のマスに加え、1回目の「3」のときにも☆印のマスに止まるので、移動のし方は次図(右)のようになります。
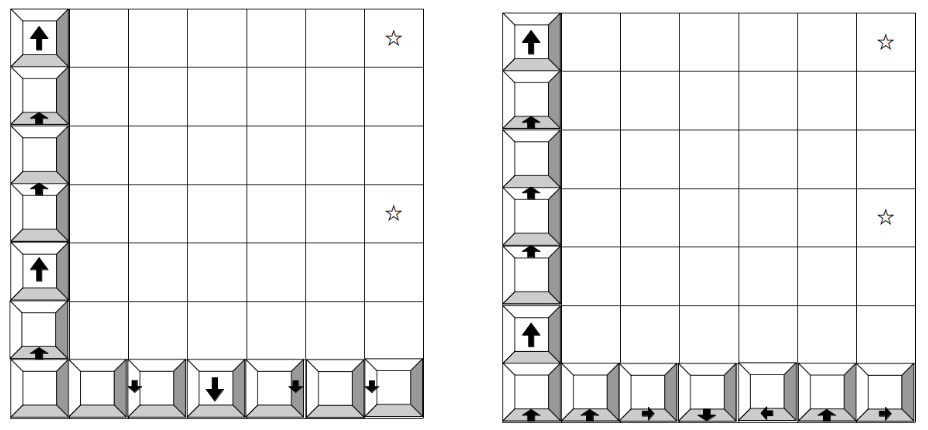
問題文のAの方向から見たときの見え方は、それぞれ次のようになります。
以上より、Aの方向から見た立方体の見え方としてあり得るのは1のみとなります。
したがって、1が正解となります。
おわりに
お疲れ様でした!
いかがだったでしょうか?
サイコロの目の数だけ立方体を移動させる問題でした。
ゴールにたどり着くような目の出方は、(6, 1, 5)あるいは(6, 3, 3)の組み合わせしかないのだ、ということに気づけるかどうかが一つの大きなポイントだったかと思います。
そのことに気づいたら、6の目が何番目に出るのかで場合分けすると見通しが良くなります。
目の順番さえ具体的に決まってしまえば、あとは条件にしたがって立方体を転がすだけですが、ここでも位相図を活用する発想ができると、状況の整理がかなりしやすくなります。
空中で転がすのもアリですが、その場合は正確な空間把握力が問われます。
とはいえ、ただ状況を整理するだけなら、位相図とか使わずとも、自分で分かるような図が描ければそれでOKです。
数的処理では計算過程は問われませんから、あくまで自分用に図で表す方法を持っていれば十分です。
どんな図を描いていいか分からない、という方のために、今回は位相図を使った説明を紹介しました。
国家総合職の数的処理では、今回のように空間を回転させたり展開したり、というような問題は頻繁に出題されています。
毎年1問は必ず空間図形をネタにした出題があるので、避けては通れない分野といえるでしょう。
得意な方は空中で考えるのもアリですが、苦手な方は難しいでしょう。
空間図形に苦手意識がある方は、紙に図を描いて考える練習をしてみてください。
今回使った位相図も、紙(平面)上で思考するための道具の一つなので、ぜひ活用してみてください。
空間図形にも定番の解法は必ずあるので、時間がある方はあきらめずに、まずは簡単な問題から勉強しましょう!
本サイトを通じて少しでも多くの方が苦手を克服し、本番で最高のパフォーマンスを発揮していただければ私もうれしく思います。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
サイコロを振る回数が3回であること、および条件アより、奇数の目が2回、偶数の目が1回出ることが必要である。
さらに、偶数の1回は6の目であり、奇数の2回は(1, 5)または(3, 3)のいずれかである。
以下、6の目が何回目に出るのかによって場合分けする。
目の出方は(6, 1, 5)、(6, 5, 1)、(6, 3, 3)のいずれかである。
このうち、(6, 1, 5)と(6, 5, 1)では、☆印に止まるのは右上のマスの1回のみであるから、立方体の移動は次図(左)のようになる。
また、(6, 3, 3)では、左右の列の真ん中の計2回、☆印のマスに止まるから、右上のマスに加えて右列の真ん中の☆印にも止まるから、立方体の移動は次図(右)のようになる。
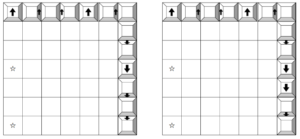
6の目が1回目に出るときの移動
このとき、両者のケースともAから見た立方体の見え方は同じで、次図のようになる。

6が1回目に出るときの見え方
(ii)6の目が2回目に出る場合
目の出方は(1, 6, 5)、(5, 6, 1)、(3, 6, 3)のいずれかである。
このうち、(1, 6, 5)と(5, 6, 1)では、いずれも☆印のマスには止まらないので、立方体はそれぞれ次図(左)の(ii-a)と(ii-b)のように移動する。
また、(3, 6, 3)では、右上のマスに加えて右列の真ん中の☆印にも止まるから、立方体の移動は次図(右)のようになる。
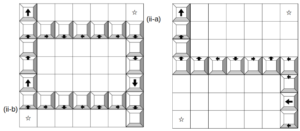
6の目が2回目に出るとき
この場合はAからの立方体の見え方が両者のケースで異なり、それぞれ次図のようになる。
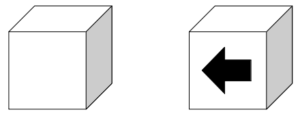
6が2回目に出るときの見え方
(iii)6の目が3回目に出る場合
目の出方は(1, 5, 6)、(5, 1, 6)、(3, 3, 6)のいずれかである。
このうち、(1, 5, 6)と(5, 1, 6)は、☆印のマスに止まるのは左下のマスの1回のみで、立方体の移動は次図(左)のようになる。
また、(3, 3, 6)の場合は、左下のマスに加え、1回目の「3」のときにも左の列の真ん中の☆印に止まるので、立方体の移動は次図(右)のようになる。
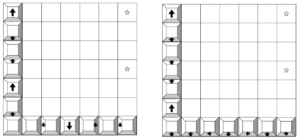
6の目が3回目に出るとき
この場合はAからの立方体の見え方が両者のケースで異なり、それぞれ次図のようになる。
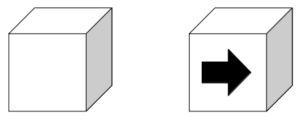
6が3回目に出るときの見え方
以上から、正解は1である。

コメント