こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「方程式」
まずは本サイトの肝である「解法のポイント」を紹介。
これで明日から1点アップ!?
- 未知数を文字でおく
- 数量の関係を式にする
- 連立させて解く
この「解法のポイント」について、詳しく知りたい方は以下の記事をチェック。
ぶっちゃけて言うと、これだけでこの記事の半分はおしまい。
ほら、時間的な感覚だと人生の折り返しは20歳っていうし。

終了、解散!
ここからは、過去問をもとに作ったオリジナルの演習問題を解きながら、「解法のポイント」の使い方を学んでいきます。
演習問題:駅前で配布したチラシの量と方程式
2つの会社AとBが、自社商品をPRするチラシを作成し、甲と乙、2つの駅前で配布した。甲駅では、A社のチラシは全てなくなり、B社のチラシは始めに用意したうちの\(\frac{1}{3}\)が残った。乙駅では、A社のチラシは甲駅と同じ量を、B社のチラシは甲駅の\(\frac{3}{5}\)の量を、それぞれ始めに用意し配布した。その結果、A社のチラシは全てなくなり、B社のチラシは始めに用意したうちの\(\frac{4}{9}\)が残った。駅ごとにみると、甲駅で配布した2社のチラシの総量は乙駅のそれの\(\frac{6}{5}\)倍であった。
このとき、甲駅で始めに用意したチラシの総量に占めるA社の割合に最も近いものは次のうちどれか。
- 30%
- 40%
- 50%
- 60%
- 70%
4
2種類のチラシの割合を求める問題。
選択肢を見ると、何を訊かれてるかが分かり、解き方の方針が立ちます。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:総量の関係を方程式にする
始めに問題の目的(=ゴール)を明確にすることの重要性は、何度かお伝えしています。
目的を意識することで、何をすべきかがハッキリするからです。
本問のゴールは、割合という「数値」を求めること。
数値を求めるのに便利なのが、「方程式」です。
方程式の「解法のポイント」を、いま一度おさらいします。
- 未知数を文字でおく
- 数量の関係を式にする
- 連立させて解く
本問も、これに沿って解いてみます。
甲駅で用意したチラシの量を文字でおく
方程式は、まず未知数を文字でおくことから始まります。
求めたい数値を文字でおくのがキホン。
本問の場合、求める値は割合ですが、これを直接文字でおいても肝心の方程式を立てられません。
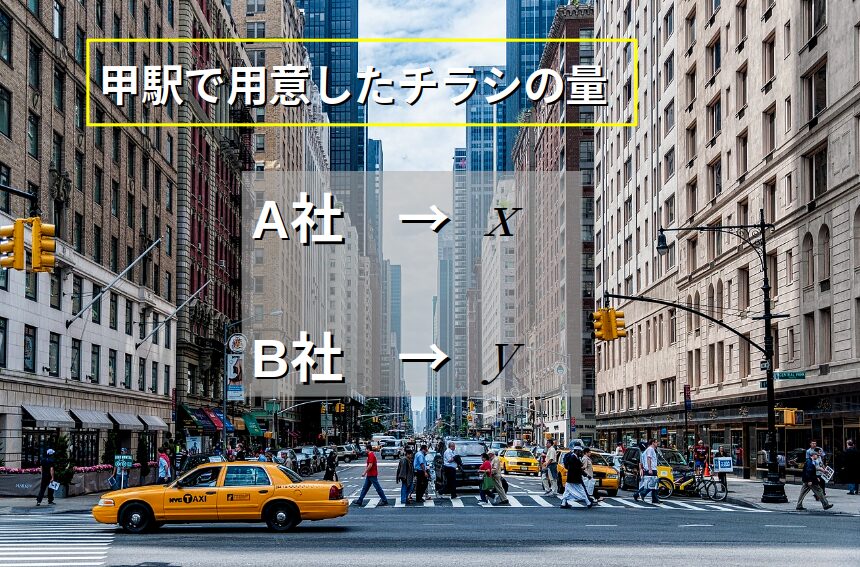
代わりに、甲駅で用意したチラシの量を文字で表します。
A社を\(x\)、B社を\(y\)とします。

求める割合は\(\frac{x}{x+y}\)と表せる
「2駅で配布した総量」を文字式にする
甲駅

A社について
まず、始めに用意した量は\(x\)
「A社のチラシは全てなくなり」とあるので、
残った量は\(0\)
つまり、配布した量は\(x\)
B社について
まず、始めに用意した量は\(y\)
「B社のチラシは始めに用意したうちの\(\frac{1}{3}\)が残った」とあるので、
残った量は\(\frac{1}{3}y\)
つまり、配布した量は\(\frac{2}{3}y\)
よって、甲駅で配布したチラシの総量は、\(x+\frac{2}{3}y\)
| 甲 | A | B |
| 始め | \(x\) | \(y\) |
| 残り | \(0\) | \(\frac{1}{3}y\) |
| 配布量 | \(x\) | \(\frac{2}{3}y\) |
| 総量 | \(x+\frac{2}{3}y\) | |
乙駅

A社について
「A社のチラシは甲駅と同じ量を」用意した、とあるので、
始めに用意した量は\(x\)
そして、「A社のチラシは全てなくなり」とあるので、
残った量は\(0\)
つまり、配布した量は\(x\)
B社について
「B社のチラシは甲駅の\(\frac{3}{5}\)の量を」用意した、とあるので、
始めに用意した量は\(\frac{3}{5}y\)
そして、「B社のチラシは始めに用意したうちの\(\frac{4}{9}\)が残った」ので、
残った量は\(\frac{3}{5}y×\frac{4}{9}\)
つまり、配布した量は\(\frac{3}{5}y×(1-\frac{4}{9})=\frac{1}{3}y\)
よって、乙駅で配布したチラシの総量は、\(x+\frac{1}{3}y\)
| 乙 | A | B |
| 始め | \(x\) | \(\frac{3}{5}y\) |
| 残り | \(0\) | \(\frac{3}{5}y×\frac{4}{9}\) |
| 配布量 | \(x\) | \(\frac{1}{3}y\) |
| 総量 | \(x+\frac{1}{3}y\) | |
「2駅の総量」の関係を方程式に

甲駅および乙駅で配布されたチラシの量について、問題文のラストに言及があります。
“駅ごとにみると、甲駅で配布した2社のチラシの総量は乙駅のそれの\(\frac{6}{5}\)倍であった”
これによると、\((甲の総量)=(乙の総量)×\frac{6}{5}\)
つまり、次式が成り立ちます。
\[
x+\frac{2}{3}y=(x+\frac{1}{3}y)×\frac{6}{5}
\]
整理すると、\(3x=4y\)
つまり、\(y=\frac{3}{4}x\)

ここは\(y=〜\)にすると後々ラク
さて、本問のゴールは「割合」を求めることでした。
\(\frac{x}{x+y}\)に、\(y\)を代入して消去します。
\begin{eqnarray*}
\frac{x}{x+y} &=& \frac{x}{x+\frac{3}{4}x} \\
&=& \frac{4}{7} \\
&≒& 0.57→57\%
\end{eqnarray*}
ここは\(x\)を消去しても解けますが、\(y\)なら代入が1箇所で済みます。

ね、簡単でしょ?
選択肢を検討すると、57%に最も近いのは、4の60%です。
よって、4が正解です。
おわりに:未知数を文字でおき方程式を解く
お疲れ様でした!
方程式の問題は、
【1】文字でおく
【2】方程式を立てる
【3】解く
という3ステップを意識してください。
今回は、駅前で配布したチラシの量にまつわる問題でした。
数値を文字でおいて方程式を立てて解く、という流れは同じ。
未知数2つに対し方程式は1つしかなく、\(x\)と\(y\)を具体的に求めることはできませんが、これでOK。
突き詰めれば、本問で必要なのは「\(x\)と\(y\)の比」という1つの値だからです。
次に示す式変形も参考にしてください。
\[
\frac{x}{x+y}=\frac{1}{1+(\frac{y}{x})}
\]

\(\frac{y}{x}\)を1つの未知数と見なすってこと
がっつりPRADA写ってる画像あるけど怒られませんように

親がPRADA社員で公務員志望の人いたら見逃して
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
甲駅で始めに用意したチラシの量について、A社を\(x\)、B社を\(y\)とする。
甲駅
A社について、始めに用意した量は\(x\)
「A社のチラシは全てなくなり」より、残った量は\(0\)
→配布した量は\(x\)
B社について、始めに用意した量は\(y\)
「B社のチラシは始めに用意したうちの\(\frac{1}{3}\)が残った」より、
残った量は\(\frac{1}{3}y\)
→配布した量は\(\frac{2}{3}y\)
よって、甲駅で配布したチラシの総量は、\(x+\frac{2}{3}y\)
乙駅
A社について、始めに用意した量は\(x\)
「A社のチラシは全てなくなり」より、残った量は\(0\)
→配布した量は\(x\)
B社について、始めに用意した量は\(\frac{3}{5}y\)
「B社のチラシは始めに用意したうちの\(\frac{4}{9}\)が残った」より、
残った量は\(\frac{3}{5}y×\frac{4}{9}\)
→配布した量は\(\frac{3}{5}y×(1-\frac{4}{9})=\frac{1}{3}y\)
よって、乙駅で配布したチラシの総量は、\(x+\frac{1}{3}y\)
ここで、「駅ごとにみると、甲駅で配布した2社のチラシの総量は乙駅のそれの\(\frac{6}{5}\)倍であった」より、次式が成り立つ。
\[
x+\frac{2}{3}y=(x+\frac{1}{3}y)×\frac{6}{5}
\]
つまり、\(y=\frac{3}{4}x\)
これを、\(\frac{x}{x+y}\)に代入し消去すると、
\begin{eqnarray*}
\frac{x}{x+y} &=& \frac{x}{x+\frac{3}{4}x} \\
&=& \frac{4}{7} \\
&≒& 0.57→57\%
\end{eqnarray*}
57%に最も近いのは、4の60%である。
よって、4が正解である。





コメント
「2駅で配布したチラシの総量でみると、A社はB社の6/5であった。」という文章は
2駅でのA社のチラシの配布量が2駅でのB社のチラシの配布量の6/5倍、という意味になると思うのですが…
つまり式で表現すると 2X=Y×(6/5)
整理すると 5X=3Y、X:Y=3:5 でこれを元にすると 答えは X/(X+Y)=0.375 で2番になります
(甲の総量)=(乙の総量)×(6/5) という式を成立させるのなら文章は
「それぞれの駅での二社あわせた配布量は、甲駅は乙駅の6/5倍であった。」にすべきかと思います
おっしゃること、まさにその通りです。
意図していたのは「駅ごとの配布量」で、甲駅の配布量が乙駅の5/6倍、ということでした。
「A社はB社の6/5倍」だったら、前半の考察が全く無意味になりますね。
もしそんな問題を書く人間がいたら、顔が見たいですよ。