- 面積問題の解法パターンが分かる
- 今日から使える面積問題の解法が身につく
- 過去問の類題を例に、本番で役立つ「解法のポイント」の使い方を学べる
- どこよりも詳しい解説で、本試験レベルの問題を完全理解
→数的処理の図形分野に強くなる!
こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
【急募】Twitterで発信するネタがない
数的処理で図形分野からの出題が全くない年はありません。
とりわけ、数的処理で合格点を狙うなら、面積の問題の対策は必須といえます。
なぜなら……
- 図形分野で面積を扱った問題はかなり多い
- 計算が比較的単純でミスによる失点が少ない
そんな面積の問題に、典型的な解法のパターンがあるとしたら、とてもありがたいしぜひ知りたいですよね。
この記事では、公務員試験の数的処理で頻出の面積を求める問題について、まずはじめに2つの解法パターンを紹介します。
それから過去問の類題を一緒に解いて理解していただくことで、本番で使える解法を身につけていってもらいます!
講義:面積の求め方2パターン
面積の求め方は、次の2パターンを知っておけばOKです。
- 大きさが分かっている図形との相似比から求める方法
- 具体的に長さを求めて面積公式に当てはめる方法
【1】大きさが分かっている図形との相似比から求める方法
面積比は相似比と等価なので、実質的に相似比を求める方法になります。

三角形であれば底辺や高さの比に持ち込むパターンもあるよ
図形を分割したり、角の二等分線を引く、などして比を求めます。
「〜の面積(or 辺の長さ)を1とすると…」とか「何倍か?」という表現があったら、このやり方で解決できる可能性があります。
(例題)
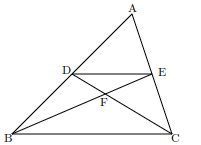
AD:DB=AE:EC=1:1, DF:FC=EF:FB=1:2である。
①面積比△DFE:△DFBを求めよ。
② 面積比△ADE:△DBEを求めよ。
③面積比△DFE:△ABCを求めよ。
(答)
面積比 – 中学校数学・学習サイト
① EF:FB=1:2なので
△DFE:△DFB=1:2
② AD:DB=1:1なので
△ADE:△DBE=1:1
③ △DEF=1とすると△DFB=2、
△DBE=3なるので△ADE=3
△ABE=6になるので△CBE=6
すると△ABC=12
よって△DFE:△ABC=1:12
【2】具体的に長さを求めて面積公式に当てはめる方法
必要な材料をそろえて公式に当てはめる方法です。
求めたい図形が特徴的な形(直角三角形とか台形とか平行四辺形とか)をしていたら、こちらの方法を検討してみてください。

三角形なら底辺×高さ÷2、台形なら(上底+下底)×高さ÷2だね
この方法では、図形の辺の長さを具体的に求めるのが目標となります。
直角三角形があれば、三平方の定理や辺の比が使えます。
(例題)
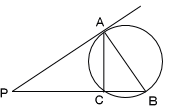
左の図で、ABは円の直径、PAは円の接線、点C はPBと円との交点です。AB=4cm、PA=12cm であるとき、次の値を答えてください。
(1) CAの長さ
(2) △AC Bの面積 (日本大豊山女子高)
(答)
(1)接線と直径の接点において、∠PAB=90°
180°の円周角は、∠AC B=90°
三平方の定理から、PBを求める。
相似な直角三角形の辺の比から高さを求める。
PB=\(\sqrt{({12}^2+{4}^2)}\)=\(4\sqrt{10}\)
△BPA∽△BAC なので、
\(4\sqrt{10}\):12=4:CA
CA=\(\frac{6\sqrt{10}}{5}\)(cm) ・・・(答)(2)CB=\(\sqrt{({4}^2+{CA}^2)}\)
接線・内接円と面積 | 中学から数学だいすき!
=\(\frac{4}{\sqrt{10}}\)
よって、
△ACB=\(\frac{4}{\sqrt{10}} \times \frac{12}{\sqrt{10}} \times \frac{1}{2}\)
=\(\frac{12}{5}\) (cm2)
以上の講義を踏まえて、演習問題に行ってみよう!
演習問題:三角形の内分点と面積比
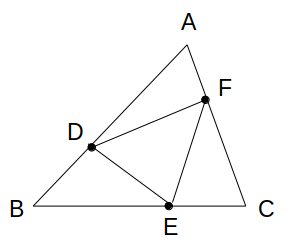
図のように、△ABCの辺AB、BC、CAを2:1に内分する点をそれぞれD、E、Fとするとき、△DEFは△ABCの何倍か。
- \(\frac{2}{9}\)倍
- \(\frac{1}{3}\)倍
- \(\frac{3}{7}\)倍
- \(\frac{4}{9}\)倍
- \(\frac{3}{5}\)倍
2
三角形の内分点と面積比の問題です。
面積の問題の対処法は2パターンしかないことを思い出しましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
- 大きさが分かっている図形との比から求める方法
- 具体的に長さを求めて面積公式に当てはめる方法
本問では辺の長さが具体的に与えられていません。
しかも、本問の主旨は「△ABCと△DEFの面積比を求めよ」ということです。

問題文に「何倍か?」という表現があるよ
これらのことから、今回は1の方針が適切であると判断できます。
△ABCと△CEFの面積比は?

図のように、点AおよびFから辺BCへ下ろした垂線の足をそれぞれP、Qとします。
AP//FQなので、△ACP∽△FCQ
これより、AP:FQ=3:2
これは△ABCの高さと△CEFの高さの比が\(1:\frac{2}{3}\)であることと同義です。
さらに、BC:CP=3:1なので、△ABCの底辺と△CEFの底辺の比は\(1:\frac{1}{3}\)です。

底辺と高さがそれぞれ\(\frac{1}{3}\)倍と\(\frac{2}{3}\)倍だから、△CEFは\(\frac{1}{3} \times \frac{2}{3}\)倍だ!
このことより、△ABC:△CEF=\(1:\frac{2}{3}×\frac{1}{3}\)=\(1:\frac{2}{9}\)
全体から余計な部分を除く
同様の手順によって、△ABC:△ADF=\(1:\frac{2}{9}\)が示されます。
同じく、△ABC:△BDE=\(1:\frac{2}{9}\)です。
ゆえに、△DEF=△ABC−(△ADF+△BDE+△CEF)=\(\frac{1}{3}\)△ABC
よって、2が正解です。
別解:三角比の面積公式による方法
「解法のポイント」の2を使った解き方もあります。
三角形の面積公式には、三角比を使ったものがありました。

\(△\mathrm{ABC}=\frac{1}{2}\mathrm{AB}×\mathrm{AC}\sin \angle\mathrm{A} \)ってやつね
「三角形の面積は、2辺とその間の角度を用いて表される」というものでしたね。
これによれば、角度が共通な三角形の面積比は、はさむ2辺の比に等しいことになります。
例えば本問の場合、△ABCと△ADFは∠Aが共通なので、∠Aをはさむ2辺の長さの比から面積比を知ることができます。
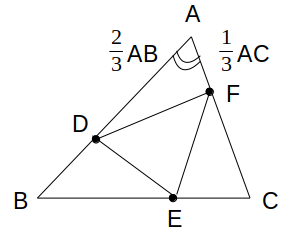
\begin{eqnarray}
△\mathrm{ADF} &=& \frac{1}{2}\mathrm{AD}×\mathrm{AF}\sin \angle\mathrm{A} \\
&=&\frac{1}{2}×\frac{2}{3}\mathrm{AB}×\frac{1}{3}\mathrm{AC}\sin \angle\mathrm{A} \\
&=&\frac{2}{9}\left(\frac{1}{2}\mathrm{AB}×\mathrm{AC}\sin \angle\mathrm{A}\right) \\
&=&\frac{2}{9}△\mathrm{ABC}
\end{eqnarray}
全く同様の手順により、△BDE=△CEF=\(\frac{2}{9}\)△ABCを知ることができます。
△DEF=△ABC−(△ADF+△BDE+△CEF)=\(\frac{1}{3}\)△ABCより、2が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
面積の問題は、もとの図形との相似比か面積公式で解けます。
今回は、三角形の内分点を頂点とする三角形と面積比に関する問題でした。
何度も言いますが、面積の問題を見たら、まずは公式か相似比か、いずれを使って解く問題なのかを判断するのが大切です。
前回やった公式を使うパターンに対し、今回は相似比を使うパターンでした。
面積の解法2パターンは、絶対暗記してください。
知っているだけで心強いですし、実際に得点率も上がるはず。
小学校で習う底辺と高さの面積公式を用いた解法に加え、別解として高校数学で習う三角比を使った面積公式による解法を紹介しました。
前者は中学生でも理解できる解法ですが、数学が得意な方には、むしろ別解の方が分かりやすく感じられるかもしれません。
どちらでも、ご自分が理解しやすいやり方を身に付けてください。

筆者は別解の方がかな
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解

△ABCと△CEFの面積比を求める
図のように、点AおよびFから辺BCへ下ろした垂線の足をそれぞれP、Qとする。
△ACP∽△FCQより、AP:FQ=3:2
また、BC:CP=3:1
よって、△ABC:△CEF=\(1:\frac{2}{3}×\frac{1}{3}\)=\(1:\frac{2}{9}\)
同様にして、△ADF=△BDE=△CEF=\(\frac{2}{9}\)△ABC
これより、△DEF=△ABC−(△ADF+△BDE+△CEF)=\(\frac{1}{3}\)△ABC
したがって、2が正解である。

コメント
頭がカタイですね。解らないが,判らないのが分かって脳の機能不全がわかりました。数学の問題は大好きです!
コメントありがとうございます!
多くの人が読んで分かるような解説を作れるように精進します。
よかったら他の問題も見て、楽しんでいってくださいね。
問題文の内容を見ると、答案選択肢の主旨に合っていないと思われます。
「△ABCは△DEFの何倍か?」ではなく
「△DEFは△ABCの何倍か?」
であると思いますがいかがでしょうか?
コメントありがとうございます。
てにおはが間違っており、失礼しました。
おっしゃる通り、「△DEFは△ABCの何倍か?」というのが本問の主旨になります。
ご指摘感謝いたします。
ぜひ他の問題も見ていってくださいね。
何か気づいたことなどあれば、遠慮なくコメントください!