こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「対応関係」
「対応関係は表で解く!!」
本サイトでは、表を使った対応関係の解き方を繰り返しお伝えしています。
対応関係の問題を解いてて、こんなことはありませんか?
これらのお悩みは、【場合分け】を習得することで解決できるかもしれません。
せっかく表を作れるようになったのに、得点に結びつかないのはオシイ。
今回も、数的処理の過去問みたいな対応関係の問題を、どこよりも丁寧に解説していきます。
演習問題:スポーツ大会の対応関係
あるスポーツ大会の参加者は、事前のアンケートで5つの種目(ソフトボール、サッカー、テニス、バレーボール、バドミントン)から2種目を選んで回答し、いずれか一方の選手として出場する。ある回の参加者A~Eについて、次のことが分かっているとき、確実に正しいといえるのはどれか。
ただし、A~Eはいずれもただ1種目の選手として出場したものとする。
- 2人以上が選んだ種目は、全5種目のうちに4種目あった。
- Aは、Dと同じ2種目を選んで回答した。
- Bはテニスとバドミントンを選んで回答した。
- Cはサッカーを選んで回答したが、選手にならなかった。
- Dはテニスの選手となった。
- Eが選んで回答した2種目について、一方はBと、もう一方はCと一致していた。
- Aはバレーボールの選手であった。
- Cはソフトボールの選手であった。
- Dはソフトボールとテニスを選んで回答した。
- Eはサッカーとバドミントンを選んで回答した。
- バレーボールを選んだのは1人だけであった。
4
「何を聞かれているのか?」をハッキリさせると、方針が立ちます。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:A~Eと種目の対応関係
条件をもとに正しい記述を選ぶ、典型的な文章題の形。
しかも、位置や順番の話ではないことから、対応関係の問題だと判断できます。
対応関係といえば、おなじみの【表】
まずは適切なフォーマットを用意すること
- 項目が2つ→○×式
- 項目が3つ→数字など書き込み式
表にする項目は、条件と選択肢から決まります。
次のフォーマットに、〇×を書き入れます。
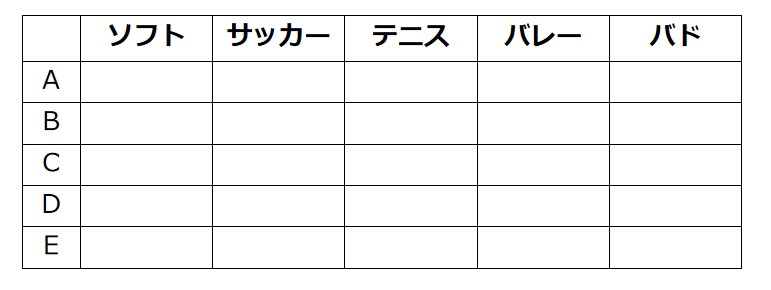
条件を対応関係の表に記入
条件を読み、分かることを記入してしまいましょう。
以下はそのまま書き込めます。
- Bはテニスとバドミントンを選んで回答した。
- Cはサッカーを選んで回答したが、選手にならなかった。
- Dはテニスの選手となった。
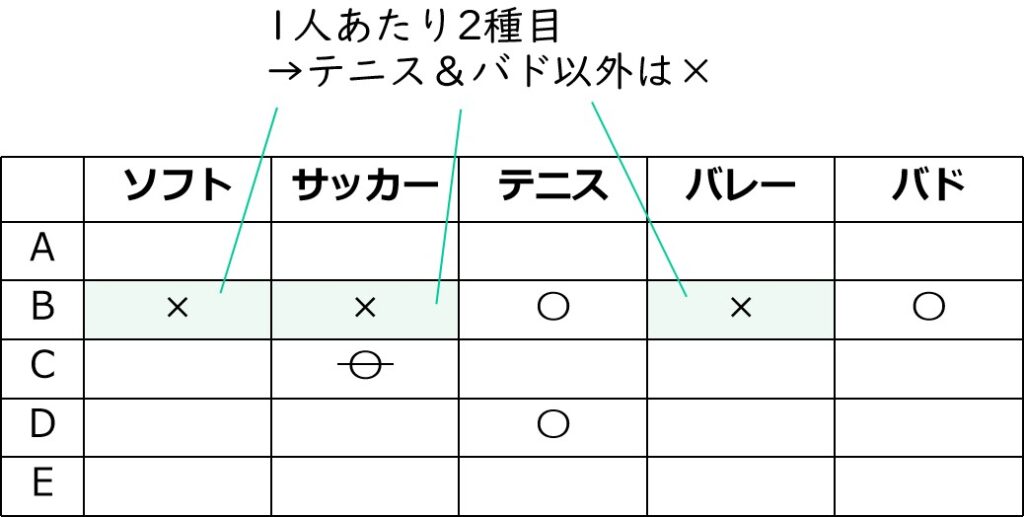
選ぶ/選ばないが〇×に対応します。

選んだけど選手じゃない→取り消し線をチョイ足し
ついでに、2つ目の条件「Aは、Dと同じ2種目を選んで回答した。」より、Aのテニスも〇。
(テニスはDなので、Aは選手じゃない)
ついでにBもテニスは×。
→Bはバドミントンの選手(消去法)
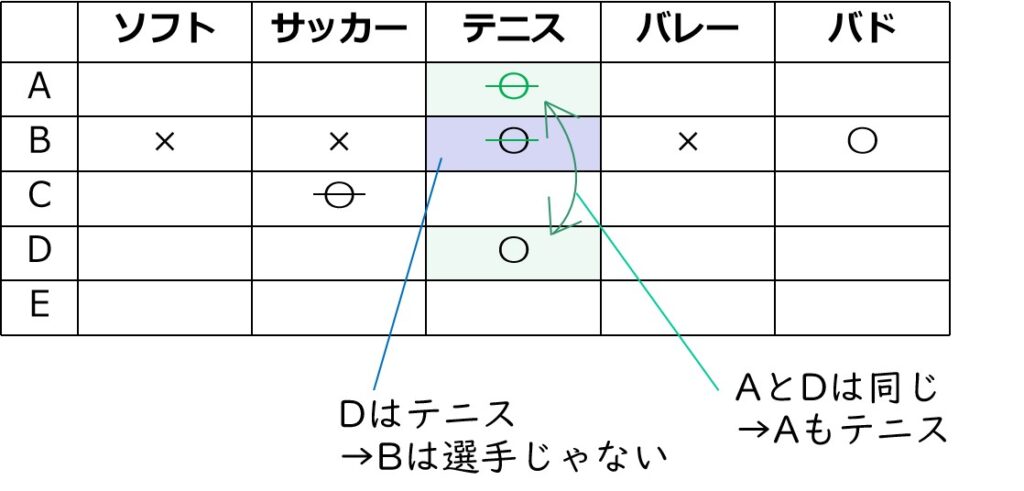
種目を選んだ人数の条件を考える
あと手つかずなのは、最初と最後の条件。
このうち、最後のヤツの方はまだ使えないので後回し。

Bはどっちか不明、Cは2つ目が決まってない
カギを握るは、最初の条件。
- 2人以上が選んだ種目は、全5種目のうちに4種目あった。
言い換えると、「1人だけが選んだ種目が1種目あった」ということ。
1人あたり2票×5人=10票を5種目に振り分けるなら、得票の内訳は次のようになるはず。

1人だけ&3人が1種目ずつ、残りは2人
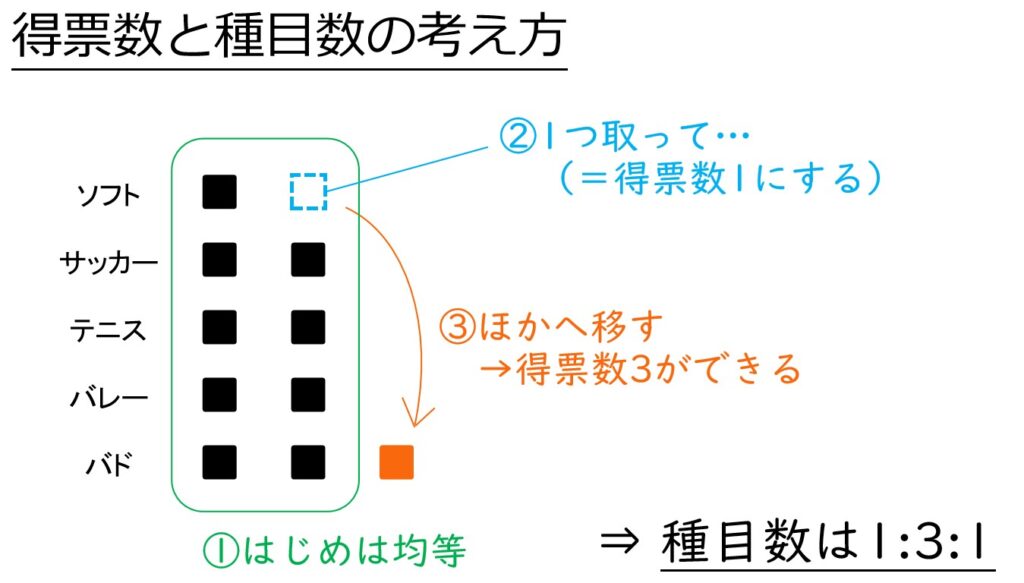
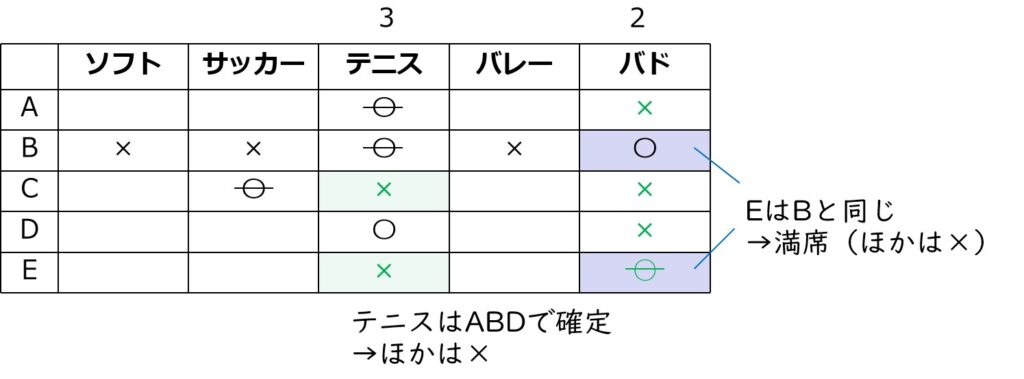
表より、3人が選んだ種目はテニス。
ほかの種目は2人以下なので、Eはバドミントンを選んで選手になったことになります。

EはBと同じ→テニスは満席→バド
これでバドミントンは満席。
→列に残った空白は全て×
Cの種目で場合分け
条件だけで解き明かせるのはここまで。
先へ進むためには、ある程度の決め打ちも必要。
つまり、、、【場合分け】

ときには起こせよムーブメント(訳:自分から動け)
して、何を決め打ちしましょう?
Cに注目。
確定済みのBをのぞく4人のうち、Cだけは残り1種目が二つに一つ。
以下、Cのもう一方が(i)ソフトボール、あるいは(ii)バレーボールの場合に分けます。
(i)Cがソフトボールの場合
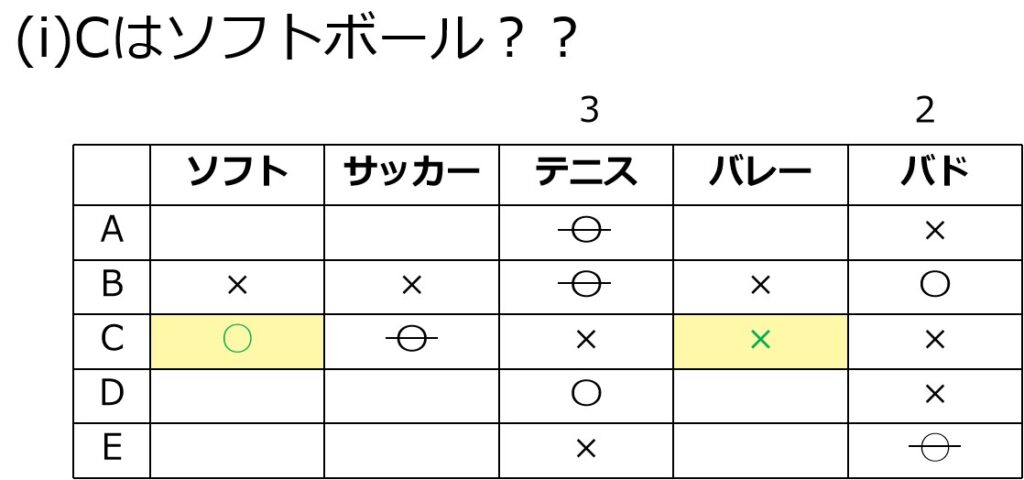
Cといえば、E。
CとEは、
最後の条件Eが選んで回答した2種目のうち、一方はBと、もう一方はCと一致していた。
により関連付けられていたことを思い出します。
一方が決まればもう一方も決まる、一蓮托生の関係。

一蓮托生[名]結果によらず行動や運命を共有すること。プリキュア。
条件によれば、Eはソフトボール or サッカーを選んでいます。
かりにソフトボールだったとしてみますと、、、
Cはソフトボールの選手なので、Eは選手ではありません。
Eがバドミントンの選手じゃなかったことと合わせると、Eは選んだ2種目とも選手でなかったことになり、前提条件に反します。
→Eが選んだのはサッカー
サッカーはこれにて満席。(残る得票数は1か2)
→サッカーの選手はE

ついでに、Eのソフトとバレーは×ね
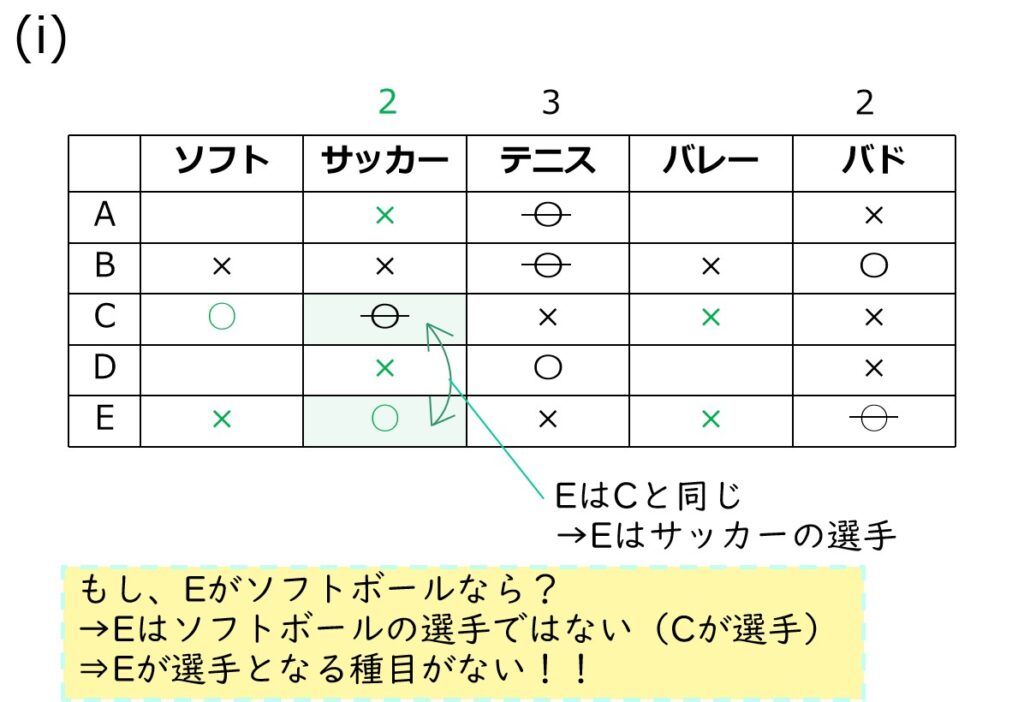
残るは、A&Dのもう1種目。
条件より、あり得るのは「両者ともソフトボール」 or 「両者ともバレーボール」
前者はソフトボールが3人になってしまうのでNG。
→A&Dはバレーボール

Dはテニスの選手→バレーボール選手はA
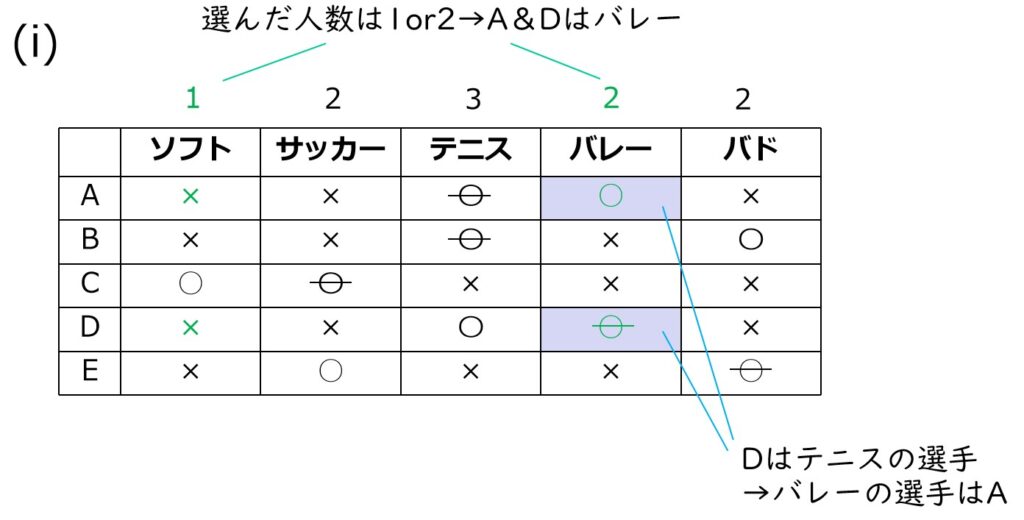
(ii)Cがバレーボールの場合
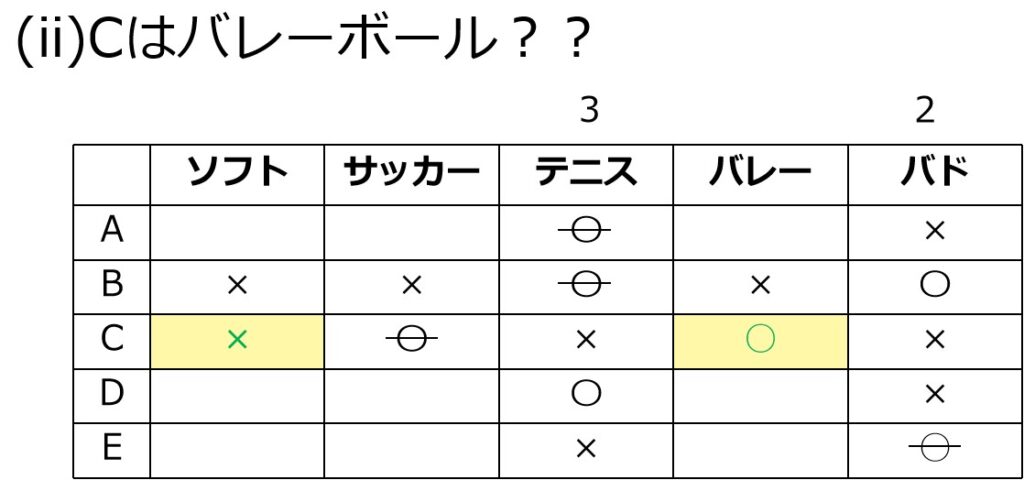
条件「A=D」により、A&Dのもう1種目が決まります。
(何だろ?楽しみだな~)

次回、『AとD、ソフトボール』
↑ネタバレしてくるタイプの次回予告
サッカーもバレーボールも、すでにCで1人確定しています。
ADが選んだ場合、計3人が選んだことになり、得票配分の条件に合わなくなります。
(選んだ人数は1 or 2人だったはず)
→A&Dはソフトボール
さらに、どちらか一方はソフトボールの選手。
Dはテニスの選手なので、Aがソフトボールの選手となるしかありません。
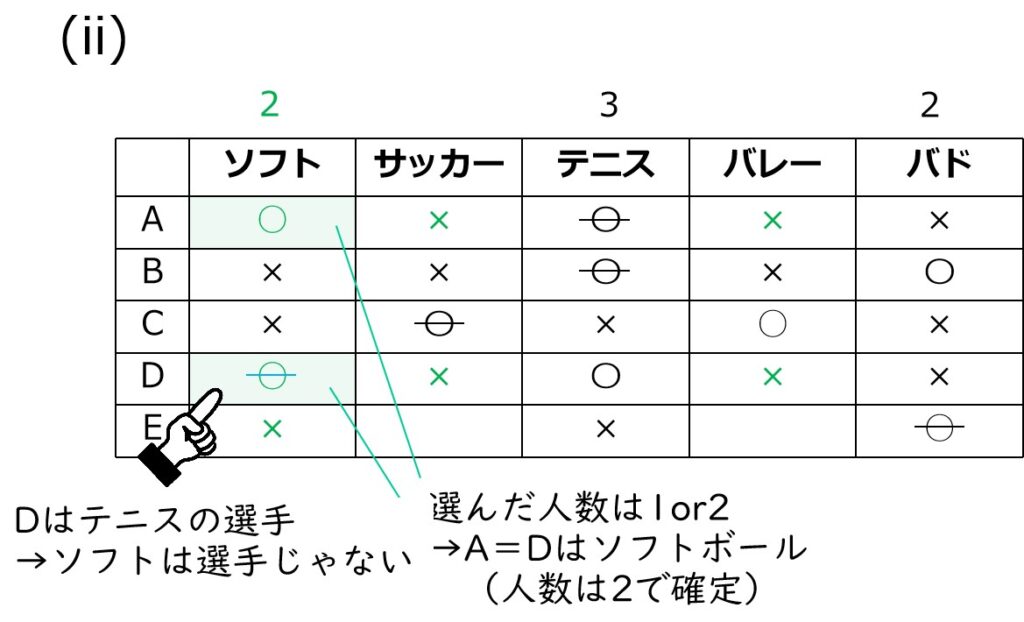

A&Dの横列とソフトボールの縦列は×で埋める
残るはE。
Eがサッカーなのかバレーボールなのかは、得票配分から決まります。
得票配分の条件によれば、一方は1人だけが選んだ種目。
仮にEがバレーだったとしますと、Eは選手ではないことになります。(Cがバレー選手)
→Eはサッカー(かつ選手)
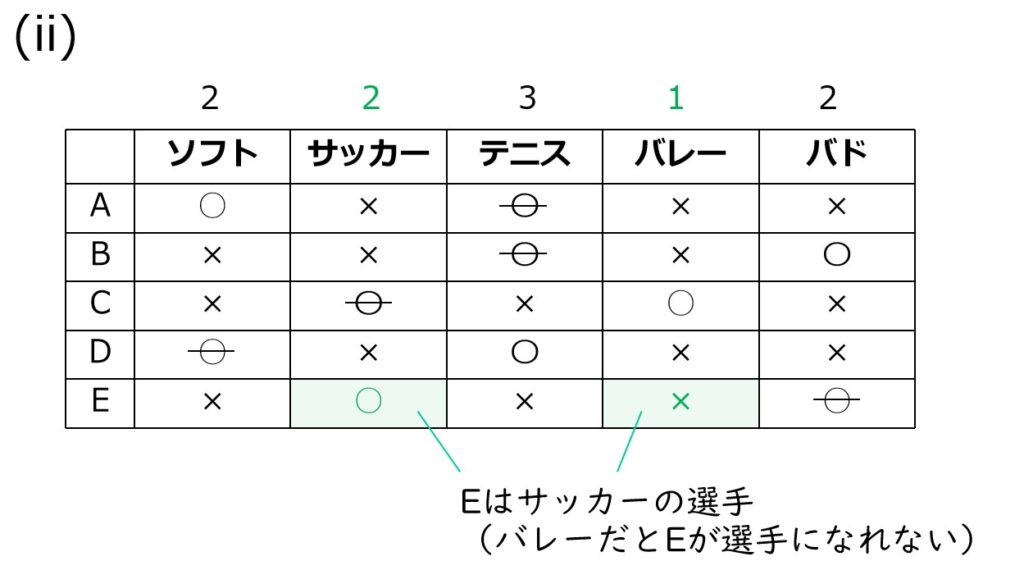
さて、(i)と(ii)の表をもとに選択肢を検討しますと…
正しいのは4。


よって、4が正解です。
おわりに:“場合分け”が対応関係の分水嶺
お疲れ様でした!
対応関係は、表で解く…
そんな時代は、もう終わる ※終わりません
対応関係の攻略に、【場合分け】の習得は不可欠。
表を作り方を覚えたら、こちらもマスターしてください。
枝分かれを少なく、がコツですよ。
本問は、条件を表に落とし込んでいくと、Cの種目が2通りにまで絞られます。
Cの種目で場合分けし、表を完成させます。
ちなみに(i)は「A=D」を先に特定しても解けます。
最後の見直してて「そっちのが早いんじゃね?」って気づきました。
以下、関連記事。
↓やさしめ
↓むずかしめ
goo、辞書やめるってよ。

長い間!!!たまにお世話になりました!!!
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!





コメント