こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、カラオケ大会の賞金を山分けする問題でした。
平易ながら、数的処理で大切な「最初の一手」の考え方を学べる内容です。
ぜひ解いてみてください。
もう解いた方は、お疲れ様でした。
勉強したことを定着させるためにも、復習をやってほしい。
もっと言うと、「解法の一般化」をやってほしい。
学んだ解法から、目の前の問題だけでなく、似たタイプの問題にも使えそうな要素を抽出してインプットする、というやり方です。
闇雲に解法を丸暗記しても、なかなか得点には結びつきにくいというのが実情です。
過去問は予想問題ではないので、全く同じ内容が出題されることはほぼありません。
だからこそ、問題演習では他の似た問題に活用することを前提に学ぶ必要があります。
本サイトなら、「解法のポイント」を覚えるだけでも効果はありますよ!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
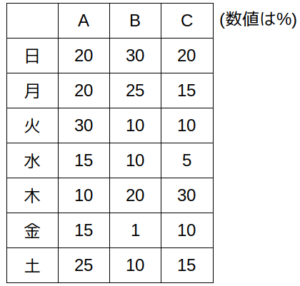
同一の工場で製造される、十分量の食塩水A、B、Cがある。A、B、Cの濃度は、製造された日付の曜日によって決められており、製造された日付の曜日とA、B、Cそれぞれの濃度との対応関係は表の通りである。
ある店では、AまたはBまたはCから一定量の食塩水を取り出して混ぜ、新たにX、Y、Zという3種類の食塩水を作って販売している。Aから300g、Bから100gを取り出して混ぜたものがX、Aから100g、Bから300gを取り出して混ぜたものがY、Cから400gを取り出したものがZである。X、Y、Zを作るために用いたA、B、Cの製造日は全て異なるが、2種類以上の食塩水を取り出して混ぜる場合は、必ず同じ日に製造された食塩水を用いたこととする。例えば、Xに用いたAとBの製造日はともに8月12日、Yに用いたAとBの製造日はともに8月13日で、Zに用いたCの製造日は8月15日であったとする。
ある日、作ったX、Y、Zに含まれる食塩の総量を調べたところ、88gであった。別の日に、同じA、B、Cを用いてX、Y、Zを作ったが、このときのA、B、Cの容器の表記が全て間違っていたことが後に判明した。この間違った表記をもとに作ったX、Y、Zに含まれる食塩の総量を調べたところ、全部で181gであった。このときのYに含まれる食塩は何gか。
- 31g
- 45g
- 55g
- 64g
- 72g
1
食塩水の配合の問題です。
問題文の文量が多いですが、丁寧に読み解きましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
食塩水の問題では、食塩の量の変化に注目するのが定石です。
本問では、X、Y、Zに含まれる食塩の総量が88g→181gと変化したことが述べられており、これが問題を解くカギとなります。
食塩の量を知るのに必要な要素は2つ、「濃度」と「食塩水の量」です。
X、Y、Zについて、後者は問題文の中盤に述べられています。
問題は前者、つまり「濃度」です。
濃度については、「製造された日付の曜日によって決められて」いるとあり、一覧表が与えられていますが、X、Y、Zを作るのに使ったA、B、Cが何曜日に製造されたのかが不明です。
これを解き明かすのに必要な情報が、「ある日、〜、88gであった」という部分です。
X+Y+Z=1200gより、88÷1200≒0.073→7.3%
表に出てくる数値と比べると、これはかなり低めですね。
そこで、試しにX+Y+Zの濃度が最小となるような曜日の組み合わせを考えてみます。
Xについて、「Aから300g、Bから100gを取り出して混ぜたもの」なので、濃度を最小とするにはAの濃度を低くする必要があります。
表を見ると、Aの濃度が最小なのは木曜日なので、Xに用いたAとBは木曜日に製造されたものと仮定します。
Yについては、「Aから100g、Bから300gを取り出して混ぜたもの」なので、Bの濃度が最小となる曜日、つまり金曜日に製造されたものを用いたと仮定します。
Zは「Cから400gを取り出したもの」なので、Cの濃度が最小の、水曜日に製造されたものを用いたと仮定します。
以上、「X:木、Y:金、Z:水」という組み合わせで作った場合の食塩の総量を求めると、
(0.3×300+0.1×100)+(0.15×100+0.01×300)+(0.05×400)
=50+18+20
=88[g]
これで、曜日の組み合わせは正しかったのだと分かります。
ここからは、「別の日に、〜、全部で195gであった」の部分を使って、解答を求めます。
ここでも、考えるべきは「濃度」です。
181gは「間違った表記をもとに」作ったときの総量なので、この「間違った表記」を推測してあげる必要があります。
XYZの曜日は分かったので、どれをどれと取り違えたのかが分かれば、一覧表から濃度を知ることができます。
「A、B、Cの容器の表記が全て間違っていた」とあります。
実は、表記が3つとも間違えている場合の取り違え方は次の2パターンしかありません。
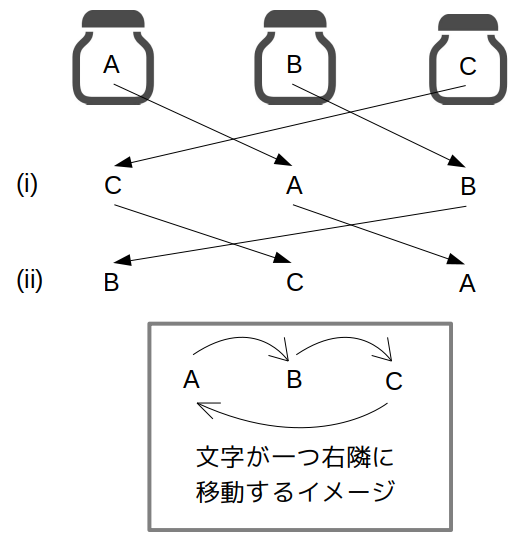
(i)(A、B、C)→(C、A、B)のとき
XYZの配合で、A→C、B→A、C→Bとそれぞれ読み替えましょう。
「X:木、Y:金、Z:水」という曜日の対応にも注意すると、食塩の総量は
(0.3×300+0.1×100)+(0.1×100+0.15×300)+(0.1×400)
=100+55+40
=195[g]
となり、181gとはならず不適です。
(ii)(A、B、C)→(B、C、A)のとき
(0.2×300+0.3×100)+(0.01×100+0.1×300)+(0.15×400)
=90+31+60
=181[g]
これより、(ii)のケースが正しいと分かります。
この場合のYに含まれる食塩は、上の計算より31gです。
よって、1が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
食塩水の配合をテーマとした問題でした。
問題文がかなり長いので、一読しただけで相当疲れてしまった方もいるかもしれません。
最初に必要な情報をハッキリさせて臨みましょう。
特に国家総合職では、この手の読解力が試されるような問題が時たま出現します。
とはいえ、見かけは複雑でも解き方のポイントとなる考え方は単純のそれと何ら変わらない、というケースは多いです。
本問でいえば、溶けている食塩の量に注目する、という基本的な考え方が通用します。
問題演習では、こうした「今までの勉強でも対応できる要素」はないか、探してみてください。
「今ある知識で対応できる」と分かれば、たとえ解けなかったとしても少しは自信がもてるでしょう。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
「ある日、〜、88gであった」という部分について、
X+Y+Z=1200gより、88÷1200≒0.073→7.3%
これは、表に出てくる数値と比べ、かなり低めであることが分かる。
そこで、X+Y+Zの濃度が最小となるような曜日の組み合わせを考える。
同様に、YはBの濃度が最小となる曜日(=金曜日)、ZはCの濃度が最小となる曜日(=水曜日)を仮定する。
以上、「X:木、Y:金、Z:水」という仮定のもとで食塩の総量を求めると、
(0.3×300+0.1×100)+(0.15×100+0.01×300)+(0.05×400)
=50+18+20
=88[g]
これより、「X:木、Y:金、Z:水」という曜日の仮定は正しかったことになる。
次に、「別の日に、〜、全部で195gであった」の部分について、「A、B、Cの容器の表記が全て間違っていた」という条件を満たすのは次の2パターンしかない。
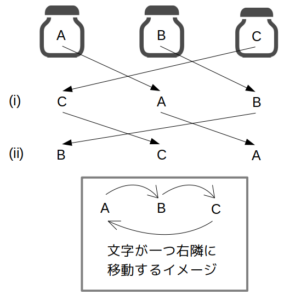
取り違えのパターンは2通り
(i)(A、B、C)→(C、A、B)のとき
XYZの配合において、A→C、B→A、C→Bとそれぞれ読み替え、「X:木、Y:金、Z:水」という曜日の対応に注意すると、食塩の総量は
(0.3×300+0.1×100)+(0.1×100+0.15×300)+(0.1×400)
=100+55+40
=195[g]→不適
(ii)(A、B、C)→(B、C、A)のとき
(0.2×300+0.3×100)+(0.01×100+0.1×300)+(0.15×400)
=90+31+60
=181[g]
このとき、Yに含まれる食塩の量は31gである。
したがって、1が正解である。

コメント
端数が1であるのが金曜日のBだけで、他は5の整数倍であることに注目すべきですね
それだけでも金曜日の塩水がYに使われたと判ります
ラベルが間違えていると端数が1になるので、金曜日のAとしてBが使われてしまったことも判ります
ABが入れ替わってしまった可能性は問題文より存在しないので、他の食塩水の間違いも自動的に判明します
すなわちBの容器にAと書いてあったのならばAの容器にはC、Cの容器にはBと書いてあったのです
結局水木金の塩水を使ったことは突き止めるのですが、それを考慮する前に入れ替えについては見当がつくわけですね
コメントありがとうございます。
ご自分で抜け道を見つけられましたね、さすがです!
筆者も想定外のプロセスで驚きました。
問題演習のとき、「もっと楽な方法はないかな?」と考えてみるのはとてもいいことです。
数的処理は時間との戦いなので、どんどん出題者泣かせの楽な解き方を編み出していきましょう。
よければ他の問題にもチャレンジしていってください。
解説よりもいい解き方が見つかったら、コメントでシェアしてもらえると嬉しいです!