こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、条件をもとに10個の点の位置関係を図に起こす問題でした。
判断推理でありながら、平面図形のセンスが求められる問題です。
ぜひ解いてみてください。
もう解いた方は、お疲れ様でした。
学んだ解法を記憶として定着させるには、繰り返しが肝心です。
一度解いただけではすぐに忘れてしまいますし、繰り返し解くことにより得られる発見もあります。
問題を見て、解法のプロセスを瞬時に頭の中で再現できるまでやり込むといいでしょう。
本サイトで勉強するなら、絶対に「解法のポイント」だけは暗記してください。
個々の解法を、他の問題に応用するためのエッセンスが凝縮されています。
どんなに面倒でも、「解法のポイント」だけは見返しましょう。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
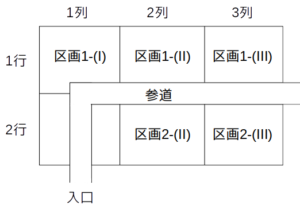
ある神社の境内に、5つの団体A〜Eが露店を出すことになった。図は、出店が可能な区画の見取図で、A〜Eにはそれぞれ異なる位置が割り当てられる。当日は正午に配置換えが行われ、全ての露店が区画を移動することになっている。
この境内では、入口に最も近い1列目の区画から2列目、3列目の順に売上げが高く、同じ列の区画であれば、時間帯によらず売上げは等しくなる。また、露店ごとにみると、区画が1列目だった場合の売上げと2列目だった場合の売上げの比は、区画が2列目だったときの売上げと3列目だったときの売上げの比と等しい。
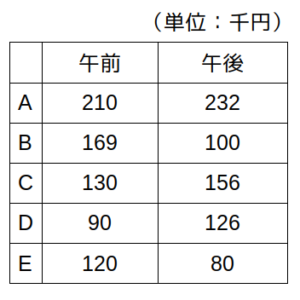
配置換えの前後における各店舗の売上げは表の通りで、区画の割り当てについて、次のことが分かっている。
- 午前中、Bには区画1−(I)が、Dには区画1−(III)が、それぞれ割り当てられていた。
- CとDは、午前午後とも参道をはさんで向かい合う区画が割り当てられていた。
この条件の下、A〜Eの露店における売上げの合計額が最大となるように区画を割り当てたとき、区画1−(I)にある露店の売上げはいくらか。
- 140千円
- 156千円
- 165千円
- 172千円
- 180千円
5
露店の配置と売上げの問題です。
位置関係に言及した条件があることから、区画の割り当てを考える必要があるのだと分かります。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
条件はいずれも露店の位置関係に関するものです。
これは、「午前午後の露店(A〜E)の配置を推理してください」という出題者からのメッセージです。
まずは午前午後の区画の割り当てを明らかにすることを目標としましょう。
まっさらな区画の図を、午前の分と午後の分で2つ用意してください。
最初に、
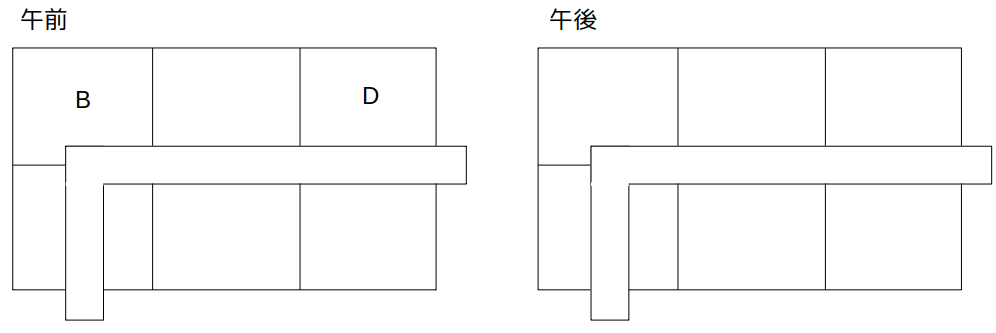
1つ目の条件午前中、Bには区画1−(I)が、Dには区画1−(III)が、それぞれ割り当てられていた。
を図にします。
読んで時の如くです。
ここに
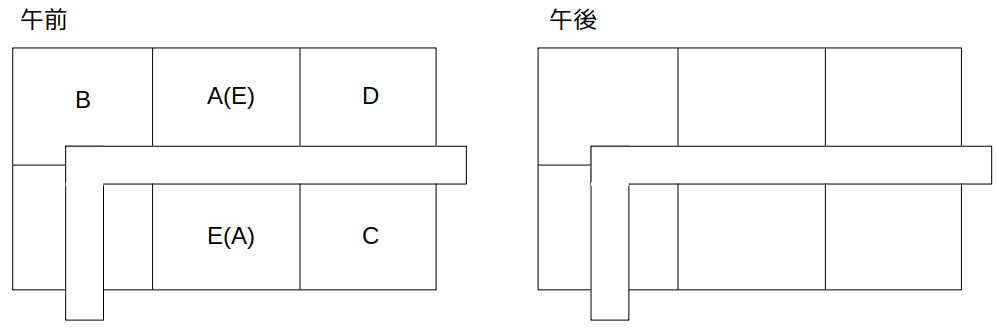
2つ目の条件CとDは、午前午後とも参道をはさんで向かい合う区画が割り当てられていた。
が加わると、午前のCの位置が確定します。
残るAとEは2列目で、「AE」なのか「EA」なのか確定しませんが、「同じ列の区画であれば、時間帯によらず売上げは等しくなる」ので、どちらでもOKです。
続いて午後の配置ですが、ここは表の数字から決まります。
問題文の「入口に最も近い1列目の区画から2列目、3列目の順に売上げが高く、同じ列の区画であれば、時間帯によらず売上げは等しくなる」という箇所に注目です。
表によると、AとCとDは午前→午後で売上げがアップしています。
このことから、これらは配置換えによって、より入口に近い区画に移動したのだと分かります。
すると、午後のAは区画1−(I)に決まります。
これにより、CとDは配置換えで2列目に移動したことが分かります。
残るBとEは3列目になります。
CとD、およびBとEはともに順不同です。
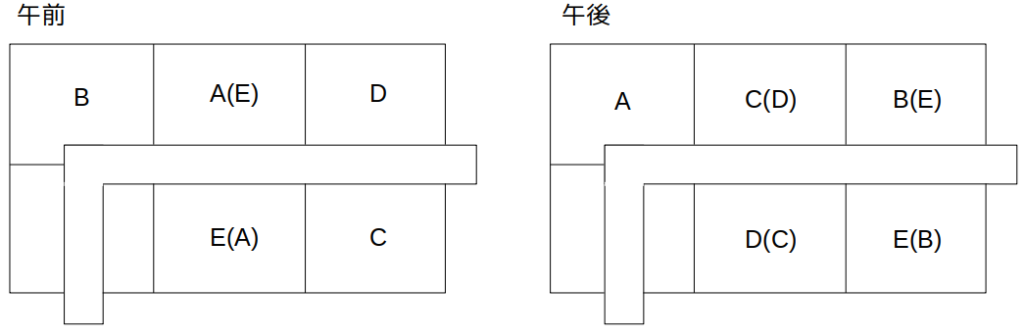
これで、午前午後の配置が決まりました。
次に注目すべきは、問題文の「また、露店ごとにみると、区画が1列目だった場合の売上げと2列目だった場合の売上げの比は、区画が2列目だったときの売上げと3列目だったときの売上げの比と等しい。」という箇所です。
最終的には売上げが最大となる配置を考えなければならないので、列の移動に伴う増減の倍率(=列の移動により、どれくらい売上げがアップ/ダウンするのか?)を知る必要があります。
区画の図と表を見比べながら、これを明らかにしていきましょう!
まずAについて。
Aは配置換えにより列一つ分だけ入口に近づいています。
この結果、売上げが210→232と変化しています。
比にして1.1倍の増加です。
これより、Aは列一つ分の移動ごとに売上げが1.1倍されることが分かります。
(ここで言う「移動」は、入口に近づく変化のことを指します)
次にBですが、Bは配置換えにより列二つ分だけ入口から遠ざかっています。
これにより、売上げは169→100と変化しています。
Aに合わせて増加の倍率を考えるには、午後を基点にすればOKです。
つまり、Bは列二つ分の移動で売上げが1.69倍される、といえます。
1.69は1.3の2乗なので、列一つ分の移動では1.3倍、となります。
同じようにC、D、Eの増加率を求めると、列一つ分の移動あたり、それぞれ1.2倍、1.4倍、1.5倍です。
増加率が分かったところで、売上げを最大化する配置を考えましょう。
といっても、問題の主旨はあくまで「区画1−(I)」に置かれる店の売上げを求めることなので、この区画にはA〜Eのうちのいずれを置くべきかにだけ注目すれば十分です。
(5つ全ての配置を明らかにする必要はありません)
2列目→1列目という配置換えがあった場合の増加額をA〜Eそれぞれで求めます。
最も増加額が多い団体こそ、区画1−(I)に置くべき店です。
まずAについては、表の数字から求められます。
2列目にあるときの売上げが210なのに対し、1列目のときは232で、増加額は232−210=22(千円)
Bについては、2列目にあった場合の売上額を自力で算出する必要があります。
Bが3列目→2列目と移動すると売上げが1.3倍になるので、午後の売上げより100×1.3=130(千円)
これと午前の売上げより、増加額は169-130=39(千円)
Cは2列目にあった場合(=午後)の売上げが分かっているので、ここから増加額が求められます。
増加率が1.2倍なので、156×0.2=31.2(千円)
DとEも同様にして増加額を求められます。
D:126×0.4=50.4(千円)
E:120×0.5=60(千円)→最大
以上より、売上げを最大化するように露店を配置したとき、区画1−(I)にはEがあります。
このときの売上額は、120+60=180(千円)
よって、5が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
前半は位置関係、後半は比をテーマにした複合的な問題でした。
まずは箇条書きされた条件をもとに、午前の配置を確定しましょう。
配置換えの結果である午後の配置は、売上額の上下から判断します。
後半は列の移動に伴う売上額の増加率を求めたら、区画1-(I)に移動した場合に売上げがどの程度アップするかを数値で比較します。
箇条書きの条件が位置関係に関するものであることから、区画の割り当てを明らかにするプロセスは必須であると分かります。
問題文をよく読むと、解答の方針が見つかることがあります。
問題文が与えるヒントを見逃さないように、日頃から注意するクセを身に付けたいところですね。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
1つ目の条件「午前中、Bには区画1−(I)が、Dには区画1−(III)が、それぞれ割り当てられていた。」
より、BとDの午前の配置は次のようになる。
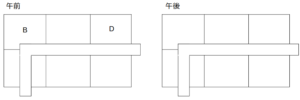
午前のBとDの位置
残るAとEは2列目で、順不同である。
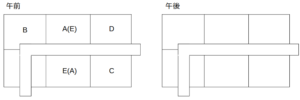
午前の割り当てが確定
午後の配置については、問題文の「入口に最も近い1列目の区画から2列目、3列目の順に売上げが高く、同じ列の区画であれば、時間帯によらず売上げは等しくなる」という箇所から決まる。
表によると、AとCとDは午前→午後で売上げがアップしているから、これらは配置換えによって、より入口に近い区画に移動したことになる。
これより、午後のAは区画1−(I)に決まる。
また、CとDは配置換えで2列目に移動したことになる。
残るBとEは3列目に決まる。
CとD、およびBとEはいずれも順不同である。
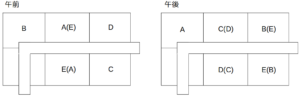
午後の配置が決定
次に、問題文の「また、露店ごとにみると、区画が1列目だった場合の売上げと2列目だった場合の売上げの比は、区画が2列目だったときの売上げと3列目だったときの売上げの比と等しい。」という箇所に注目する。
売上げが最大となる配置を考えるため、列の移動に伴う増減の倍率(=列の移動により、どれくらい売上げがアップ/ダウンするのか?)を明らかにする。
まずAについて、Aは配置換えにより列一つ分だけ入口に近づき、売上げが210→232と変化している。(1.1倍)
次にBについて、Bは配置換えにより列二つ分だけ入口から遠ざかり、売上げは169→100と変化している。
午後を基点に考えると、Bは3列目→1列目の移動で売上額が1.69倍となる。
1.69は1.3の2乗だから、列一つ分の移動では1.3倍、となる。
同様にC、D、Eの増加率を求めると、列一つ分の移動あたり、それぞれ1.2倍、1.4倍、1.5倍である。
以下、2列目→1列目という配置換えがあった場合の増加額をA〜Eそれぞれで求め、区画1-(I)に露店を置くべき団体を特定する。
まずAについて、表より、増加額は232−210=22(千円)
Bについて、まず2列目にあった場合の売上額は、午後の売上げより100×1.3=130(千円)
これと午前の売上げより、増加額は169-130=39(千円)
Cは2列目にあった場合(=午後)の売上げが、1列目に移動すると1.2倍されるので、増加額は156×0.2=31.2(千円)
DとEも同様にして増加額を求める。
D:126×0.4=50.4(千円)
E:120×0.5=60(千円)→最大
以上より、売上げを最大化するように露店を配置したとき、区画1−(I)にはEがある。
このときの売上額は、120+60=180(千円)
したがって、5が正解である。

コメント