こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、システムが出力する値から入力値を推測する問題でした。
条件をうまく読み取って活用する思考力と正確な計算力が要求される問題です。
ぜひ解いてみてください。
- 判断推理の位置関係で、最初に注目すべきポイントが分かる
- 過去問の類題を例に、本番で役立つ「解法のポイント」の使い方を学べる
- どこよりも詳しい演習問題の解説で、本試験レベルの問題を完全理解
→数的処理の「あと一点」が実現!
数的処理の判断推理は、何といっても「文章題」がメインです。
文章題は判断推理の中核をなす分野なだけあって、毎年“必ず”出題されています。

むしろ文章題が1問もない数的処理とかコワすぎる
にもかかわらず、数的処理の文章題に苦手意識をもつ人は多いです。
確率とか図形みたいな分野は受験でみっちり詰め込むのに、文章題なんて学校教育の科目にないですから、戸惑うのも無理はないと思います。

生涯公立校一本だった筆者も苦労したっけ
その文章題の一角を占めるのが「位置関係」です。
数的処理では、対応関係に次いで頻出の重要分野。
公務員試験では差が付きやすいトコロだったりします。
そんな位置関係を解くための「コツ」があるとしたら、知りたくありませんか?
この記事では、数的処理の位置関係を解くためのコツである「解法のポイント」を紹介します。
それから過去問の類題を一緒に解いて理解してもらうことで、本番で使える解法を身につけていってもらいます!
講義:数的処理の位置関係を解くコツ
数的処理の位置関係は、文量の多い条件から処理するのがコツです。
文量の多い条件に注目
文章題は制約がキツイ条件からやっつけるのが定石です。
制約がキツイ方が、その後の分岐の可能性を減らせるので、場合分けが少なくて済みます。
条件文が長いのは、それだけ制約が厳しいということですから、位置関係は文量の多い条件から処理していくのがセオリーです。

いかにも簡単そうな短い条件文から手を付けたくなるのをグッとこらえて
(問)
(答)
【位置】問題1 | 公務員試験数的処理解法テクニック KOMARO
上の例題では、最も文量の多い条件「ア」を最初に処理しています。
解説の通り、次の条件「エ」ではBの位置(1マス分)しか分かっていないのに対し、「ア」ではAとC+空きロッカーの計3マスが一挙に確定しています。
AとCと空きロッカーの3マスの位置取りが先に決まれば、その後の検討が少なくて済みます。

カギカッコの形が収まる場所は限られるから、分岐の見通しが良くなる
演習問題:同じ平面上にある10個の点の位置関係
同一平面上に分布する10点A〜Jが次の条件を満たすとき、点の位置関係について確実に正しいといえる選択肢はどれか。
- AB=AE=AF
- 6点A、C、E、F、G、Iは、点Bを中心とする一つの円上にある。
- CB=CG=CI
- GA=GI、かつGC=GE
- 4点A、B、J、Cはこの順に同一直線上にあり、かつAJ=3BJ
- △DHJは正三角形で、かつ3点D、H、Jは点Bを中心とする一つの円上にある。
- CJ=DF
- DH=GJ
- DI=FG
- DJ=GH
- FH=CJ
2
点の位置関係の問題です。
条件をもとに図を描いてみましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
本問は点の位置関係の話なので、条件を図(マップ)に起こすのが有効だと考えられます。
そして、どの条件から手を付けるかも重要です。
位置関係は文量の多い条件から手を付けるのが定石です。
文量の多い条件に注目
Bを中心とする同一の円上に6点ACEFGIが並ぶ
本問では、まず
2つ目の条件6点A、C、E、F、G、Iは、点Bを中心とする一つの円上にある。
に注目して図を描いてみるのがいいでしょう。

7つもの点の位置関係を一挙に把握できるのはオイシイ
6点の配置について、 5つ目の条件4点A、B、J、Cはこの順に同一直線上にあり、かつAJ=3BJ の前半の内容を踏まえて、2点A、Cは点Bをはさんで対向するように配置します。
6点ACEFGIの位置関係を確定させる
また、
1つ目の条件AB=AE=AF
より、△ABEと△ABFはともに正三角形です。
同様に、
3つ目の条件CB=CG=CI
より、△BCGと△BCIも正三角形です。
ここまでを図にすると、次のようになります。
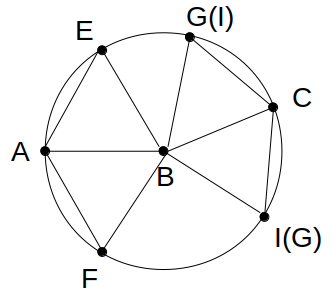

(お、正六角形か?)
ここに5つ目の条件の「4点A、B、J、Cはこの順に同一直線上」を加味すると、6点は点Bを中心とする円上に等間隔で並ぶことになります。
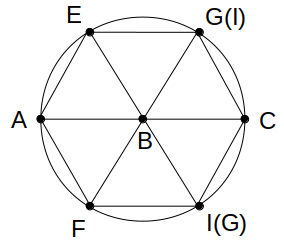
ここまでだと2点G、Iが順不同ですが、 4つ目の条件GA=GI、かつGC=GE の後半「GC=GE」より、点Gは点Eの隣に決まります。
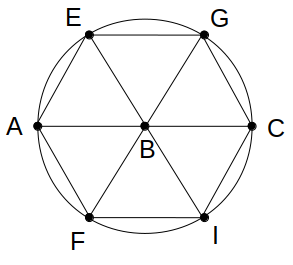
残りの条件を使って3点DHJの位置関係を考える
あと使っていない条件は、5つ目の条件の「AJ=3BJ」と、
6つ目の条件△DHJは正三角形で、かつ3点D、H、Jは点Bを中心とする一つの円上にある。
の2つだけです。
ここからは、この2つについて考えていきましょう。
まず「AJ=3BJ」を図に書き加えます。
「4点A、B、J、Cはこの順に同一直線上」に注意すると、点Jの位置は線分BCのちょうど真ん中、中点になります。
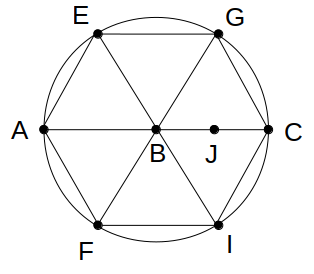
あとは6つ目の条件「△DHJは正三角形で、かつ3点D、H、Jは点Bを中心とする一つの円上にある。」ですね。
点Bを中心に点Jを通る円を描くと、2点D、Hはこの円上のどこかに存在します。
△DHJは正三角形である、ということは、3点D、H、Jはこの円を三等分する点であるはずです。
つまり、線分BEおよび線分BFの中点が2点D、Hです。(ただし、順不同)
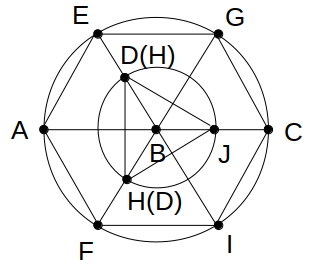
この図をもとに選択肢を検討すると、確実に正しいといえるのは2だけです。
よって、2が正解です。
おわりに:位置関係は長い条件文に注目
お疲れ様でした!
いかがだったでしょうか?
位置関係は文量の多い条件から手を付けると見通しが良くなります。
図を描いて可視化しながら進めるのも大切。
10個あるポイントの位置関係を明らかにする問題でした。
条件をもとに、図(マップ)を描くのが目標となります。
カテゴリ的には判断推理の「位置関係」の問題なので、「制約条件の厳しい条件から」というコツが使えます。
2つ目の条件は一挙に6点+1点の位置関係を扱えるので、ここから手を付けると見通しが良くなります。
純粋な図形の問題とは異なり、ゼロベースで自ら図を描かなければならないところが本問の特徴であり、難しさだと言えるでしょう。
本番なら、多少の試行錯誤は覚悟の上、残り時間を考慮して解くかどうかの判断をすることになります。
ぱっと見で自信がなければ、潔く捨てるのも一考だな、という考えは常に持っておきましょう。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
まず、2つ目の条件「6点A、C、E、F、G、Iは、点Bを中心とする一つの円上にある。」を図に起こす。
また、1つ目の条件「AB=AE=AF」より、△ABEと△ABFはともに正三角形である。
同様に、3つ目の条件「CB=CG=CI」より、△BCGと△BCIも正三角形である。
ここまでを図にすると、次のようになる。

同一の円上&正三角形
ここに5つ目の条件の「4点A、B、J、Cはこの順に同一直線上」を加味すると、図形AEGCIFは正六角形に決まる。

6点ACEFGIの並び
ここに「AJ=3BJ」を書き加える。
「4点A、B、J、Cはこの順に同一直線上」に注意すると、点Jの位置は線分BCの中点となる。
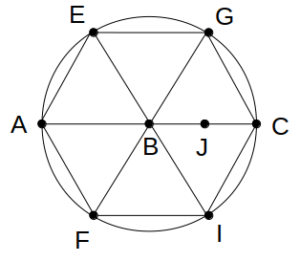
点JはBCの中点
6つ目の条件「△DHJは正三角形で、かつ3点D、H、Jは点Bを中心とする一つの円上にある。」について、△DHJは正三角形である、より、3点D、H、Jは点Bを中心とする小円を三等分する点となる。
線分BEおよび線分BFの中点が2点D、Hである。(ただし、順不同)
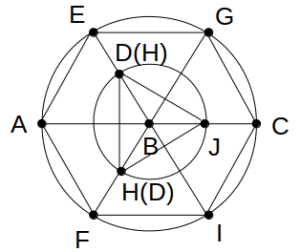
2点D、Hの位置が確定
この図をもとに選択肢を検討すると、確実に正しいといえるのは2しかない。
したがって、2が正解である。



コメント
D,Hが順不同なのはわかりますが、E,FとG,Iはどの条件から順序が定まるのでしょうか?
コメントありがとうございます。
私のミスで、4つ目の条件「GA=GI、かつGC=GE」に対する考察が抜けておりました。
この条件より、GはEの隣に決まります。
EとFの位置は、ACに関する対称性より、解説のように最初から決め打ちして考えることができます。
もし納得できなければ、EとFが逆になったバージョンを描いてみて選択肢を検討するのもアリです。
(本番だったらそこまで深追いせずに解答を選んでも大丈夫かと思います)
ご不明な点などあれば、またコメントください!