こんにちは！
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【２】どこよりも詳しい解説
【３】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験を受ける方は必見！
ぜひ最後まで読んでいってください。
「解法のポイント」はないこともある、かもしれない
今回のテーマは……「うそつき問題」
中学受験した人は得意かも。
数的処理で出題されたらチャンス。
なぜって、うそつき問題は解き方が決まっているからです。
うそつき問題を解くキーワードは、【仮定と検証】
具体的には、うそつきを仮定して矛盾が生じるか調べるのがキホンの解き方となります。
今回は、試験に出るレベルの問題を解きながら、うそつき問題の解き方を学んでいきます。
使うのはもちろん、数的処理の過去問を模した演習問題。
演習問題：宇宙人の村でうそつきを探す
ある村に、一般人に紛れて宇宙人が何人か住んでいる。宇宙人を見つけ出すため、この村の住人であるA～Eに、互いが宇宙人かどうかについて情報を求めたところ、次のように回答した。
A「CとDのうち、一方のみ宇宙人である。」
B「Aが宇宙人なら、Cも宇宙人である。」
C「Dは宇宙人である。」
D「AとBはいずれも宇宙人である。」
E「Dが宇宙人なら、Eは一般人である。」
宇宙人および一般人について、一方は常に正しい発言をし、他方は常に誤った発言をすることが分かっている。このとき、確実に正しいのは次のうちどれか。
- Cは宇宙人である。
- A～Eのうち、一般人は全部で4人いる。
- Dは宇宙人である。
- Eは一般人である。
- A～Eの中に、確実に宇宙人であるといえる者はいない。
５
うそつきを仮定する、その前に。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者
おそすぎる自己紹介
それでは、解説スタート！
解説：宇宙人はうそつき、とは限らない
A～Eの発言と、後半の一文“一方は常に正しい発言をし、他方は常に誤った発言をする”という設定は、「うそつき問題」そのもの。
うそつき問題には、【仮定と検証】
うそつきを仮定して矛盾を探します。
誰かをうそつきと仮定して矛盾が見つかれば、仮定が間違っていたということになります。
つまり、その人はシロ（発言は正しい）。
本問も、A～Eのだれかをうそつきと仮定してみて、矛盾があるか調べます。
が！
ここで一つ問題が。
宇宙人はウソつきなの？正直者なの？
「バカなの？死ぬの？」的に
ふつう、うそつき問題ではどんな人がウソをつくか、が決められているもの。
例）犯人、悪魔
ところが、本問は宇宙人と一般人、どちらがうそつきなのかが不明です。
決められていない以上は、こちらで決め打ちして進めるしかありません。
つまり場合分け。
以下、宇宙人が(i)正直者の場合と、(ii)うそつきの場合を考えていきます。
一般人（以下パンピー）はその逆ね
(i)宇宙人が正直者（一般人はうそつき）の場合
まずは宇宙人＝正直者（パンピー＝うそつき）の世界。
宇宙人ウソツカナイ
ホントぉ？
※「インドジン・ウソツカナイ」って品種の唐辛子が実在するそうです
トウガラシ【インドジン・ウソツカナイ】インド人も納得の辛さ｜トキタ種苗生のまま箸休め的にかじって食べる。カレーの味付けにインドで一番多く使われている種類の品種。インド人も納得の辛さ。ワタ部を除くと辛みはやや和らぐが、果肉もやや辛い.
「解法のポイント」にしたがい、誰かにうそつきのレッテルを貼って矛盾があるか調べます。
試しにAをうそつきとしてみます。
Ａをうそつき（一般人）と仮定
“A「CとDのうち、一方のみ宇宙人である。」”
Aの発言がウソ、といえるのは、次のいずれかのとき。
・CもDも宇宙人（正直者）C＝正直者→Cの発言よりD＝宇宙人＝Cで矛盾しない
・CもDもパンピー（うそつき）C＝うそつき→Ｃの発言よりＤ＝一般人＝Ｃで矛盾しない
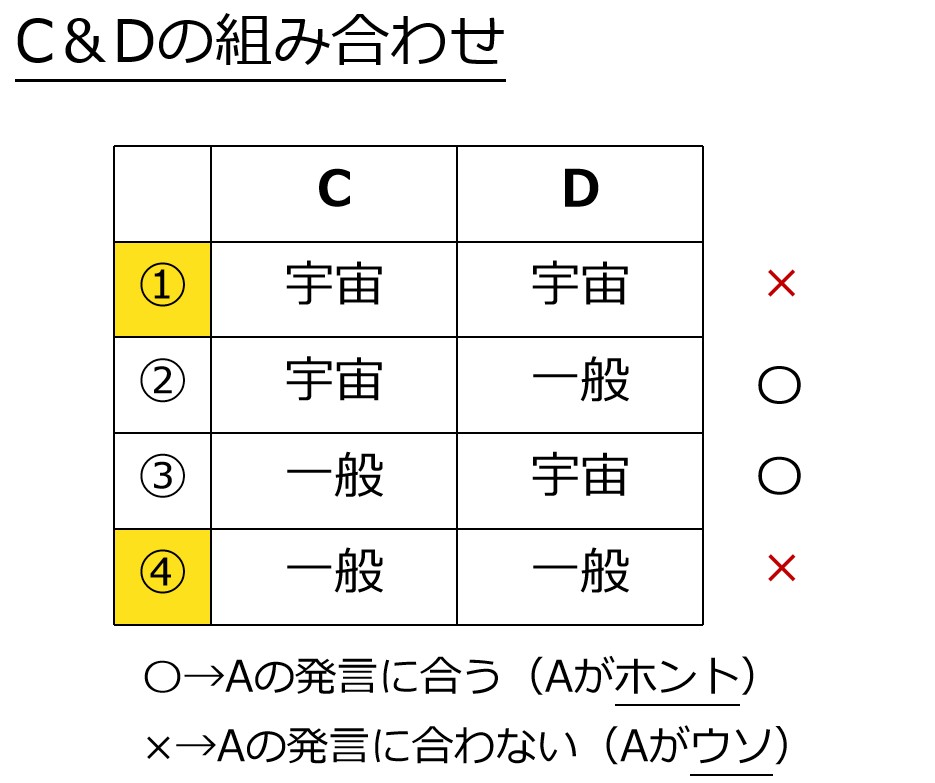
いずれにしろ、C＝Dになる
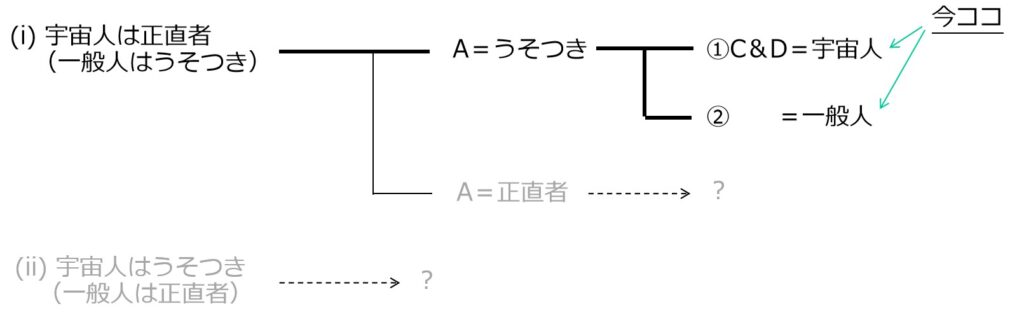
Dの発言はウソ→一般人
“D「AとBはいずれも宇宙人である。」”
今はA＝パンピーなので、Dはうそつき。
→D＝パンピー＝C
BとEは？→ともに不明
“B「Aが宇宙人なら、Cも宇宙人である。」”
繰り返しますが、Aはパンピー。
なので、Bの発言がウソなのかどうか、判断することができません。
→Ｂ＝宇宙人 or 一般人
同じ考え方で、Ｅ＝宇宙人 or 一般人
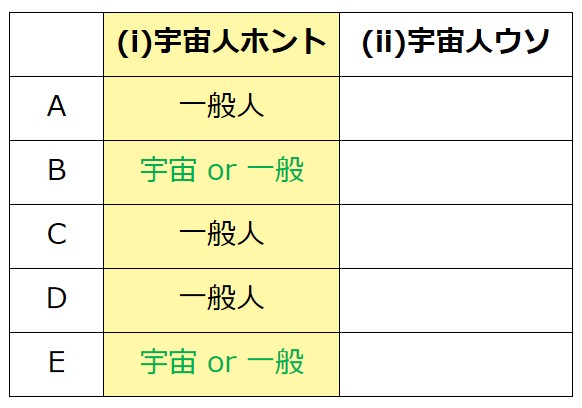
(ii)→×：宇宙人はうそつき（一般人は正直者）の場合
今度は、宇宙人＝うそつき（パンピー＝正直者）の世界。
宇宙人＝バカ ＆ 一般人＝死ぬ、そんな世界（？）
Aをうそつき（＝宇宙人）と仮定→矛盾
Aの発言がウソ、といえるのは、次のいずれかのとき。
・CもDも宇宙人（うそつき）→×Cの発言はウソ→D＝一般人≠宇宙人で矛盾
・CもDもパンピー（正直者）→×Cの発言はホント→Ｄ＝宇宙人≠Ｃで矛盾
この通り、Aをうそつきとすると他の発言に矛盾が生じます。
⇒(ii)は×
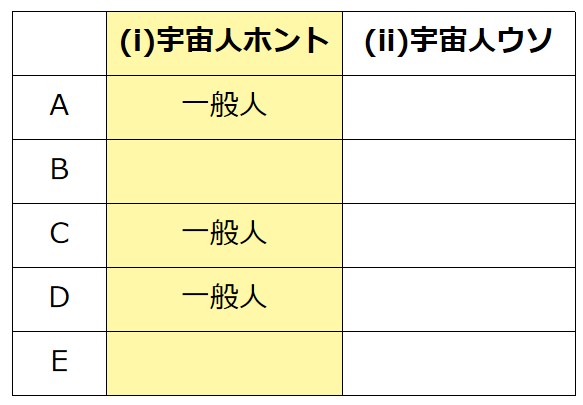
結局、全ての発言を矛盾なく成立させられるのは(i)のパターンだけ。
A～Eが宇宙人かどうかは下表の通り。
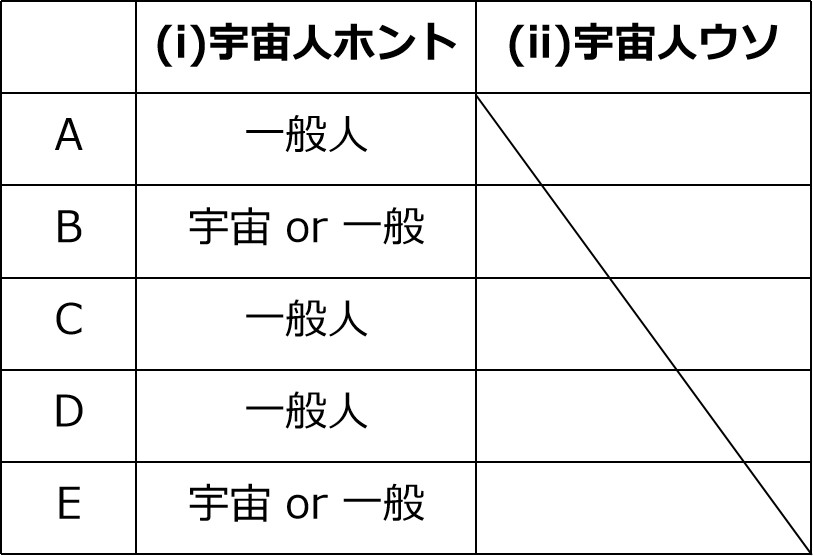
表によると、確実に正しいといえる選択肢は５。
よって、５が正解です。
おわりに：うそつき問題は仮定と検証で解く
お疲れ様でした！
うそつき問題には【仮定と検証】
1人をうそつき認定してみて、矛盾があればその人はシロ。
うそつきが複数人いる場合も同じ。
一人ずつ【仮定と検証】を繰り返し、うそつきをあぶり出します。
本問は、2つのグループのどちらがうそつきか分からない、という問題でした。
宇宙人のウソ/ホントで場合分けの一手間が必要ですが、その先は複数人のうそつき問題。
うそつき認定したら、発言内容をていねいに読み取ります。
まだまだあるぞ！うそつき問題↓
すいか１玉食べ切ったあとの冷蔵庫は、少し寂しい
でもまたすぐ満タンになる
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！
この記事が参考になったら、ぜひシェアしてください！
Tweet次回もお楽しみに！
コメント
私はCを起点に考えたのですが、一般人が正直者でなおかつAとCが一般人でDが宇宙人の場合も考えられると思います。
この場合を含めても正解が5であることに変わりはありませんが。