こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「確率(&場合の数)」
確率で、同じ操作を繰り返す、という設定は定番中の定番。
確率の世界では、繰り返しの操作を「反復試行」といいます。
反復試行の確率を解くためのカギは2つ。
独立と数え上げ
本サイトの「解法のポイント」でいうと、数え上げと確率から確率をどっちも使うパターンです。

旅先でソフトクリーム食べるとき絶対ハーフ選んじゃう
今回は、反復試行の確率の解き方を、数的処理の過去問みたいな演習問題を使って解説します。
演習問題:あたりくじを4本以上引く確率
あたりくじとはずれくじが1本ずつ入った6つの箱がある。いま、いずれかの箱にはずれくじを1本だけ加え、全ての箱から1本ずつくじを引くとき、あたりくじを4本以上引く確率はいくらか。
- \(\frac{11}{24}\)
- \(\frac{3}{8}\)
- \(\frac{13}{24}\)
- \(\frac{5}{8}\)
- \(\frac{7}{24}\)
5
くじを引く、という操作を6回繰り返します。
=反復試行の確率の問題
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:独立の確率はかけ算、排反は足し算
あたりくじが4本以上、というのは、次のいずれかです。
計6本のうち、あたりが
(i)6本
(ii)5本
(iii)4本
(i)~(iii)は同時に起こることはない(=互いに排反)ため、分けて扱う必要があります。
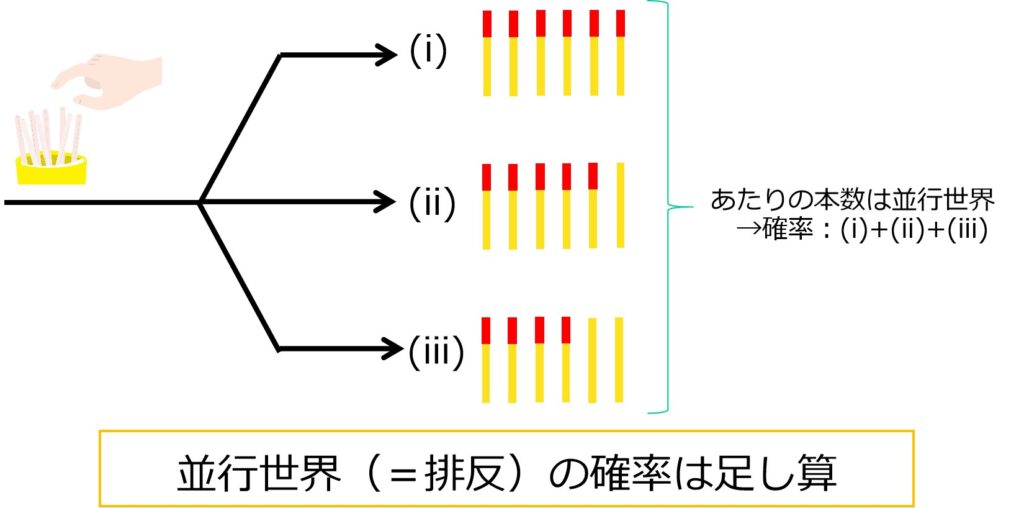
(i)~(iii)の確率を別個に求めて足し合わせる、という方針が浮かびます。

排反は足し算で
また、各回のくじの結果は次の結果に影響しません。
→2箱目があたりだろうがはずれだろうが、3箱目の確率は変わらない(=互いに独立)
つまり、(i)~(iii)の各パターンの確率は、各箱のあたりの確率をかけ算したものになります。

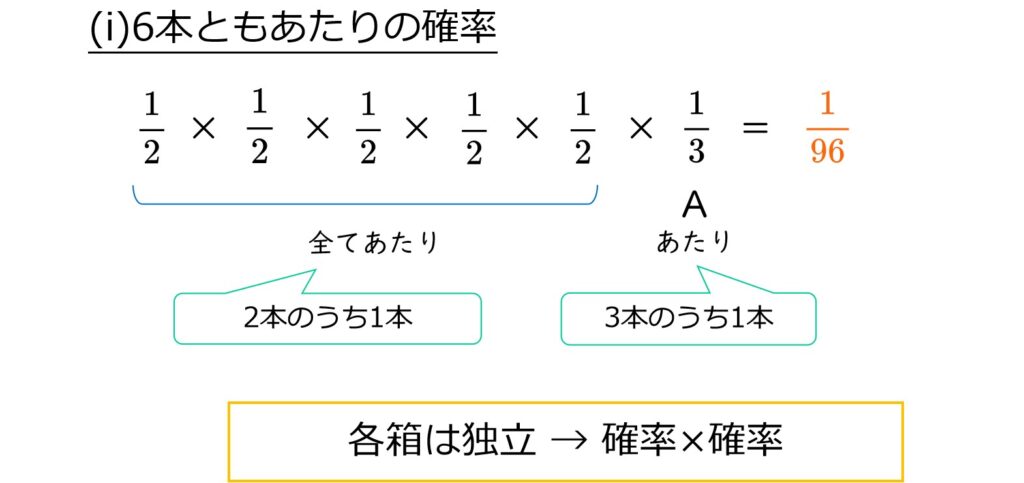
(i)あたり6本:独立のかけ算→確率\(\frac{1}{96}\)
あたりくじとはずれくじが1本ずつなら、あたりの確率は各箱とも\(\frac{1}{2}\)
ただし。
はずれを1本加えた箱(Aとします)だけ、あたりの確率は\(\frac{1}{3}\)
各箱は独立、ということで、確率のかけ算です。
→\(\frac{1}{2}\)を5回、\(\frac{1}{3}\)を1回をかけ合わせます

5倍じゃないよ、5乗だよ
(ii)あたり5本:Aの結果で場合分け→確率\(\frac{7}{96}\)
はずれ1本がAから出るのか否か、で状況が異なります。
Aではずれの確率は\(\frac{2}{3}\)、それ以外はあたり(確率\(\frac{1}{2}\))なので、
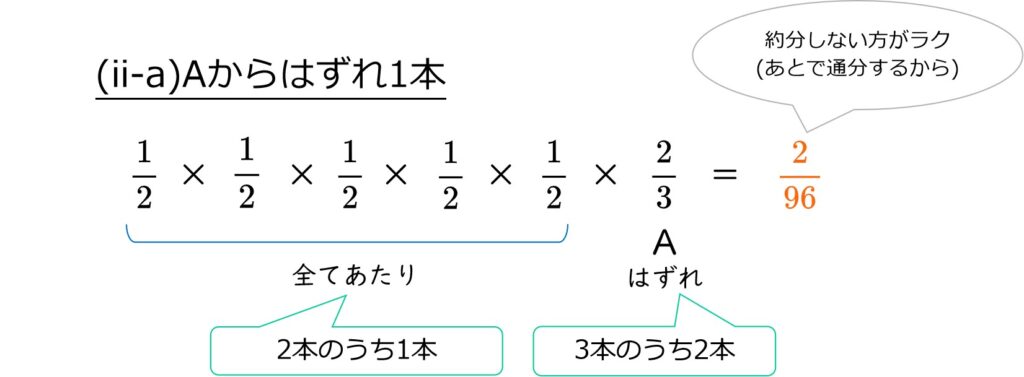
A以外の箱ではずれを引く確率は、いずれの箱も\(\frac{1}{2}\)
そして、A以外の箱を区別すると、「どの箱からはずれを引くか?」も考える必要があります。
⇒はずれのパターンを数え上げてかけ算
5箱をP~Tと区別すると、はずれの箱の選び方は5通りなので、
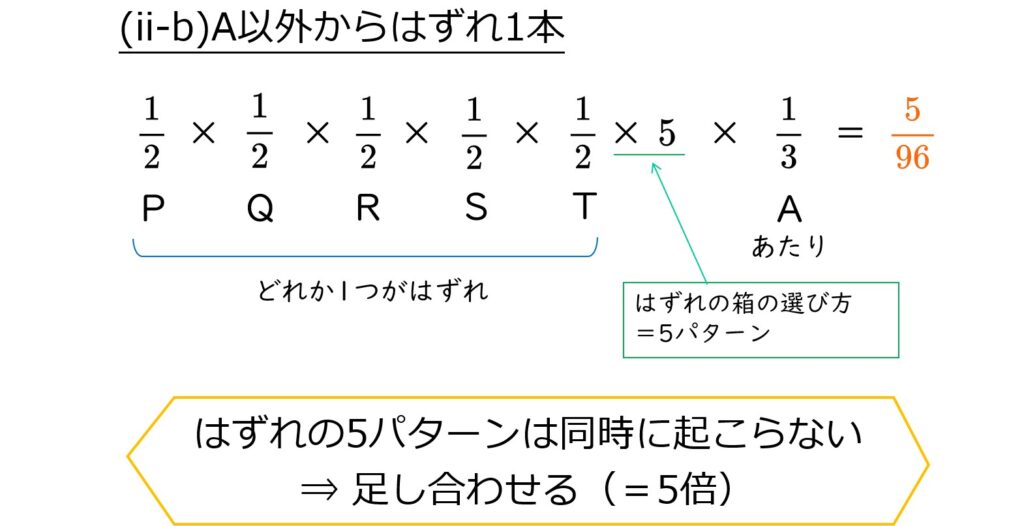
(ii-a)と(ii-b)は同時に起こらない(=排反)ので、あたりを5本引く確率は
\[
\frac{2}{96}+\frac{5}{96}=\frac{7}{96}
\]
(iii)あたり4本:はずれ2本は組み合わせで→確率\(\frac{20}{96}\)
ここも、Aではずれを引くか否か、を分けて考えます。
Aではずれを引く確率は\(\frac{2}{3}\)
A以外は、はずれ1箱&あたり4箱(いずれも確率\(\frac{1}{2}\))となればOK。
はずれの箱の選び方は5通りなので、
\[
\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×5×\frac{2}{3}=\frac{10}{96}
\]
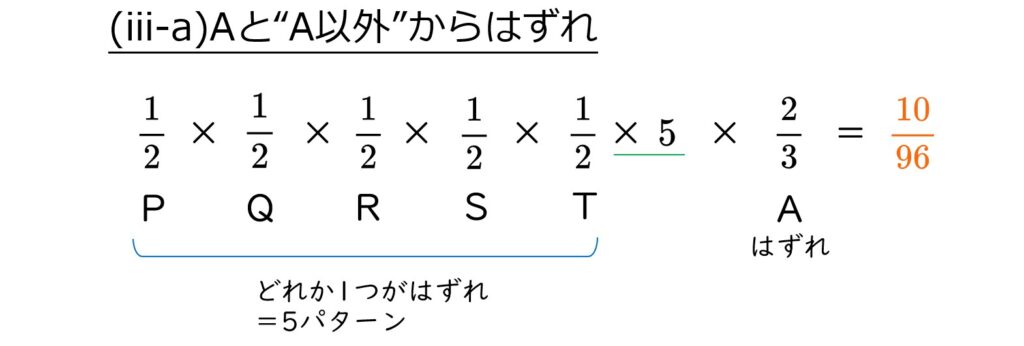
Aであたりを引く確率は\(\frac{1}{3}\)
A以外は、あたり3箱&はずれ2箱(いずれも確率\(\frac{1}{2}\))
箱を区別する場合のはずれの箱の選び方は、5箱から2箱とる組み合わせの数で10通り。
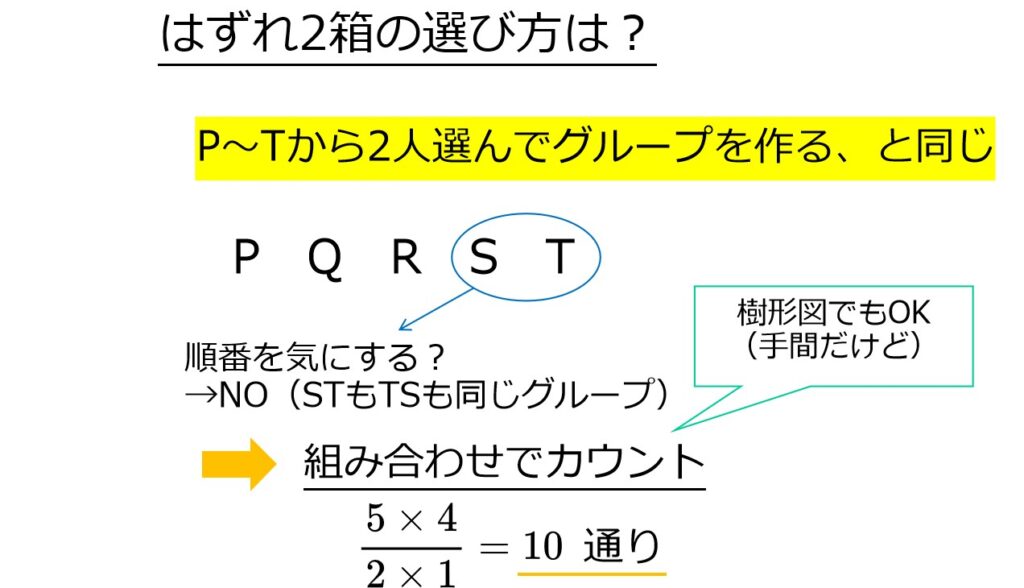
A以外の2箱からはずれを引く確率は、
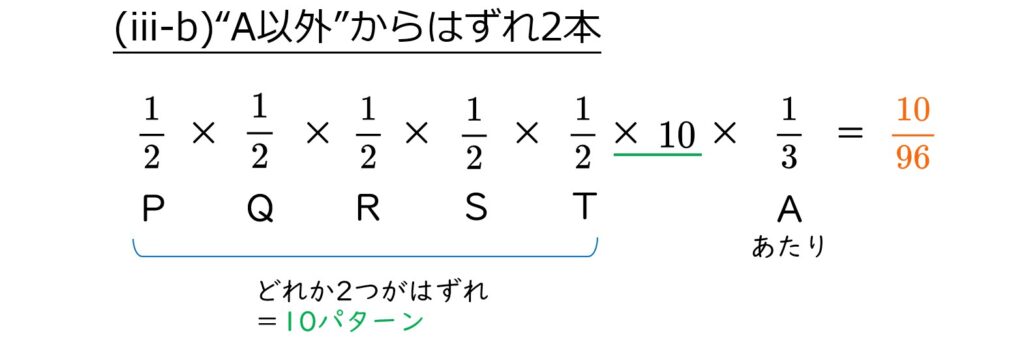
(iii-a)と(iii-b)は同時に起こらないので、あたりを4本引く確率は、
\[
\frac{10}{96}+\frac{10}{96}=\frac{20}{96}
\]
(i)~(iii)も、同時に起こらないので足し合わせます。
あたりを4本以上引く確率は、
\[
\frac{1}{96}+\frac{7}{96}+\frac{20}{96}=\frac{28}{96}=\frac{7}{24}
\]
以上より、5が正解です。
おわりに:反復試行の確率には、独立&数え上げ
お疲れ様でした!
繰り返しの確率を解くカギは、独立と数え上げ
本問の(というか反復試行の)確率をごく単純化すると、次のようになります。
(特定の箱からはずれを引く確率)×(箱の選び方)
あたりの箱が決まっていれば、各箱の確率は独立なので、確率同士のかけ算で求められます。
箱の固定を解くと、箱の選び方の数だけ正解のパターンが増えるので、数え上げてかけ算します。
繰り返しの操作の確率には独立と数え上げ、という回でした。
以下、参考。
確率のパターン(解法のポイント)を学ぼう↓
やさしめ
近所の人懐っこい野良猫に会いたいけどあまり見かけない

タウンマップに表示してくれればいいのに
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!





コメント