こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「整数」
整数ってスゴイんです。
「整数である」という条件があるだけで、たった一つの式から2つ3つの未知数がわかっちゃうことも。

普通は未知数と同じ数だけ式が必要になる
ともかく。
整数問題の解き方には一定のパターンがあるって知ってますか?
整数、という数の性質をテーマとする以上、問題のバリエーションにも限りがあるからです。
整数問題を攻略するコツは、定番の解き方を知ること。
今回は、約数を使うパターンをピックアップ。
大事なのはこれ↓
(A式)×(B式)=整数
この形に表せば、約数のペアを書き出してしらみつぶしできるよね、という考え方です。
今回も、数的処理の過去問みたいな問題を使って、定番の解き方を学びます。

中学数学の知識があればイケる
演習問題:約数を利用した整数問題
次の式を満たす整数\(a,b,c\)について、\(a+b+c\)はいくらか。
ただし、\(0<a<b<c\)とする。
\[
a^2b^4+4a^2b^2+4a^2-c^2-105=0
\]
- 7
- 8
- 11
- 14
- 17
2
実質的に\(a,b,c\)を求めよ、という問題。
与えられた式をじっと眺めてみると……?
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:因数分解で「約数×約数=整数」に持ち込む
\(a+b+c\)を求めよ、という問題。
単純に考えれば、\(a,b,c\)がいくつなのかが分かればOKです。
しかも、条件に注目。
“整数\(a,b,c\)について、~。ただし、\(0<a<b<c\)とする”
これ、もう「\(a,b,c\)を求めて」って言わんばかりでしょ?

はっきり言えばいいのに、素直じゃないんだから
整数の重要な性質の一つが、「約数」
登場人物が全て整数なら、【(A式)×(B式)=整数】の形はすなわち「A式(or B式)=約数」
本問も、次の式を変形して【(A式)×(B式)=整数】の形を作り出します。
みんな大好き「因数分解」を使います。
\[
a^2b^4+4a^2b^2+4a^2-c^2-105=0……(☆)
\]

因数分解が、お好きでしょ♪(?)
以下、【(A式)×(B式)=整数】を念頭に置きながら式変形していきます。
因数分解の定石その1:共通因数でくくる
因数分解は、まず共通因数でくくること。
次数(右肩に乗ってる数)が少ない文字に注目すると、大抵うまくいきます。
式☆であれば、次数が少ないのは\(a\)。
\(a^2\)でくくってみます。
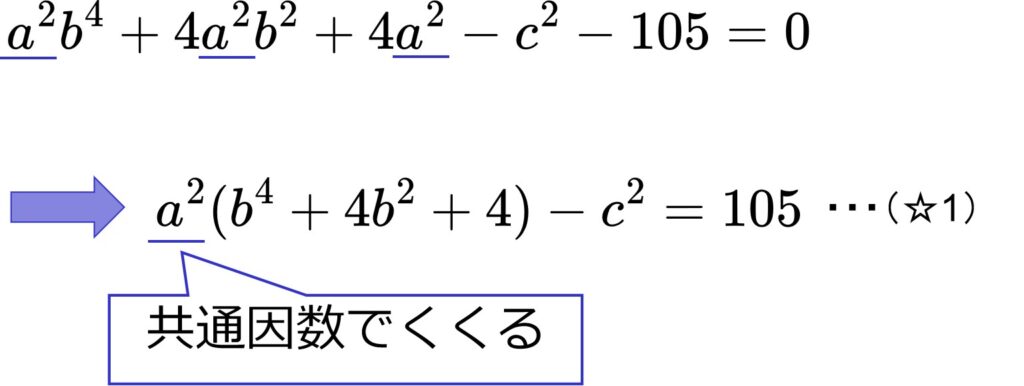
因数分解の定石その2-1:公式を使う
因数分解で次に考えることは、公式を使うこと。
必死におぼえた因数分解の公式を思い出し、「使えるものはないかな~?」と探します。

(☆1)をじーっと眺めますと……
\(a^2\)でくくったカッコ内!!
公式(ii)が!!!
使えるんです!!!!

なんだこのテンション
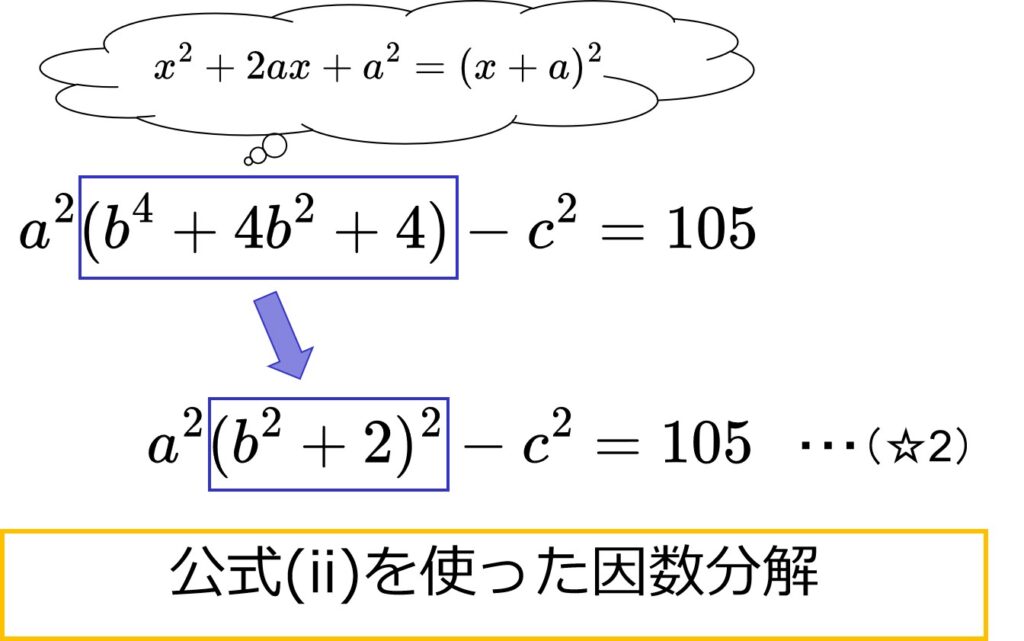
因数分解の定石その2-2:平方(2乗)の差に注目
さて、目標は【(A式)×(B式)=整数】の形を作り出すことでした。
(☆2)はまだこの形ではありません。
ということは、、、
さらに因数分解をする必要があります。

共通因数はムリってことで公式を使う
再び式をじーっと眺めます。
2乗の差に気づいてほしい。
公式(iv)を使ってさらに因数分解できます。
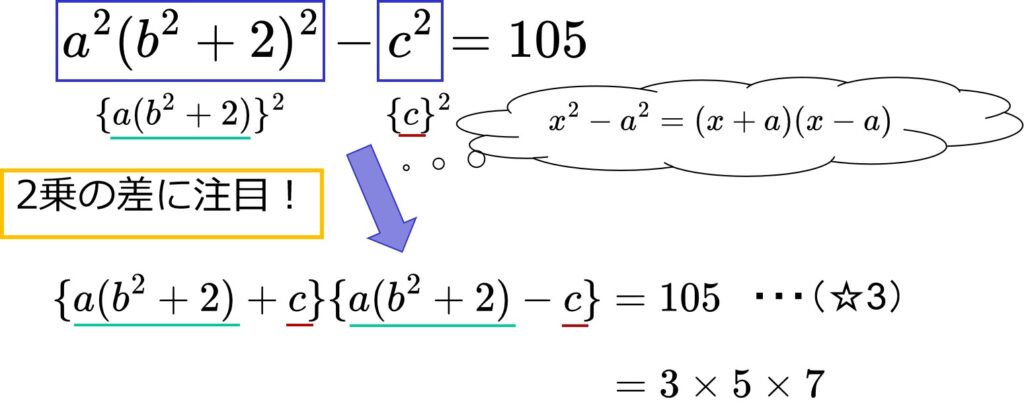

「(A式)×(B式)=整数」の形になりました
候補を書き出す:2つの{}は105の約数
A式&B式は105の約数です。
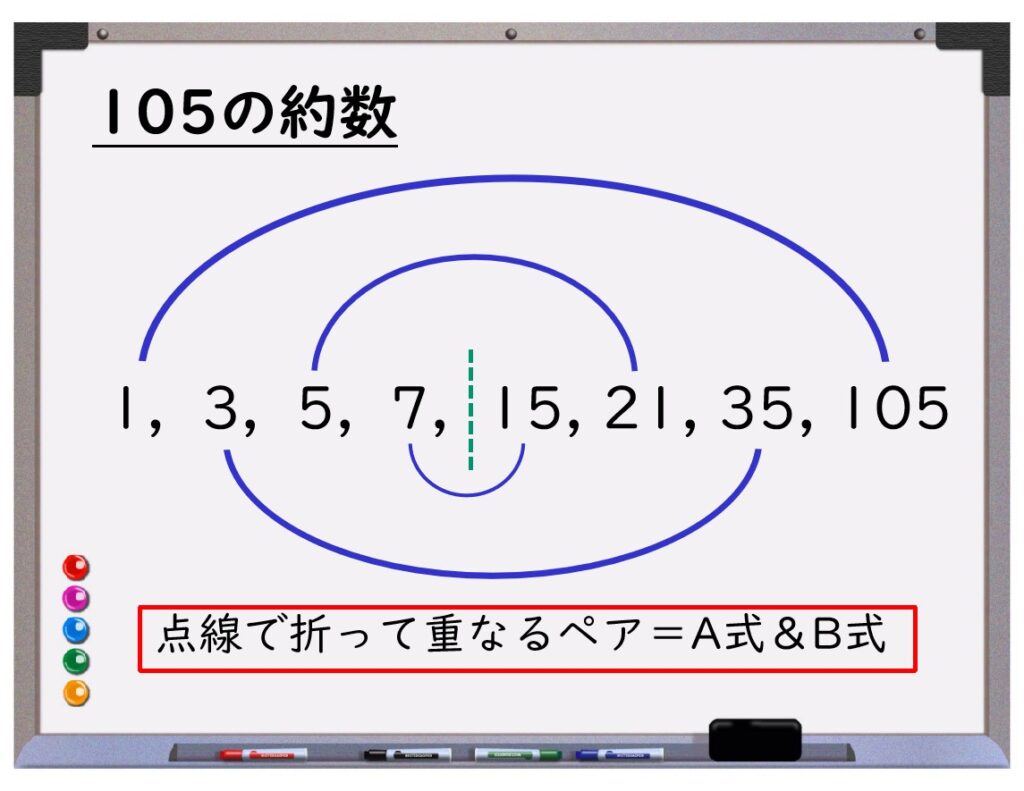
「A式 > B式」に注意すれば、A式&B式を次のように書き出せます。

\(c\)を足したもの(=A)の方が引いたもの(=B)より大きい
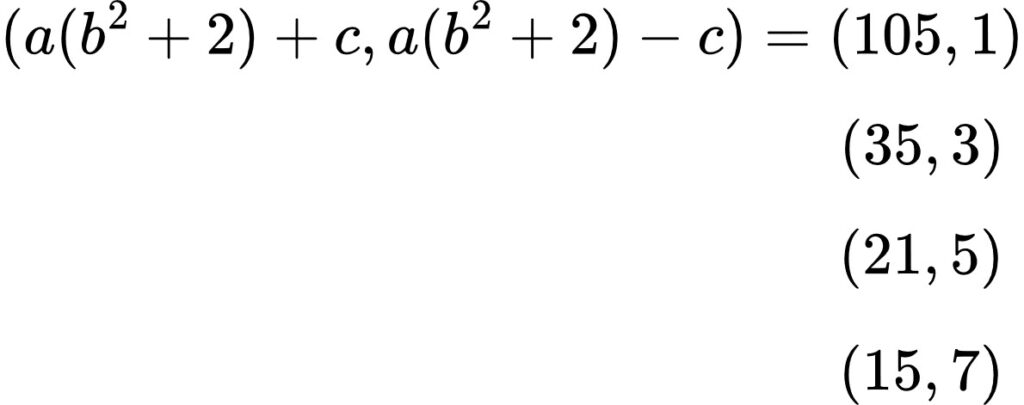
全パターンをしらみつぶし
各パターンそれぞれで、「A=~」と「B=~」を辺同士足し合わせます。(\(c\)を消去)
上から順に、\(a(b^2+2)=53, 19, 13, 11\)
いずれも素数なので、\(a=1\)
よって、\(b^2+2=53, 19, 13, 11\)
→\(b^2=51, 17, 11, 9\)
このうち、2乗を取り払って整数になるのは9だけ。
→\(b=3\)
このとき、(A式, B式)=(15, 7)
つまり、\(a(b^2+2)+c=15\)
→\(c=4\)
これより、\(a+b+c=1+3+4=8\)
以上より、2が正解です。
おわりに:整数には書き出し&しらみつぶし
お疲れ様でした!
整数問題には定番の解き方があります。
その一つが、約数を利用して解くやり方。
今回は、因数分解を使って【(A式)×(B式)=整数】の形を作って解く問題でした。
この形ができれば、あとは約数のペアを書き出してしらみつぶしできます。
【(A式)×(B式)=整数】を作って約数に持ち込む、という解き方はぜひ覚えてください。
整数問題には、このほかにも定番の解き方があります。
以下の記事も参考に。
「範囲→書き出し→しらみつぶし」の3ステップ↓
余りの問題の解き方↓
自動洗浄のトイレ行くと座ってないのに水流れるよね

これがVIP待遇ってやつ?
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!





コメント